1) Ознакомиться с общими положениями и с конструкцией экспериментального стенда.
2) При помощи строботахометра и латора установить число оборотов вентилятора n =1000 об/мин.
3) При отсутствии жиклера снять показания двух манометров: регистрирующего полное давление  , и статическое давление
, и статическое давление  . Результаты измерений занести в таблицу 10.2 (форма таблицы приведена ниже).
. Результаты измерений занести в таблицу 10.2 (форма таблицы приведена ниже).
4) Вычислить  по формуле (10.2), скорость воздуха
по формуле (10.2), скорость воздуха  в сечении 1-1 по формуле (10.3), расход воздуха
в сечении 1-1 по формуле (10.3), расход воздуха  в сечении 1-1 по формуле (10.4).
в сечении 1-1 по формуле (10.4).
5) Установить положение жиклера, с длиной окна В =15 мм, поддерживая число оборотов n =1000 об/мин.
6) Снять показания двух манометров  , и
, и  . Результаты измерений занести в таблицу 10.2.
. Результаты измерений занести в таблицу 10.2.
7) Воспользовавшись таблицей 10.1, вычислить  и выбрать соответствующее этому отношению значение
и выбрать соответствующее этому отношению значение  (при необходимости прибегнуть к интерполяции).
(при необходимости прибегнуть к интерполяции).
8) В соответствии с соотношением (10.7) вычислить коэффициент расхода µ при данной площади сечения отверстия жиклера.
9) По уравнению (10.6) определить значение расхода  в сечении 1-1.
в сечении 1-1.
10) Вычислить скорость истечения в отверстии жиклера по формуле
 (10.10)
(10.10)
где Sж – площадь отверстия жиклера, м2 (получить измерением).
11) Определить критерий А как отношение скорости истечения из отверстия жиклера к скорости звука (скорость звука в воздухе  = 300 м/с).
= 300 м/с).
 (10.11)
(10.11)
12) Убедиться в том, что величина А относительно мала.
13) Вычислить значение критерия Рейнольдса и дать заключение о режиме течения воздуха в отверстии жиклера. Критерий Рейнольдса определяется по формуле
 (10.12)
(10.12)
где  - кинематическая вязкость воздуха в нормальных условиях (м2/с), равная отношению динамической вязкости
- кинематическая вязкость воздуха в нормальных условиях (м2/с), равная отношению динамической вязкости  и плотности воздуха ρ в нормальных условиях (
и плотности воздуха ρ в нормальных условиях ( = 0.00102 кг/м·с, ρ =1.293 кг/м3); dэ – эквивалентный диаметр жиклера, то есть диаметр отверстия, имеющего ту же площадь, что и прямоугольное сечение жиклера в данном эксперименте.
= 0.00102 кг/м·с, ρ =1.293 кг/м3); dэ – эквивалентный диаметр жиклера, то есть диаметр отверстия, имеющего ту же площадь, что и прямоугольное сечение жиклера в данном эксперименте.
14) Вычислить  по формуле (10.8) в сечении 1-1,
по формуле (10.8) в сечении 1-1,  в сечении 1-1 по формуле (10.9) и полное давление
в сечении 1-1 по формуле (10.9) и полное давление  в сечении 1-1 при установке жиклера по формуле
в сечении 1-1 при установке жиклера по формуле
 (10.13)
(10.13)
15) Сравнить полученное значение с показаниями манометра  .
.
16) Вычислить относительное расхождение результатов по формуле
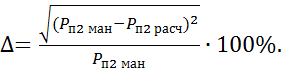 (10.14)
(10.14)
17) Установить длину окна жиклера В = 10 мм и повторить последовательность действий 6–14. Сделать выводы.
Таблица 10.2
| Без жиклера | С жиклером В =15 мм | С жиклером В =10 мм | |||
 , Па , Па
|  , Па , Па
|  , Па , Па
| 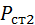 , Па , Па
|  , Па , Па
|  , Па , Па
|
Указание. Все расчеты производить в системе СИ и учитывать что, 1 мм в.ст.=10 Па.
Содержание отчета
1. Цель работы;
2. Краткие теоретические сведения;
3. Схема лабораторной установки (см. рис. 10.1);
4. Заполненную таблицу 10.2 с результатами измерений;
5. Расчетные формулы с подстановкой числовых данных и результаты расчетов;
6. Выводы по результатам исследований.
Контрольные вопросы
а) Чем отличаются уравнения энергетического баланса для идеальной и реальной жидкостей?
б) В каких случаях формулы для вычисления несжимаемой жидкости применимы в газодинамике?
в) Какие вы знаете виды потерь давлений при движении рабочей среды, и от чего они зависят?
г) Объясните энергетический смысл составляющих уравнения Бернулли.
д) Что такое вязкость рабочей среды? Чем она объясняется?
е) Что такое плотность рабочей среды? В чем принципиальное отличие плотности жидкости и газа?
11. Лабораторная работа № 11.
«Исследование закономерностей при непрямом гидравлическом ударе»
Цель работы: экспериментальное определение ударного давления при непрямом гидравлическом ударе и сравнение его с тем значением, которое вычисляется на основе теоретических рассуждений.
Содержание работы
1. Ознакомление с теоретической частью работы.
2.Ознакомление с элементной базой лабораторного стенда.
3. Составление гидравлической схемы экспериментального стенда.
4. Снятие рабочих характеристик.
5. Вычисление по теоретическим формулам скорости ударной волны и ударного давления при прямом гидравлическом ударе, сделать промежуточные выводы.
7. Вычисление погрешности аналитического расчета прямого и непрямого гидравлического удара относительно экспериментальных значений.
8. Формулировка выводов по работе.
Теоретический раздел
Гидравлическим ударом называется повышение или понижение гидромеханического давления в трубопроводе, вызванное изменением во времени (в каком-либо сечении трубопровода) средней скорости движения. Явление гидравлического удара обусловливается инерцией той массы жидкости, заключенной в трубопроводе, скорость которой изменяется во времени. Гидравлический удар в трубопроводе может достигать большой силы, которая способна привести к разрыву трубопроводов. Собственно и изучение гидравлического удара началось в связи с частыми авариями на новых линиях Московского водопровода, построенных в конце 19 века. Причины аварий было поручено исследовать ученому Жуковскому, который и разработал теорию гидравлического удара.
По Жуковскому, при быстром закрытии задвижки в трубопроводе скорость движения воды в нем уменьшается до нуля и происходит переход кинетической энергии потока в потенциальную, что приводит к повышению давления. Чем больше длина трубопровода, тем больше в нем масса жидкости и величина кинетической энергии, и тем больше будет повышение давления.
Однако эти рассуждения справедливы, если полагать, что жидкость сжимаема, и гидравлический удар следствие этого сжатия. Обычно, при установившихся течениях при сравнительно невысоких давлениях пренебрегают сжимаемостью капельных жидкостей, что для большинства задач гидравлики не вносит ощутимой погрешности. Но пренебрежение сжимаемостью не позволяет объяснить механизма распространения возмущений давления в жидкой среде. В абсолютно несжимаемой среде скорость распространения возмущений теоретически бесконечна. В реальных же средах она равна скорости распространения звука. В теории Жуковского выдвинуто предположение, что режим течения жидкости при гидравлическом ударе неустановившийся, а также то, что на сжимаемость транспортируемой по системе жидкости накладываются упругости стенок трубопровода, которые также не является абсолютно жесткими.
В теории гидравлического удара введено понятие «фаза гидроудара».
Фаза гидроудара это время распространения положительного и отрицательного давления при мгновенном закрытии задвижки, перекрывающей сечение трубопровода. Процесс распространения давлений – волновой и сопровождается изменением направления скорости ударной волны от задвижки к баку и затем от бака вновь к задвижке. Фаза гидроудара может состоять из условно принятых восьми частей – столько раз волна давления меняет свое направление, отражаясь от заслонки, допустим слева, и от условно неподвижного объема жидкости в баке на входе в трубопровод, по которому течет жидкость, справа от заслонки. При этом меняется также диаметр сечения трубопровода вследствие упругости металла стенок. Он сначала увеличивается от положительного давления на стенки изнутри, затем уменьшается от отрицательного давления. Скорость распространения ударной волны в капельных жидкостях достаточно высока и сравнима по значению со скорость звука в этих жидкостях, для воды – 1425 м/с.
Если время закрытия задвижки tз меньше фазы удара, то такой гидроудар называется прямым, если время закрытия задвижки больше фазы удара, то имеет место непрямой удар. Вообще кинетическое движение жидкости, его потока при перетекании жидкости из одного установившегося объема в другой начинается после времени прохождения фазы гидравлического удара между этими объемами.
Фаза гидроудара может быть подсчитана по формуле:
 , (11.1)
, (11.1)
где  – длина трубопровода, м (
– длина трубопровода, м ( м) м; Сv – скорость ударной волны, м/с.
м) м; Сv – скорость ударной волны, м/с.
В соответствии с теорией прямого гидравлического удара, повышение давления перед заслонкой определяется по формуле Жуковского [1].
 (11.2)
(11.2)
где ρ – плотность жидкости, кг/м3 (для воды  кг/м3);
кг/м3); 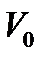 – скорость жидкости в трубе до гидравлического удара, м/с.
– скорость жидкости в трубе до гидравлического удара, м/с.
Скорость распространения ударной волны для воды определяется по следующей формуле:
 (11.3)
(11.3)
где  — модуль упругости жидкости, Па (для воды
— модуль упругости жидкости, Па (для воды 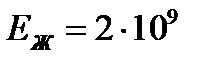 Па);
Па);  — модуль упругости металла трубы, Па (для стали
— модуль упругости металла трубы, Па (для стали  Па);
Па);  — скорость распространения звука, м/с (скорость распространения звука в воде
— скорость распространения звука, м/с (скорость распространения звука в воде 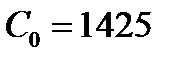 м/с); δ — толщина стенки трубы, м (
м/с); δ — толщина стенки трубы, м (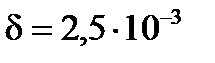 м);
м);  — внутренний диаметр трубы, м (
— внутренний диаметр трубы, м ( м).
м).







