1) Ознакомиться с конструкцией установки и принципом ее работы.
2) Экспериментально установить зависимость скорости V воздуха в вентиляторе в зависимости от частоты вращения n колеса, а также зависимость мощности вентилятора 
от величины n.
3) Изменяя частоту вращения ротора n, для пяти разных скоростей его вращения определить полного 
и статического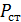 
давление (nmax брать равным 8000 об/мин). Для измерения полного и статического давление потока воздуха устанавливаются внутрь воздухопровода вентилятора вводятся пневмометрическая трубки, которые подключаются к водяным манометрам. При водяных манометров измеряется статическое и полное давление. Поскольку
, (9.7)
то
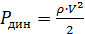, (9.8)
где ρ – плотность воздуха (кг/м3);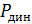 
– динамическое давление (Па).
Давление, уравновешиваемое высотой водяного столба в h=1мм (1 мм в.ст.), соответствует давлению Р = 9,81 Па ≈ 10 Па.
4) Определить скорость воздушного потока V, расход (производительность) вентилятора Q и мощность для тех же скоростей вращения ротора.
5) Определить сечение f трубопровода (воздухопровода). Принимать его как прямоугольник и измерять с помощью линейки.
6) Результаты расчетов и измерений занести в таблицу 9.1.
7) Установить жиклер на выходное отверстие центробежного вентилятора и повторить последовательность п.п. 3–6. Результаты расчетов и измерений занести в таблицу 9.2 аналогичную таблице 9.1. Длина окна жиклера В = 10 мм.
8) Представить в виде графиков зависимости скорости воздушного потока V, расхода Q, мощности N и динамического давления 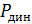от частоты вращения ротора центробежного вентилятора n, т.е. V=f(n), Q=f(n), =f(n), 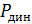=f(n) для двух различных проходных сечений воздухопровода центробежного вентилятора.
9) На основании исследования сделать соответствующие выводы.
Таблица 9.1
| № п/п | n, об/мин | 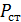, Па
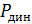| , Па
| , Па
| V, м/с | Q, м3/с | , Вт
|
| … | |||||||
Содержание отчета
1. Цель работы;
2. Краткие теоретические сведения;
3. Электрическая схема управления центробежным вентилятором (см. рис. 9.4) и его конструкция (см. рис. 9.1);
4. Заполненные таблицы 9.1 и 9.2 результатами измерений и вычислений;
5. Расчетные формулы с подстановкой числовых данных и результаты расчетов;
6. Графические зависимости V=f(n), Q=f(n), =f(n), 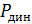=f(n) при различных скоростях вращения ротора и для двух различных проходных сечений воздухопровода центробежного вентилятора;
7. Выводы по результатам исследований.
Библиографический список
1. Калиушин Н.П. Вентиляторные установки. – изд. 6. – М.: Высшая школа, 1967. – с.136
2. Вильнер Я.М. и др. Справочное пособие по гидравлике, гидромашинам и гидропроводам. – 2-е изд. – М.: Высшая школа, 1985. – с.381
10. Лабораторная работа №10.
«экспериментальная Проверка уравнения Бернулли в воздушном потоке центробежного вентилятора»
Цель работы: Подтвердить экспериментально равенство энергетического баланса (уравнение Бернулли) на примере исследования истечения потока воздуха через диффузор центробежного вентилятора при незначительных перепадах давлений в местных сопротивлениях.
Теоретический раздел
Общее положение
В пневмоприводах энергопередающей средой является газ, в качестве которого выступает обычно сжатый воздух. При своем течении газ протекает через различные приборы, механизмы, детали, устройства и пневмомагистрали, которые классифицируются как местные сопротивления. Кроме местных сопротивлений существуют сопротивления по длине трубопровода, если он имеет круглое сечение. При своем течении по трубопроводу и через местные сопротивлениям газ теряет часть своей энергии, которая определяется, в основном, падением давления и сокращением расхода, однако, согласно закону сохранения энергии энергетический баланс должен сохраняться.
В зависимости от формы и размеров местных сопротивлений, величин давлений, режима течения, уравнения энергетического баланса для газов могут записываться в различных формах, так как совершающий работу газ может существовать, как известно, в нескольких термодинамических состояниях.
Если перепад давлений в местном сопротивлении невелик и числа М потока малы (М=v/a – критерий подобия, выражающейся как отношение скорости потока к скорости звука в том же месте), то можно вести расчеты потерь давлений и расхода в сопротивлениях, пользуясь уравнениями, выведенными для несжимаемой жидкости.
Рисунок 10.1 – Схема лабораторной установки
Рассмотрим схему стенда, предлагаемого для испытаний (см. рис. 10.1).
В приведенной схеме в качестве источника энергии используется центробежный вентилятор. Данная машина относится к классу динамических машин, обеспечивающих достаточно высокие расходы, но незначительные напоры, поэтому при отношении А/В =1,3÷2 и числе оборотов n =1000об/мин, понятия газа наблюдаться не будет, а следовательно, в соответствии с приведенным выше уравнением, состояние газа описывается уравнениями несжимаемой жидкости.
В приведенной схеме сопло №1 установлено коаксиально потоку воздуха и воспринимает полное давление РП ,, регистрируемое водяным манометром. Сопло №2 установлено перпендикулярно потоку и воспринимает статическое давление РСТ, которое также регистрируется вторым водяным манометром, причем, поскольку участок диффузора за соплом 2 короткий, неизбежно возникновение эжекторного эффекта, то есть давление в этом сопле будет меньше атмосферного, (отрицательным), что и будет зарегистрировано манометром.
Если рассматривать данную схему без сменного жиклера, то есть без сопротивления препятствующего потоку воздуха, то справедливо следующее уравнение Бернулли для сечения 1-1.
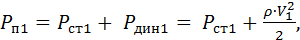(10.1)
где 
– динамическое давление в сечении 1-1, равное произведению плотности r воздуха при нормальных условиях и квадрату скорости воздуха 
в том же сечении, деленному на два. С учетом того, что 
отрицательное, что уменьшает полное давление в сечении, динамическое давление можно вычислить как разность измеренного полного и статического давлений, то есть
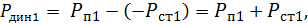(10.2)
Из равенства (10.1, 10.2) можно определить скорость воздуха в сечении 1-1,
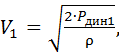(10.3)
где r – плотность воздуха в нормальных условиях (r = 1,293 кг/м3); 1мм вод. столба = 10Па.
При этом расход воздуха, протекающий через поперечное сечение 1-1, можно подсчитать по формуле:
(10.4)
где S1 – площадь поперечного сечения, в данном случае прямоугольника со сторонами А = 20 мм и В = 10 мм.
При установке жиклера, который является местным сопротивлением, соотношение давлений в сечении 1-1 изменится.
Задачей данного исследования является доказательство того, что и в этой ситуации сохранится энергетический баланс, который описывается уравнением (10.1).
Иначе говоря, следует доказать, что измеренное в иных условиях статическое давление в сечении 1-1 
и вычисленное косвенным образом динамическое давление 
в сумме должны соответствовать замеренному манометром значению 
.
Проанализируем ситуацию. Местное сопротивление в виде жиклера создаст препятствие прохождению воздуха наружу, что неизбежно должно сказаться на увеличении статического давления . Вместе с тем, должен сократиться расход воздуха через жиклер в сечении 1-1 – 
по отношению к первоначальному расходу 
, что приведет к снижению скорости v2 потока в сечении 1-1, и к снижению динамического давления .
Расход непосредственным измерением на данном стенде получить невозможно, поэтому следует прибегнуть к теоретическим данным.
При истечении воздуха через диффузор без жиклера объемный расход воздуха , определенный по формуле (10.4), близок к теоретическому. При установке жиклера, объемный расход воздуха меньше теоретического и кратен коэффициенту m, который называется коэффициент расхода и равен отношению действительного расхода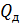 
к теоретическому – 
.
В настоящей схеме можно полагать, что:
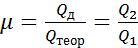, (10.5)
тогда расход равен:
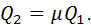(10.6)
Коэффициент m зависит от конкретного местного сопротивления, режима истечения и обычно, находится экспериментально. В некоторых случаях он может быть найден аналитически. Коэффициент расхода для жиклеров находят по формуле
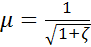, (10.7)
где 
– коэффициент потерь давления в местном сопротивлении, в данном случае в жиклере.
Значения коэффициента 
в основном определяются геометрическими размерами и видом местного сопротивления, рассчитываются по эмпирическим формулам, но чаще их значения получают эмпирически и задают в виде таблиц в специальных справочниках. Ниже приведена выборка из таблицы справочника для случая, аналогичного настоящей лабораторной работы.
Таблица 10.1
| Тип жиклера
Отверстие с острыми кромками
| |||||
| 0,2 | 0,4 | 0,6 | 0,8 | 0,9 | |
|
| 2,01 | 1,83 | 1,66 | 1,26 | 1,03 | 0,88 |
Здесь F0 и F1 – соответственно площади сечений отверстия жиклера и площади сечения воздуховода до жиклера.
Выбрав по таблице 10.1 соответствующее значение , можно, в соответствии с формулой (10.7), рассчитать коэффициент расхода µ и вычислить значение расхода по формуле (10.6), а также значение скорости 
в сечении 1-1 по формуле
. (10.8)
Зная значение скорости в сечении 1-1, можно рассчитать динамическое давление в сечении 1-1 при установленном жиклере
. (10.9)
Следующим этапом является вычисление как суммы замеренного статистического давления и вычисленного по формуле (10.9) динамического давления и сравнение результата с показаниями манометра 
.. Результаты должны совпадать, естественно с определенной погрешностью, укладывающуюся в пределах допустимой. Совпадение результатов доказывает соотношение составляющих энергетического баланса в соответствии с уравнением Бернулли и раскрывает механизм поведения потока воздуха в исследуемом объекте.
Программа исследования
· Ознакомиться с конструкцией экспериментального стенда.
· Снятие необходимых характеристик для расчета без использования жиклера.
· Снятие характеристик, при установленном жиклере.
· Выполнение расчетов.
· Сопоставление расчетных и экспериментальных данных.
· Проведение статической обработки данных эксперимента.
