Лабораторный стенд состоит из бака 1, стеклянной прозрачной трубки 4, на конце которой установлен кран K8, емкость 3 с окрашенной водой (марганец) из которой окрашенная струйка вытекает по тонкой трубке 5.
Расход воды определяется объемным способом: 
, а средняя скорость 
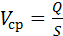, где S – площадь сечения трубопровода, W – объем воды, поступившей в сливной бак 2 за время Т.
Рисунок 2.1 – Схема лабораторного стенда
Порядок выполнения экспериментальных исследований
1) Закрыть кран К2 и К7, а затем открыть К1 и наполнить напорный бак 1 водой, контролируя ее уровень по водомерной трубке. Открыть кран К6 и слить воду из мерного бака (если она там есть).
2) Закрыть кран К6. Открыть краны К7, К8, К9 и с помощью крана К8 в стеклянной трубке 4 создать ламинарный режим движения жидкости (окрашенная струя жидкости, которая вытекает из сливной магистрали 5, не смешивается с потоком воды);
3) Измерить температуру воды t и отрезок времени Т, за которой наполняется сливной бак 2 (или некоторая его часть);
4) С помощью крана К8 создать турбулентный режим и произвести такие же измерения как в п.3;
5) Определить среднюю скорость движения жидкости (Vср), расход (Q), а также число Рейнольдса для каждого режима течения жидкости. Все результаты измерений и вычислений записать в таблицу 2.2.
Таблица 2.2
| Наблюдаемый режим движения | Объем воды в мерном баке, W (м3) | Время наполнения бака, T (с) | Средняя скорость, V (м/с) | Расход, Q (м3/с) | Число Рейнольдса, Re |
| Ламинарный | |||||
| Турбулентный |
Содержание отчета
1. Цель работы;
2. Краткие теоретические сведения;
3. Схема лабораторного стенда (см. рис. 2.1);
4. Заполненную таблицу 2.2 результатами измерений и вычислений;
5. Расчетные формулы с подстановкой числовых данных и результаты расчетов;
6. Выводы по результатам исследований.
Контрольные вопросы
а) При каких условиях может существовать ламинарный и турбулентный режимы движения жидкости?
б) Как зависит значение «критического» числа Рейнольдса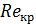 
от формы и свойств трубы, по которой протекает жидкость?
в) Как изменяется кинематическая вязкость воды при изменении температуры?
г) Какой режим движения жидкости чаще встречается в гидросистемах? Почему?
Библиографический список
1. Гидравлика, гидромашины, гидроприводы / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. - М: Машиностроение, 1982. - 423с.
2. А.А. Угинчус. Гидравлика и гидравлические машины - изд.4, перераб. и доп. -Изд-во Харьковского ун-та, 1970.
3. Большаков В.А. и др. Справочник по гидравлике. - К.: Вища школа, 1984. – 343 с.
4. Вакина Б.В.. Денисенко И.Д., Столяров А.Л. Машиностроительная гидравлика. Примеры расчетов. - К: Вища школа, 1987. - 208 с.
3. Лабораторная работа №3.
«Экспериментальное исследование
коэффициента гидравлического трения»
Цели работы: экспериментально определить коэффициент гидравлического трения λ при разных значениях числа Рейнольдса и сравнить его со значениями, вычисленными по эмпирическим формулам.
Теоретический раздел
Основные положения
Как показали многочисленные эксперименты и большой практический опыт, потери по длине зависят от длины трубы l и диаметра d, шероховатости ее стенок, средней скорости V и кинематической вязкости ν жидкости.
Они определяются по формуле Дарси-Вейсбаха:
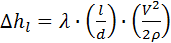, (3.1)
где λ – коэффициент гидравлического трения (коэффициент Дарси), который надо определить при выполнении этой лабораторной работы.
Принимая во внимание, что труба лабораторного стенда горизонтальная и ее диаметр не меняется, то есть средняя скорость V = const, а также на рабочем участке нет никаких местных сопротивлений, из уравнения Бернулли, относительно площади сравнения О-О для поперечных сечений 1-1 и 2-2, придем к выводу, что
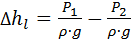. (3.2)
В таблице 3.1 приведены значения средней высоты выступов шероховатости (∆) внутренней поверхности некоторых труб.
Таблица 3.1 – Средняя высота выступов шероховатости внутренней поверхности трубы
| Трубы: | ∆, мм |
| 1. Стальные бесшовные: а) новые чистые; б) старые, находящиеся в эксплуатации. | 0,03…..0,05 0,06….0,15 |
| 2. Стальные сварные: а) новые и чистые; б) умеренно ржавые; в) старые ржавые. | 0,04…0,06 0,08…0,15 0,2…0,7 |
| 3. Из цветных металлов | 0,005 |
| 4. Гибкие рукава | 0,03 |
Из формулы 3.1 можно получить зависимость для определения λ с помощью эксперимента:
(3.3)
Значения коэффициента λ, которые будут получены по формуле 3.2, сравним со значениями, которые будут вычислены по одной из приведенных далее формул. При ламинарном режиме справедлива формула:
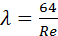(3.4)
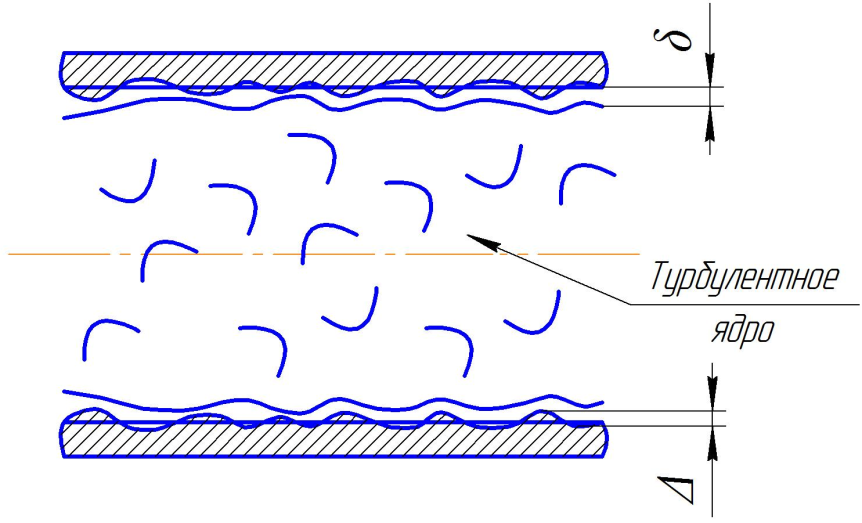
Рисунок 3.1 – Турбулентное ядро
На основе исследований уставлена такая структура турбулентного потока: 1) тонкая ламинарная пленка около стенок трубы; 2) переходный слой; 3) турбулентное ядро, занимающее всю центральную часть потока (см. рис. 3.1). Ламинарная пленка полностью или частично покрывает элементы шероховатости на внутренней поверхности стенок трубы, около которых постоянно возникают завихрения, переходящие в ядро потока, где они постепенно разделяются на меньшие завихрения. Кинетическая энергия мельчайших завихрений под действием сил внутреннего трения переходит в теплоту. Так можно объяснить процесс расхода энергии на преодоление трения (потерь по длине) при турбулентном движении жидкости.
Толщина ламинарной пленки δ зависит от скорости течения потока – при увеличении скорости она уменьшается.
В зависимости от соотношения высоты выступов шероховатости ∆ (см. табл. 3.1) и толщины ламинарной пленки δ при турбулентном режиме движении жидкости выделяют три зоны гидравлических сопротивлений:
1) при δ >∆, то есть выступы шероховатостей полностью покрыты ламинарной пленкой или при
2300< Re <20 d/ ∆, (3.5)
имеет место гладкая зона гидравлических сопротивлений, для которой справедлива формула Блазиуса:
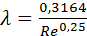(3.6)
2) при δ =∆ или при
20 d/ ∆< Re <500 d/ ∆, (3.7)
имеет место переходная зона гидравлических сопротивлений, в которой λ вычисляется с помощью формулы Альтшуля:
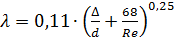(3.8)
3) при δ <∆ или при
Re >500 d/ ∆ (3.9)
наступает квадратичная зона гидравлических сопротивлений, для которой, с помощью формулы Шифринсона, получим:
(3.10)
Лабораторный стенд (см. рис. 3.2) состоит из напорного бака 1, трубы 3 неизменного поперечного сечения и сливного бака 2. В начале и в конце рабочей поверхности длиной L установлены открытые пьезометры.
Рисунок 3.2 – Схема лабораторного стенда
