Порядок выполнения экспериментальных исследований

Севастопольский национальный технический университет

 

 

«Основы гидрогазодинамики»

 

Методические указания
к выполнению лабораторных работ №1-11
по дисциплине
«Гидрогазодинамика»

для студентов направления
15.03.04 – «Автоматизация технологических процессов и производств»
всех форм обучения

 

Севастополь

«Основы гидрогазодинамики». Методические указания к выполнению лабораторных работ по дисциплине «Гидрогазодинамикиа» для студентов направления 15.03.04 – «Автоматизация технологических процессов и производств / Сост.: Федоренко С.Н., Вожжов А.А., Головин В.И., Осипов К.Н. – Севастополь: Изд-во СевНТУ, 2015. – 52 с.

 

 

Цель: настоящие методические указания предназначены для оказания помощи студентам при выполнении лабораторных работ. В методических указаниях изложены методики расчета и определения различных гидравлических коэффициентов, режимов течения жидкости, исследование основных законов гидравлики и газодинамики.

Методические указания рассмотрены и утверждены на заседании кафедры «Автоматзация технологических процессов и производств»

(протокол №___ от «___» __________ 2014 г.)

 

Допущено учебно-методическим центром СевНТУ в качестве методических указаний

 

Рецензент:

Поливцев В.П., к.т.н, доцент кафедры «Автоматзация технологических процессов и производств».

 

СОДЕРЖАНИЕ

1. Лабораторная работа № 1. «Уравнение Бернулли для установившегося потока вязкой жидкости». 4

2. Лабораторная работа №2. «Исследование режимов движения жидкости». 8

3. Лабораторная работа №3. «Экспериментальное исследование коэффициента гидравлического трения». 11

4. Лабораторная работа №4. «Экспериментальное исследование коэффициентов местных гидравлических сопротивлений». 15

5. Лабораторная работа №5. «Определение статической характеристики усилителя типа сопло-заслонка». 18

6. Лабораторная работа №6. «Исследование автоматизированного гидравлического привода». 23

7. Лабораторная работа №7. «Исследование основных характеристик гидравлического шестеренчатого насоса». 27

8. Лабораторная работа №8. «Исследование процесса преобразования энергии сжатого воздуха в механическую работу на примере линейного пневматического привода». 31

9. Лабораторная работа №9. «Исследование характеристик динамического воздушного насоса». 37

10. Лабораторная работа №10. «экспериментальная Проверка уравнения Бернулли в воздушном потоке центробежного вентилятора». 42

11. Лабораторная работа № 11. «Исследование закономерностей при непрямом гидравлическом ударе». 47

 

 

1. Лабораторная работа № 1.
«Уравнение Бернулли для установившегося
потока вязкой жидкости»

 

 

Цель работы: Теоретически и экспериментально определить величины, входящие как слагаемые в уравнение Д. Бернулли.

 

Теоретический раздел

Основные положения

Уравнение Бернулли – основное уравнение гидравлики, выражает закон сохранения энергии установившегося потока жидкости в поле сил земного тяготения и имеет вид:

, (1.1)

где α – коэффициент кинетической энергии или коэффициент Кориолиса
(α = 1 – турбулентный поток, α = 2 – ламинарный поток); V₁ и V₂ – средняя скорость потока соответственно в первом и во втором сечении трубопровода, которые находятся один от другого на расстоянии L, м/с (см. рис. 1.1); ρ – плотность жидкости (кг/м³); g – ускорение свободного падения; P₁ и P₂ – абсолютное (полное) давление в первом и во втором сечении трубопровода (Па); z₁ и z₂ –расстояния от произвольной горизонтальной (нулевой) плоскости сравнения до центров поперечных сечений (м); h_w – величина потерь удельной энергии на преодоление гидравлических сопротивлений (м).

Таким образом, сумма удельной потенциальной, кинетической и затраченной энергии вдоль потока есть величина постоянная.

Удельную энергию положения (геометрическую высоту) z можно измерить, как расстояние по вертикали от горизонтальной плоскости сравнения до центра сечения. Удельную потенциальную энергию давления – высоту давления можно измерить с помощью пьезометрической трубки. Удельную кинетическую энергию – скоростную высоту можно измерить, как разницу высот в гидродинамической и пьезометрической трубках.

 

 

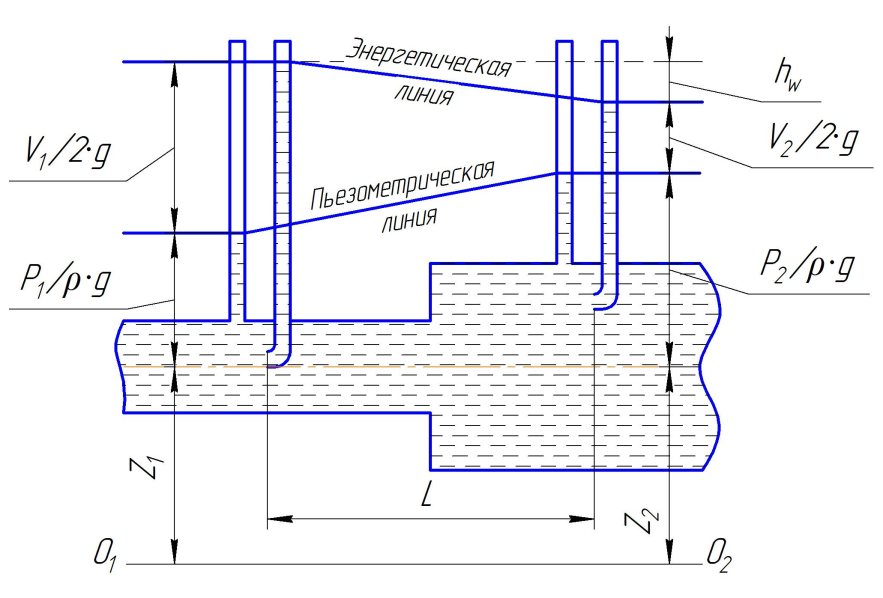
Рисунок 1.1 – Участок гидравлического стенда с пьезометрическими и
гидродинамическими трубками

 

Линия, которая проходит через уровни жидкости в пьезометрических трубках и показывает, как изменяется удельная потенциальная энергия вдоль потока, называется пьезометрической.

Линия, которая соединяет уровни жидкости в гидродинамических трубках и показывает, как изменяется полная удельная энергия вдоль потока, называется энергетической (напорной) линией. Поскольку во время движения жидкости часть ее энергии затрачивается на преодоление сил трения и различные местные сопротивления, напорная линия постепенно снижается. Пьезометрическая линия на отдельных участках трубопровода может повышаться. Это может происходить тогда, когда вследствие увеличения диаметра трубы скорость, а также и удельная кинетическая энергия уменьшаются.

Интенсивность потерь энергии измеряется гидравлическим уклоном i_z:

, (1.2)

где L – расстояние между первым и вторым сечениями трубы.

При равномерном движении жидкости в трубе неизменного поперечного сечения (V₁=V₂) гидравлический уклон равен пьезометрическому:

, (1.3)

Лабораторный стенд, схема которого приведена на рисунке 1.2., состоит из напорного бака 1, в котором уровень воды поддерживается постоянным (излишек воды вытекает сквозь специальное отверстие в канализацию) и трубопровода 3 и 4. Диаметр трубопровода 4 изменяется вдоль потока течения жидкости. Из трубопровода 4 вода попадает в мерный бак 2 (сливной бак), с помощью которого можно определить расход (, где – объем жидкости, поступившей в бак за время ).

Во всех характерных сечениях трубопровода (поз. 1-12 на рисунке 1.2.) установлены пьезометрические и гидродинамические трубки.

Рисунок 1.2 – Схема лабораторного гидравлического стенда

 

Программа исследования

В ходе выполнения работы студент должен с помощью пьезометрических и гидродинамических трубок определить удельную потенциальную 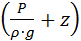и кинетическую энергии в характерных сечениях трубы и на основе этих измерений построить пьезометрическую и напорную (энергетическую) линии.

проверить такие теоретические положения: изменение удельной кинетической энергии приводит к изменению удельной потенциальной энергии; во время движения жидкости ее полная энергия постепенно уменьшается.

Порядок выполнения экспериментальных исследований

1) Закрыть кран К₄ и К₅, а затем открыть К₁ и наполнить напорный бак 1 водой, контролируя ее уровень по водомерной трубке. Открыть кран К₆ и слить воду из мерного бака (если она там есть).

2) Закрыть кран К₆, открыть кран К₄ в конце трубы переменного сечения и с помощью крана К₁ добиться, чтобы уровень воды в напорном баке не изменялся.

3) Записать в колонки 2 и 3таблицы 1.1 показания пьезометрических и гидродинамических трубок в каждом сечении.

4) Подсчитать значения удельной энергии и внести их в колонки 4,5 и 6 таблицы 1.1.

5) Определить потери энергии на каждом сечении и записать в колонку 7 таблицы 1.1.

6) По данным измерений построить пьезометрическую и энергетическую линии. На основе этой диаграммы сделать выводы о характере изменений каждого вида удельной энергии и суммарной удельной энергии .

7) Кроме того, определить величину расхода воды (Q) за время проведения исследований. Для этого необходимо с помощью мерного бака и секундомера определить объем воды (W), который вытек из трубопровода за некоторый отрезок времени (T) и зафиксировать отчете.

Таблица 1.1

Номер сечения	Показания трубок	Удельная энергия (см)
Пьезо- метрии- ческой	Гидро- динами- ческой	Потен- циальная	Кинема- тическая	Полная	Потери
…

 

 

Содержание отчета

Отчет о выполнении лабораторной работы, оформленный в соответствии с действующими стандартами Украины для текстовых документов должен содержать:

1. Цель работы;

2. Краткие теоретические сведения;

3. Схема лабораторного стенда (см. рис. 1.1);

4. Заполненную таблицу 1.1 результатами измерений и вычислений;

5. Расчетные формулы с подстановкой числовых данных и результаты расчетов;

6. Графические изображения пьезометрической и энергетической линии;

7. Вывод по результатам исследований. В выводе необходимо отразить подтверждаются ли теоретические положения, отмеченные в поставленных задачах к лабораторной работе или нет.

 

Контрольные вопросы

а) Каков физический смысл величин, входящих в уравнения Бернулли?

б) Какие существуют ограничения на применение уравнения Бернулли?

в) К каким выражениям приводятся уравнения Бернулли в случаях:
– неподвижной жидкости?
– равномерного движения в горизонтальном трубопроводе?
– истечения жидкости из бака через маленькое круглое отверстие?

г) Каковы основные причины возникновения потерь напора при движении вязкой жидкости? Чем отличаются уравнения Бернулли для идеальной и реальной жидкости?

д) Каков геометрический и физический смысл понятий: геодезический, пьезометрический, гидравлический уклон?

е) Может ли быть отрицательным гидравлический уклон? Почему?

ж) Может ли быть отрицательным пьезометрический уклон? Почему?

 

Библиографический список

1. Гидравлика, гидромашины, гидроприводы / Т.М. Башта. С.С. Руднев, Б.Б. Некрасов и.др. М: Машиностроение, 1982. -423с.

2. Угинчус А.А. Гидравлика и гидравлические машины - изд.4, перераб. и доп. - Изд-во Харьковского ун-та, 1970.

3. Большаков В.А. и др. Справочник по гидравлике. - К.: Вища школа, 1984, - 343 с.

4. Вакина Б.В., Денисенко И.Д., Столяров А.Л. Машиностроительная гидравлика. Примеры расчетов. - К: Вища школа, 1987. - 208 с.

 

2. Лабораторная работа №2.
«Исследование РежимОВ движения жидкости»

 

Цель работы: произвести наблюдение ламинарного и турбулентного режимов движения жидкости и проверить условия их существования.

 

Теоретический раздел

Основные положения

Впервые режимы движения подробно исследовал английский физик Осборн Рейнольдс. Было установлено, что при малых средних по сечению скоростях потока жидкости в трубе наблюдается ламинарный режим движения, когда слои жидкости не смешиваются, а передвигаются вдоль трубы по прямолинейным траекториям. Когда средняя скорость V_ср приближается к некоторому критическому значению V_кр, слои жидкости начинают совершать колебательные движения, пульсировать, закручиваться. При дальнейшем увеличении средней скорости поток становится еще не стабильнее, в нем возникают завихрения. При V_ср = V_кр возникает турбулентный режим движения и слои жидкости интенсивно смешиваются между собой.

Ламинарный режим встречается достаточно редко – при течении очень вязких жидкостей или при очень малых скоростях движения. В большинстве случаев на практике наблюдается турбулентный режим движения. Исследованиями Рейнольдса доказано, что переход от ламинарного режима к турбулентному и наоборот происходит при некоторых значениях безразмерного параметра, названного позже числом Рейнольдса, которое определяется следующим образом:

, (2.1)

где V_ср – средняя скорость течения жидкости, d – диаметр трубопровода, ν – кинематическая вязкость жидкости.

Эти значения называются «критическими» числами Рейнольдса 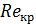. При наблюдается ламинарный режим движения, при – турбулентный. Так для труб круглого поперечного сечения , для гибких рукавов , для окон цилиндрического золотника , для плоских и конусных клапанов . Значение кинематической вязкости воды представлены в таблице 2.1.

 

Таблица 2.1 – Кинематическая вязкость воды при различных значениях температуры

Температура воды, t (°C)
Кинематическая вязкость, ν (мм2/с)	1,57	1,47	1,39	1,31	1,24	1,18	1,12	1,06	1,01