«Динамика несвободной системы с двумя степенями свободы»
Схемы конструкций представлены на рис. 6.2. Исходные данные приведены в табл. 6.1 (основные размеры, массы звеньев, жесткости пружин и пр.), начальные условия обобщенных координат и обобщенных скоростей – в табл. 6.2. Конкретно задача сформулирована в соответствии с номером варианта на рис. 6.2.
| Т а б л и ц а 6.1 Рекомендуемые значения характерных физических величин | |||||||||||||
| Физическая величина | Номер варианта схемы конструкций на рис. 6.2 | ||||||||||||
| Масса m 1, кг | 3,2 · 103 | 2,0 · 103 | 2,0 · 103 | 3,2 · 103 | 3,7 · 103 | 1,8 · 103 | 2,0 · 103 | 2,0 · 103 | 2,0 · 10 | 2,0 · 10 | 3,0 · 103 | 3,0 · 103 | |
| Масса m 2, кг | 1,6 · 103 | 1,6 · 103 | 1,6 · 103 | 1,6 · 103 | — | 1,9 · 103 | 1,6 · 103 | 1,6 · 103 | 1,6 · 10 | 1,6 · 10 | — | — | |
| Масса m 3, кг | — | — | — | — | — | — | — | — | — | — | |||
| Момент инерции J 1, кг × м2 | 1,5 · 102 | 4,7 · 103 | 4,7 · 103 | 1,5 · 102 | 1,03 · 14 | 4,0 · 102 | — | 4,9 · 103 | 4,7 · 10 | 4,7 · 10 | — | — | |
| Момент инерции J 2, кг × м2 | 4,9 · 103 | 4,9 · 103 | 4,9 · 103 | 4,9 · 103 | — | 5,1 · 103 | — | — | 4,9 · 103 | 4,9 · 103 | 1,5 · 104 | 1,5 · 104 | |
| Координата x 1 O , м | 0,25 | 3,3 | 0,25 | 3,8 | 3,2 | 0,8 | –0,1 | –0,1 | — | — | |||
| Координата y 1 O , м | –0,18 | 0,6 | –0,18 | 0,06 | 0,5 | — | — | 0,1 | 0,1 | — | — | ||
| Координата x 2 O , м | 0,8 | 4,0 | 0,8 | 0,7 | — | * | * | — | — | ||||
| Координата y 2 O , м | 0,06 | 1,0 | 0,5 | 0,06 | 0,8 | 0,02 | — | 0,06 | 0,62 | 0,02 | — | — | |
| Коэффициент трения скольжения f | 0,12 | 0,12 | 0,12 | 0,12 | — | — | 0,12 | — | 0,12 | — | — | — | |
| Жесткость С j, Н · м/рад | 2 · 106 | — | — | 2 · 106 | 2 · 106 | 2 · 106 | — | 2 · 106 | — | 2 · 106 | — | — | |
| Жесткость С Θ, Н · м/рад | — | — | — | — | — | 2 · 106 | 2 · 106 | 2 · 106 | — | — | — | — | |
Продолжение табл. 6.1
| Физическая величина | Номер варианта схемы конструкций на рис. 6.2 | ||||||||||||
| Длина l 1, м | — | 3,8 | 0,6 | 0,6 | 3,8 | 3,8 | — | — | 2,0 | 2,0 | — | — | |
| Длина l 2, м | — | 3,3 | 3,3 | — | — | — | — | — | — | — | — | ||
| Жесткость С 1, Н/м | — | 2 · 106 | 2 · 106 | 2 · 106 | 2 · 106 | 2 · 106 | 6,3 · 105 | — | 2 · 106 | 2 · 106 | — | 3 · 105 … 5 · 105 | |
| Жесткость С 2, Н/м | — | — | 2 · 107 | 2 · 107 | 2 · 107 | — | — | — | 6,3 · 105 | — | — | — | |
| Угол j0, рад | 0; 0,52; 0,78; 1,05 | 0,1; 0,52 | 0; 0,52 | 0; 0,52 | 0; 0,52; 0,78; 1,05 | — | 0; 0,52; 0,78; 1,05 | — | 0; 0,52; 0,78; 1,05 | 0,03... 0,05 | |||
| Угол q0, рад | — | — | — | — | — | 0,1; 0,52 | — | — | — | — | |||
| Координата x 3 0 , м | — | — | — | — | — | 3,3 | — | — | — | — | — | ||
| Радиус R, м | — | — | — | — | — | — | 0,5 | 0,5 | — | — | 1,0 | 0,98 | |
| Координата y 3 0 , м | — | — | — | — | — | 1,0 | — | — | — | 0,6 | — | — | |
| Сила N, Н | — | — | — | — | — | — | — | — | — | — | (4... 6)103 | — | |
| Скорость A 1, м/с | — | — | — | — | — | — | — | — | — | — | 0,02... 0,04 | — | |
| Радиус R 1, м | — | — | — | — | — | — | — | — | — | — | — | 1,0 | |
| Коэффициент трения качения f к, м | — | — | — | — | — | — | 2,0 · 104 | — | — | — | — | — | |
Окончание табл. 6.1
| Физическая величина | Номер варианта схемы конструкций на рис. 6.2 | |||||||||||
| Скорость A2, м/с | — | — | — | — | — | — | — | — | — | — | 0,02... 0,04 | — |
| Частота k 1, 1/с | — | — | — | — | — | — | — | — | — | — | 400... 600 | — |
| Частота k 2, 1/с | — | — | — | — | — | — | — | — | — | — | 500... 700 | — |
| Коэффициент A | — | — | — | — | — | — | — | — | — | — | 0,1... 0,3 | 0,1... 0,3 |
| Коэффициент C | — | — | — | — | — | — | — | — | — | — | 0,3... 0,7 | 0,3... 0,7 |
| Коэффициент D | — | — | — | — | — | — | — | — | — | — | 0,05... 0,1 | 0,05... 0,1 |
| Жесткость С 3, Н/м3 | — | — | — | — | — | — | — | — | — | — | — | (3...5) 108 |
Удлинение  0, м
| — | — | — | — | — | — | — | — | — | — | — | – 0,01 |
Примечание. Символом * отмечены величины, рассчитываемые в процессе решения задачи.
| Т а б л и ц а 6. 2 | |||||||||||||
| Рекомендуемые значения начальных условий обобщенных координат и обобщенных скоростей | |||||||||||||
| Величина | Номер варианта схемы конструкций на рис. 6.2 | ||||||||||||
| q 1(0) | рад | 0; 0,520,78; 1,05 | 0; 0,52 0,78; 1,05 | ||||||||||
| м | |||||||||||||
| q 2(0) | рад | 0; 0,520,78; 1,05 | 0,1; 0,52 | 0; 0,52 | 0; 0,52 | 0; 0,52 | 0,1; 0,52 | 0; 0,520,78; 1,05 | 0,03–0,05 | ||||
| м | |||||||||||||
| q. 1(0) | 1/с | ||||||||||||
| м/с | |||||||||||||
| q. 2(0) | 1/с | ||||||||||||
| м/с |
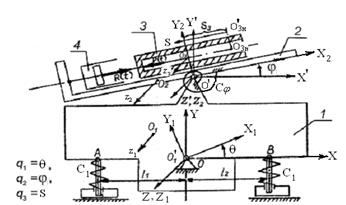
Вариант 1. Полый цилиндр 2 массой m 2 скользит по основанию 1 массой m 1, способному вращаться вокруг неподвижного цилиндрического шарнира О. Основание удерживается спиральной пружиной с крутильной жесткостью 
. В начальном положении механизм находится в состоянии статического равновесия и пружина деформирована. Введем неподвижную систему координат OXYZ так, чтобы ось OX была горизонтальна, и связанную с основанием систему координат OX 1 Y 1 Z 1, ее ось OX 1 параллельна оси цилиндра и направляющим основания, по которым скользит цилиндр. Центр масс основания O 1 в системе координат OX 1 Y 1 Z 1 имеет координаты x 1 О и y 1 O . Начальное положение O н центра масс цилиндра O 2 определяется координатами x 2 O и y 2 O точки O н в системе координат OX 1 Y 1 Z 1.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается нагрузка
(6.1)
где постоянные P 1 = 2, 37×106 H; a 1= 6,68×1010H / c2 ; t 1 = 0,005 c; P 2 = 0 H; a 2= 0 H / c2; t 2= 0 c.
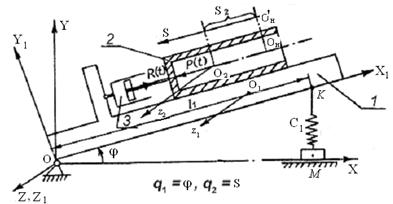
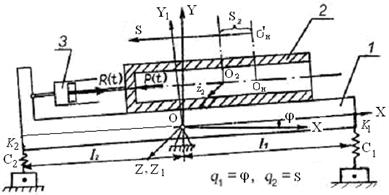
Рис. 6.2
Рис. 6.2. Продолжение
|
Рис. 6.2. Продолжение
|
|
При этом цилиндр 2 начинает двигаться по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией тормозного устройства 3, приложенной к внешней поверхности дна цилиндра:
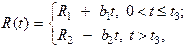(6.2)
где постоянные R 1 = 2,4×105 H; b 1= 5,8×106H/c; t 3= 0,01c;
R 2 = 0 H; b 2= 0 H/c.
Коэффициент трения скольжения при движении цилиндра по основанию f = 0,12. Моменты инерции основания 1 и цилиндра 2 относительно осей O 1 z 1 и O 2 Z 2 равны J 1 и J 2 соответственно. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать угол поворота j основания 1, отсчитанный от горизонтали (в начальный момент j = j0), и координату S центра масс цилиндра 2 на направляющей основания 1, отсчитанную от его начального положения.
Вариант 2. Полый цилиндр 2 массой m 2 скользит по основанию 1 массой m 1, опирающемуся на цилиндрический шарнир О и поддерживаемому вертикальной пружиной КМ. Жесткость пружины C 1, длина недеформированной пружины l 2, расстояние от шарнира О до точки К опоры пружины l 1. Коэффициент трения цилиндра об основание f = 0,12. В начальный момент пружина КМ поддерживает систему в положении статического равновесия.
Введем неподвижную систему координат OXYZ, ось OX которой горизонтальна, и связанную с основанием систему координат OX 1 Y 1 Z 1, ее ось OX 1 параллельна направляющей основания, по которой скользит цилиндр. Положение центра масс O 1 основания задается координатами x 1 O и y 1 O точки O 1 в системе координат OX 1 Y 1 Z 1, причем y 1 O = 0,6 м. Начальное положение цилиндра на основании определяется начальными значениями координат x 2 O и y 2 O точки O 2 в системе координат OX 1 Y 1 Z 1. Точка O н совпадает с начальным положением центра масс цилиндра O 2.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P (t), определяемая по формуле (6.1). При этом цилиндр 2 начинает скользить по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией R (t) тормозного устройства 3, приложенной к внешней поверхности дна цилиндра. Величина реакции определяется по формуле (6.2). Моменты инерции основания 1 и цилиндра 2 относительно осей O 1 z 1 и O 2 z 2 равны J 1 и J 2 соответственно.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать угол поворота j основания 1, отсчитанный от горизонтали, и координату S центра масс цилиндра на направляющей основания, отсчитанную от его начального положения O н. Начальное значение j = j0. Длину недеформированной пружины l 2 определить из условия статического равновесия системы в начальный момент времени.
Вариант 3. Полый цилиндр 2 массой m 2 скользит по основанию 1 массой m 1, опирающемуся на цилиндрический шарнир О, помещенный в центр масс основания. Основание поддерживается двумя вертикальными пружинами с жесткостями C 1 и C 2, отстоящими от оси шарнира на расстояния l 1 и l 2. Коэффициент трения цилиндра о направляющие основания 1 f = 0,12. При начальном положении основания 1 пружины не деформированы. Точки К 1 и К 2 крепления пружин к основанию лежат на оси OX 1. В точке О построены неподвижная система координат OXYZ и система координат OX 1 Y 1 Z 1, неизменно связанная с основанием, так, что ось OX 1 параллельна направляющим основания, по которым скользит цилиндр, и оси цилиндра. Начальное положение цилиндра задается координатами x 2 O и y 2 O центра масс цилиндра O 2 в системе координат OX 1 Y 1 Z 1.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается нагрузка P (t), определяемая по формуле (6.1). При этом цилиндр 2 начинает перемещаться по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией R (t) тормозного устройства 3, определяемой по зависимости (6.2). Моменты инерции основания и цилиндра относительно осей O 1 z 1 и O 2 z 2 равны J 1 и J 2 соответственно.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать угол поворота j основания, отсчитанный от горизонтали, и координату S центра масс цилиндра на направляющей основания, отсчитанную от его начального положения O н. Начальное значение j = j0 = 0.
Вариант 4. Полый цилиндр 2 массой m 2 скользит по основанию 1 массой m 1, опирающемуся на цилиндрический шарнир О, помещенный в центр масс основания. Основание поддерживается двумя вертикальными пружинами с жесткостями C 1 и C 2 и точками крепления K 1 и K 2,отстоящими от оси шарнира О на расстояния l 1 и l 2 соответственно, и спиральной пружиной с жесткостью C j, препятствующей вращению вокруг оси OZ. Введем неподвижную систему координат OXYZ, ось OX которой горизонтальна, и систему координат OX 1 Y 1 Z 1, неизменно связанную с основанием. При этом ось OX 1 параллельна направляющей основания, по которой скользит цилиндр, и оси цилиндра. Точки К 1 и К 2 крепления пружин к основанию лежат на оси OX 1. Положение центра масс O 1 основания задается координатами x 1 O и y 1 O в системе координат OX 1 Y 1 Z 1, причем x 1 O = 0,25 м, y 1 O = –0,18 м. Начальное положение цилиндра на основании определяется начальными значениями координат x 2 O и y 2 O точки O 2 в системе координат OX 1 Y 1 Z 1, причем x 2 O = 0,8 м, y 2 O = 0,06 м. Коэффициент трения при скольжении цилиндра по основанию f = 0,12. Начальный угол наклона основания к горизонту j0 = 0, 30, 45°.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается нагрузка P (t), определяемая по формуле (6.1). При этом цилиндр 2 начинает скользить по основанию 1, вызывая вращение основания вокруг оси OZ. Движение цилиндра тормозится реакцией R (t) тормозного устройства 3, приложенной к внешней поверхности дна цилиндра. Величина реакции определяется по формуле (6.2). Моменты инерции основания и цилиндра относительно осей O 1 z 1 и O 2 z 2 равны J 1 и J 2 соответственно. В начальном положении системы пружины K 1 M 1, K 2 M 2 не деформированы, а спиральная пружина поддерживает систему в состоянии статического равновесия. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать угол поворота j основания, отсчитанный от горизонтали, и координату S центра масс цилиндра на направляющей основания, отсчитанную от его начального положения O н.
Вариант 5. Твердое тело массой m 1 закреплено в цилиндрическом шарнире C, который совершает горизонтальное перемещение, и опирается на вертикальную пружину KM. Координаты центра масс тела O 1 в системе координат OX 1 Y 1 Z 1, неизменно связанной с телом, равны x 1 O и y 1 O . Расстояние от точки С до точки K крепления пружины равно l 1. Жесткость пружины KM равна C 1. К шарниру прикреплена горизонтальная пружина CD жесткостью C 2. Вращение тела относительно оси CZ 1 удерживается спиральной пружиной жесткостью C j, которая в начальном положении не деформирована.
В начальный момент времени к твердому телу параллельно оси CX 1 прикладывается нагрузка P (t), определяемая по формуле (6.1). Линия действия силы P удалена от оси CX 1 на расстояние H = y 2 O . Начальное положение тела задается углом j0 между осью CX 1 и горизонталью. В начальном положении пружина CD не деформирована и тело находится в положении статического равновесия. Момент инерции тела относительно оси O 1 z 1 равен J 1.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать координату xc точки C, отсчитанную от положения статического равновесия пружины CD, и угол поворота j оси CX 1, отсчитанный от горизонтали.
Вариант 6. Полый цилиндр 2 массой m 2 может вращаться вокруг оси O 3 Z 3 шарнира, закрепленного на основании 1 массой m 1. Основание закреплено в цилиндрическом шарнире O и опирается на вертикальную пружину KN с жесткостью С 1. Вращение цилиндра относительно основания сдерживается спиральной пружиной с крутильной жесткостью С j, а вращение основания относительно фундамента – спиральной пружиной с крутильной жесткостью С q. В шарнирах O и O 3 построены системы координат OXYZ и O 3 X 3 Y 3 Z 3, оси OX и O 3 X 3 которых горизонтальны, неизменно связаны с цилиндром и основанием. Расстояние от точки O 3 до оси цилиндра h = 0,06 м. Размеры системы задаются, во-первых, координатами x 3 O = 3,3 м, y 3 O = 1,0 м точки O 3 в системе координат OX 1 Y 1 Z 1, во-вторых, координатами x 2 O = 0,7 м, y 2 O = 0,06 м центра масс цилиндра O 2 в системе координат O 3 X 2 Y 2 Z 2, в-третьих, координатами x 1 O = 3,2 м, y 1 O = 0,5 м центра масс основания 1 в системе координат OX 1 Y 1 Z 1. Длина основания OK равна l 1. Начальное положение системы задается углом q0 между осью OX 1 и горизонталью и углом j0 между осью O 3 X 2 и горизонталью. Моменты инерции основания и цилиндра относительно осей O 1 z 1 и O 2 z 2 равны J 1 и J 2 соответственно. Спиральная пружина в шарнире O в начальном положении не деформирована. При этом пружина в шарнире O3 и вертикальная пружина KN поддерживают систему в положении равновесия.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P (t), определяемая по формуле (6.1). При этом цилиндр начинает вращаться вокруг оси O 3 Z 3, а основание – вокруг оси OZ 1.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать уголq между осью OX 1 и горизонталью и угол j между осью O 3 X 2 и горизонталью O 3 X 3. Момент, возникающий при деформации спиральной пружины в шарнире O 3, вычисляется по формуле
, (6.3)
где b = j – q. Угол bн определяется из условия равновесия цилиндра в начальном положении.
Вариант 7. Полый цилиндр 2 массой m 2 скользит по горизонтальным направляющим, установленным на подвижном основании 1 массой m 1. Основание закреплено на осях колес 3. Масса каждого из четырех колес m 3, радиус колес R. Колеса представляют собой однородные диски. Движение цилиндра по основанию сдерживается пружиной жесткостью C 1. Колеса катятся без скольжения по горизонтальным рельсам. На колеса основания действует момент сопротивления, пропорциональный их угловой скорости: M 3 = –bw3. Вращение колес сдерживается спиральными пружинами с крутильной жесткостью C q. Коэффициент трения при скольжении цилиндра по основанию равен f. Начальное положение цилиндра на основании задается координатой центра масс O 2 цилиндра x 22 = x 2 O в системе координат OX 1 Y 1 Z 1, неизменно связанной с основанием и имеющей оси, параллельные осям неподвижной системы координат OXYZ. Пружины в начальном положении не деформированы.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P (t), определяемая по формуле (6.1). Записать дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать координату центра масс основания O 1 на оси OX и координату x 22 центра масс цилиндра O 2 на оси O 1 X 1. Можно полагать, что в начальный момент x 1 = x 1 O = 0.
Вариант 8. Полый цилиндр 2 массой m 2 вращается вокруг неподвижной оси O 3 Z 2 шарнира, закрепленного на основании 1 массой m 1. Основание установлено на осях колес 3. Масса каждого из четырех колес m 3, радиус колес R. Вращение цилиндра вокруг оси сдерживается спиральной пружиной с крутильной жесткостью C j, а вращение колес – спиральными пружинами с крутильной жесткостью C q. Колеса представляют собой однородные диски, катящиеся по прямолинейному рельсу без проскальзывания. В шарнире O 3 введены промежуточная система координат O 3 X 1 Y 1 Z 1, оси которой параллельны осям OXYZ неподвижной системы координат, и связанная с цилиндром система координат O 3 X 2 Y 2 Z 2, ее ось O 3 X 2 параллельна оси цилиндра. Центр масс цилиндра O 2 лежит на его оси и имеет координаты x 1 O и y 1 O в системе координат O1X2Y2Z2. Момент инерции цилиндра относительно оси O 2 z 2 равен J 2. В начальном положении ось цилиндра составляет угол j0 относительно горизонтали и цилиндр находится в состоянии статического равновесия.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P (t), определяемая по формуле (6.1). Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и е. В качестве обобщенных координат выбрать координату x 1 точки O 3, отсчитываемую от ее начального положения, и угол поворота jоси цилиндра, отсчитанный от горизонтали.
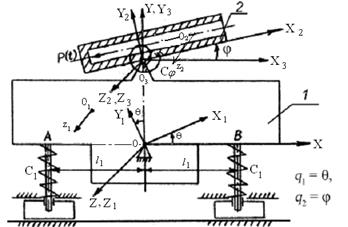
Вариант 9. Полый цилиндр 2 массой m 2 скользит по направляющим основания 1, закрепленного в цилиндрическом шарнире O. Масса основания m 1. Основание в точках A и B опирается на вертикальные пружинные опоры жесткостью C 1. Точки A и B удалены от опоры О на расстояние l 1. Скольжение цилиндра по основанию сдерживается пружиной CD жесткостью C 2. В точке О введены неподвижная система координат OXYZ, ось OX которой горизонтальна, и связанная с основанием система координат OX 1 Y 1 Z 1. В начальный момент система координат OX 1 Y 1 Z 1 совпадает с OXYZ, причем OX 1 проходит через точки A и B. Моменты инерции основания и цилиндра относительно осей O 1 z 1 и O 2 z 2, проходящие через центры их масс, равны J 1 и J 2 соответственно. Центр масс основания O 1 имеет координаты x 1 O и y 1 O в системе координат OX 1 Y 1 Z 1. Ось цилиндра O 2 X 2 удалена на расстояние y 2 O от оси OX 1. Начальное положение цилиндра на направляющих основания определяется из условий статического равновесия системы в начальном положении. При этом пружины не деформированы. Коэффициент трения при скольжении цилиндра по основанию f = 0,12.
В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P (t) (6.1). Это вызывает скольжение цилиндра по основанию и вращение основания вокруг оси OZ. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать угол q отклонения оси OY 1 от вертикали и координату x 2 О центра масс цилиндра O 2 на направляющей основания OX 1.
Вариант 10. Полый цилиндр 2 массой m 2 способен вращаться вокруг оси шарнира O 3, неподвижно закрепленного на основании 1, опирающемся на цилиндрический шарнир O. Масса основания m 1. Основание в точках A и B опирается на вертикальные пружинные опоры жесткостью C 1. Точки A и B удалены от опоры О на расстояние l 1. Вращение цилиндра относительно основания сдерживается спиральной пружиной с крутильной жесткостью C j. В точке О введены неподвижная система координат OXYZ, ось OX которой горизонтальна, и связанная с основанием система координат OX 1 Y 1 Z 1, ее оси в начальном положении совпадают с осями OXYZ, причем ось OX 1 проходит через точки A и B. Центр масс основания O 1 имеет координаты x 1 O = – 0,1 м и y 1 O в системе координат OX 1 Y 1 Z 1. В точке O 3 введены неподвижная система координат O 3 X 3 Y 3 Z 3, оси которой параллельны осям OXYZ, и связанная с цилиндром система координат O 3 X 2 Y 2 Z 2, ее ось O 3 X 2 параллельна оси цилиндра. Центр масс цилиндра O 2 имеет координаты x 2 O и y 1 O в системе координат O 3 X 2 Y 2 Z 2, причем координата y 2 O задана, а координата x 2 O определяется из условий статического равновесия системы в начальном положении. Предполагается, что в начальном положении ось OX 1 горизонтальна, ось O 3 X 2 составляет угол j0 с горизонтом, а пружины в опорах A, B не деформированы.
В начальный момент система координат OX 1 Y 1 Z 1 совпадает с OXYZ. Моменты инерции основания и цилиндра относительно осей O 1 z 1 и O 2 z 2 равны J 1 и J 2 соответственно.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать угол q отклонения оси OY 1 от вертикали и угол jотклонения оси O 3 X 2 от горизонтали. Момент, развиваемый спиральной пружиной, определяется по формуле (6.3).
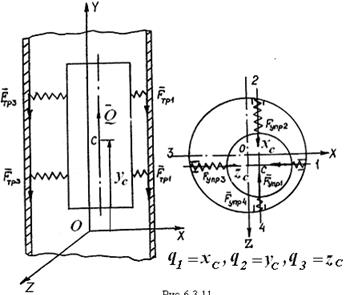
Вариант 11. Цилиндрическое твердое тело массой m 1 движется внутри неподвижной цилиндрической трубы под действием выталкивающей силы Q (t) так, что ось тела совпадает с осью трубы. При этом тело вращается вокруг своей оси симметрии. На теле закреплены два пояса одинаковых упругих амортизаторов по n = 40 амортизаторов в каждом. Опорные поверхности амортизаторов, имеющие форму прямоугольника, в процессе движения тела скользят по поверхности трубы. При этом на амортизатор действует сила трения, направленная в сторону, противоположную скорости центра симметрии А опорной поверхности. Коэффициент трения скольжения зависит от скорости центра симметрии опорной поверхности амортизатора относительно трубы и определяется по формуле
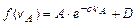, (6.4)
где A, C, D – заданные постоянные, 
– скорость точки A. Сила нормального давления амортизатора на поверхность трубы постоянна и равна N. Амортизаторы установлены и движутся так, что ось симметрии опорной поверхности O 1x составляет одинаковый для них всех и не меняющийся при движении угол a = 0,03 с образующей цилиндрической поверхности трубы. В процессе движения центр симметрии A опорной поверхности совершает малые гармонические колебания в плоскости опорной поверхности так, что производные координаты точки A в системе координат O 1 xz задаются зависимостями
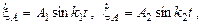
где A 1, A 2, k 1, k 2– заданные постоянные. Точка O 1 представляет собой начальное положение центра симметрии опорной поверхности.
В процессе движения положение точки O 1 в системе отсчета, связанной с движущимся телом, не изменяется. Радиус трубы R = 1 м. Выталкивающая сила Q (t)определяется по формуле
Q (t) = B 1 t2 + B 2 t + B 3, (6.5)
где значение постоянных B 1 = -1,5×106 H/c 2; B 2 = 6,0×106H/c;
B 3 = 1,0×106H. Момент инерции относительно оси CY равен J 1.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и е. В качестве обобщенных координат выбрать координату yС центра масс тела на вертикальной оси, отсчитанную от начального положения центра масс, и угол поворота j тела относительно оси симметрии, отсчитанный от начального положения тела.
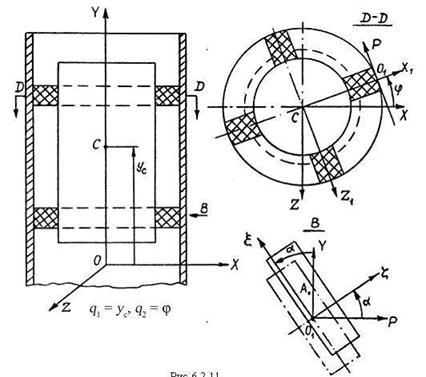
Вариант 12. Цилиндрическое твердое тело массой m 1 движется внутри неподвижной цилиндрической трубы под действием выталкивающей силы Q (t) так, что ось тела совпадает с осью трубы. На теле закреплены два пояса одинаковых упругих амортизаторов по четыре амортизатора в каждом. Их масса пренебрежимо мала. Амортизаторы способны не деформироваться при движении тела в плоскости, перпендикулярной оси трубы. При этом к направляющим трубы в точке М со стороны опорной поверхности амортизатора и к поверхности тела в точке К его крепления прикладывается сила реакции, нелинейно зависящая от удлинения амортизатора,
,
где C 1, C 3 – коэффициенты жесткости амортизатора. Направляющие опорных поверхностей амортизаторов препятствуют перемещению этих поверхностей во всех направлениях, кроме направления, параллельного оси OY. Деформацией амортизаторов в плоскости осевого сечения трубы можно пренебречь. Это позволяет считать, что силы трения, приложенные к опорным реакциям поверхностей амортизаторов со стороны поверхностей направляющих, коаксиальных оси трубы, равны составляющим реакций амортизаторов, приложенным к телу в точках крепления К в направлении, параллельном оси OY. Коэффициент трения скольжения зависит от скорости движения опорной поверхности амортизатора и определяется по формуле (6.4). Начальное положение тела задается величиной угла поворота j. Удлинение амортизаторов в случае, когда точки М и К лежат на одном диаметре, равно 0. Выталкивающая сила Q определяется по зависимости (6.5). Момент инерции тела относительно оси OY равен J 1, радиус трубы R 1 = 1 м, а радиус тела R.
Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Указание. В качестве обобщенных координат выбрать координату yС центра масс тела на оси OY и угол j поворота тела вокруг оси OY.
Схемы конструкций и исходные данные
к вариантам курсовой работы повышенной трудности
Предлагаются варианты задач по расчету динамики механических систем с тремя и более степенями свободы. Задачи предназначены для проведения учебной научно-исследовательской работы. Программирование расчета динамики систем проводится студентами самостоятельно под руководством преподавателя.
 |
 |
 |
Рис. 6.3
 |
 |
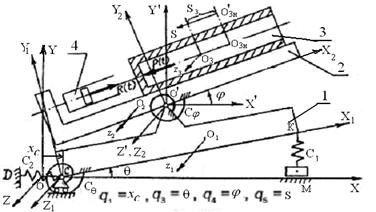Рис. 6.3. Продолжение
 |
 |
 |
Рис. 6.3. Продолжение
 |
|
| Т а б л и ц а 6.3 Значения физических величин для схем конструкций курсовой работы рис. 6.3 | |||||||||||
| Физическая величина | Номер варианта схем конструкций систем | ||||||||||
| Масса m 1, кг | 3,7 · 103 | 2,0 · 103 | 2,0 · 103 | 1,8 · 103 | 2,0 · 103 | 2,0 · 103 | 2,0 · 103 | 2,0 · 103 | 2,0 · 103 | 2,0 · 103 | 3,0 · 104 |
| Масса m 2, кг | — | 1,6 · 103 | 1,6 · 103 | 1,9 · 103 | 3,2 · 103 | 3,2 · 103 | 3,2 · 103 | 3,2 · 102 | 3,2 · 102 | 3,2 · 102 | — |
| Масса m 3, кг | — | — | — | — | 1,6 · 103 | 1,6 · 103 | 1,6 · 103 | 1,6 · 103 | 1,6 · 103 | 1,6 · 103 | — |
| Масса m 4, кг | — | — | — | — | — | — | — | — | — | — | |
| Момент инерции J 1, кг × м2 | 1,03 · 104 | 4,7 · 103 | 4,7 · 103 | 4 · 103 | 4,7 · 103 | 4,7 · 103 | 4,7 · 103 | 4,7 · 103 | 4,7 · 103 | 1,5 · 102 | 1,5 · 102 |
| Момент инерции J 2, кг × м2 | — | 4,9 · 103 | 4,9 · 103 | 5,1 · 103 | 1,5 · 102 | 1,5 · 102 | 1,5 · 102 | 1,5 · 102 | 1,5 · 102 | 4,9 · 103 | — |
| Момент инерции J 3, кг × м2 | — | — | — | — | 4,9 · 103 | 4,9 · 103 | 4,9 · 103 | 4,9 · 103 | 4,9 · 103 | — | — |
| Радиус R, м | — | — | — | — | — | — | — | — | — | 0,5 | 0,98 |
| Координата x ¢1 O , м | — | — | — | — | 3,3 | 3,3 | 3,3 | 0,25 | — | ||
| Координата y ¢1 O , м | — | — | — | — | 0,5 | 0,5 | 0,5 | 0,55 | — | — | |
| Координата x 1 O , м | — | 3,3 | 3,3 | 3,2 | — | — | — | — | — | — | — |
| Координата y 1 O , м | 1,0 | 0,6 | 0,6 | 0,5 | — | — | — | — | — | — | — |
| Координата x ¢2 O , м | — | — | — | 0,7 | 0,25 | 0,25 | 0,25 | 0,25 | 0,25 | 0,8 | — |
| Координата y ¢2 O , м | — | — | — | 0,02 | –0,18 | –0,18 | –0,18 | –0,18 | –0,18 | 0,06 | — |
| Координата x 2 O , м | 3,8 | 4,0 | 4,0 | 4,0 | — | — | — | — | — | — | — |
| Координата y 2 O , м | 0,8 | 1,0 | 1,0 | 1,0 | — | — | — | — | — | — | — |
| Координата x 0¢ О, м | — | — | — | — | 3,3 | 3,3 | 3,3 | –0,05 | — | — | |
| Координата y 0¢ O, м | — | — | — | — | 1,0 | 1,0 | 1,0 | 0,4 | 0,95 | 1,0 | — |
| Координата x 3 О , м | — | — | — | — | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | — | — |
| Окончание табл. 6. 3 | |||||||||||
| Физическая величина | Номер варианта схем конструкций систем рис.6.3 | ||||||||||
| Координата y3О, м | — | — | — | — | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | — | — |
| Длина l 1, м | 3,8 | 3,8 | 3,8 | 3,8 | 3,8 | 3,8 | 3,8 | 0,6 | 2,0 | — | — |
| Длина l 2, м | — | — | — | — | — | — | — | 3,3 | — | — | — |
| Начальное удлинение l0, м | — | — | — | — | — | — | — | — | — | — | –0,01 |
| Жесткость С 1, Н/м | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | — | — |
| Жесткость С 2, Н/м | 2,0 · 107 | 2,0 · 107 | 2,0 · 107 | 2,0 · 107 | — | 2,0 · 107 | 2,0 · 107 | 2,0 · 107 | — | — | — |
| Жесткость С 3, Н/м | 2,0 · 107 | — | 2,0 · 107 | — | — | — | 2,0 · 107 | — | — | — | — |
| Крутильная жесткость С j, Н · м/рад | 2,0 · 106 | 2,0 · 106 | — | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | — |
| Крутильная жесткость С q, Н · м/рад | — | — | — | 2,0 · 106 | 2,0 · 106 | 2,0 · 106 | — | — | — | 2,0 · 106 | — |
| Коэффициент трения скольжения f | — | 0,12 | 0,12 | — | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | 0,12 | — |
| Угол j0, рад | 6˚, 30˚ | 6˚, 30˚ | 6˚, 30˚ | 0˚, 30˚, 45˚ 60˚ | 0˚, 3 0˚, 45˚ 60˚ | 0˚, 30˚, 45˚ 60˚ | 0˚, 30˚, 45˚ 60˚ | 0˚, 30˚, 45˚ 60˚ | 0˚, 30˚, 45˚ 60˚ | 0˚, 30˚, 45˚ 60˚ | 1˚, 3˚ |
| Угол q0, рад | — | — | — | 6˚, 30˚ | 6˚, 30˚ | 6˚, 30˚ | 6˚, 30˚ | — | — | — | — |
| Жесткость С 4, Н/м | — | — | — | — | — | — | — | — | — | — | 3,0 · 108 ... 5,0 · 108 |
| Коэффициенты A, C, D | — | — | — | — | — | — | — | — | — | — | см. табл. 6.1 |
Вариант 1. Взяв за основу механическую систему варианта 5 (рис. 6.2) курсовой работы, полагаем дополнительно, что к шарниру C прикреплена еще и вертикальная пружина CE жесткостью C 3.
К обобщенным координатам, указанным на рис. 6.2, вар.5, добавить координату yС точки C на вертикальной оси, отсчитанную от положения статического равновесия пружины CE. Рекомендуемые значения постоянных приведены в табл. 6.3.
Вариант 2. Взяв за основу механическую систему варианта 2 (рис. 6.2) курсовой работы, полагаем дополнительно, что к шарниру C прикреплена горизонтальная пружина CD с жесткостью C 2. В начальном положении пружина CD не деформирована и система находится в состоянии статического равновесия.
К обобщенным координатам, указанным на рис.6.2, добавить координату xС точки C на горизонтальной оси, отсчитанную от положения статического равновесия пружины CD.
Вариант 3. Взяв за основу механическую систему варианта 2 (рис. 6.3) курсовой работы, полагаем дополнительно, что к шарниру C прикреплена вертикальная пружина CE жесткостью C 3.
К обобщенным координатам, указанным в вар. 2, добавить координату yС точки C на вертикальной оси, отсчитанную от положения статического равновесия пружины CE. Рекомендуемые значения постоянных приведены в табл. 6.3.
Вариант 4. Взяв за основу механическую систему варианта 6 (рис. 6.2) курсовой работы, полагаем дополнительно, что к шарниру C прикреплена горизонтальная пружина CD жесткостью C 2. В начальном положении пружина CD не деформирована и система находится в состоянии статического равновесия.
К обобщенным координатам, указанным на рис. 6.2, вар. 6, добавить координату xС шарнира C на горизонтальной оси, отсчитанную от положения статического равновесия пружины CD.
Вариант 5. Полый цилиндр 3 массой m 3 скользит по направляющей 2 массой m 2, способной вращаться вокруг цилиндрического шарнира О′, закрепленного на основании 1 массой m 1. Основание закреплено в цилиндрическом шарнире C и опирается на вертикальную пружину KM с жесткостью C 1. Длина недеформированн
