Схемы конструкций представлены на рис. 5.1, исходные данные – в табл.5.1.
Последняя цифра зачетной книжки (шифр) является основанием для выбора варианта задачи. По последней цифре шифра (ПЦШ) выбирается номер схемы и номер условий в соответствующей таблице. Конкретно задача сформулирована в соответствии с номером рисунка схемы.
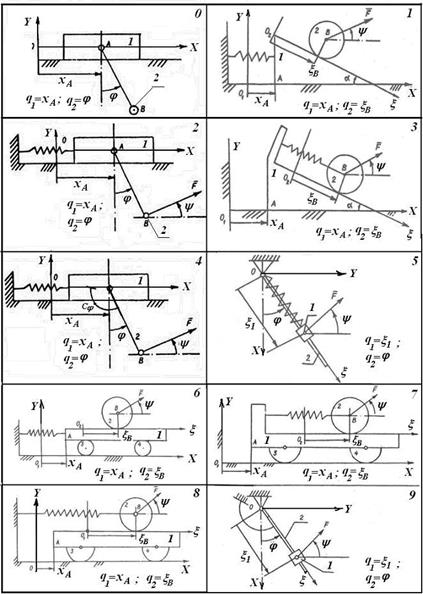
Рис. 5.1. Схемы конструкций к расчетной работе №2
Т а б л и ц а 5.1
| Пара-метры | Схемы конструкцийй - (ПЦШ) | |||||||||
| m 1 , кг | ||||||||||
| m 2 , к | ||||||||||
| m 3 , кг | - | - | - | - | - | - | - | |||
| m 4 , кг | - | - | - | - | - | - | - | - | - | |
| C 1 , Н/м | - | - | - | |||||||
| C φ, Нм/рад | - | - | - | - | - | - | - | - | ||
| l,м | - | - | 0,1 | - | - | - | - | |||
| R, м | - | - | - | - | - | - | - | 0,2 | 0,2 | - |
| l 2,м | - | - | - | - | - | 0,4 | - | - | - | |
| F, H | - | |||||||||
| ω, с-1 | π | π | π | π | π | π | π | π | π | π |
| f к, М | - | - | - | - | - | - | - | 0,1 | 0,1 | |
| α, рад | 0,5 | 0,5 | ||||||||
| q 1(0), м | 0,1 | |||||||||
| q 2(0), рад q 2(0), м | 1,0 | |||||||||
 , м/c
| 0,1 |
Здесь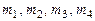 
- массы; 
- линейная жесткость пружины; 
- крутильная жесткость пружины; l, l2 - длины; R - радиус; F - сила; 
- частота, с-1;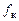 
- коэффициент сопротивления качению; 
- угол, рад;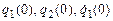 
, все
= 0 с-1, мс-1 - рекомендуемые значения начальных условий обобщенных координат и скоростей.
Вариант 0. Ползун 1 массой m 1 может скользить без трения по горизонтальной направляющей. К ползуну подвешен математический маятник 2 длиной l имассой m 2. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Вариант 1. Призма 1, имеющая массу m 1, скользит по гладкой горизонтальной плоскости, удерживаемая горизонтальной пружиной жесткостью С 1. По наклонной грани призмы катится без скольжения однородный цилиндр 2, имеющий массу m 2. К его центру под углом Y к горизонту приложена сила 
, величина которой постоянна. Угол Y линейно меняется со временем: 
. Угол наклона призмы к горизонту a. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и я. 1. Обобщенная координата 
отсчитывается от положения призмы, при котором пружина не деформирована.
2. При задании величин F, m 2, a следует соблюдать условие 
, кг.
Вариант 2. Ползун 1 прикрепленный к основанию горизонтальной пружиной жесткостью С 1 массой m 1 скользит без трения по горизонтальной направляющей. К ползуну подвешен математический маятник 2 длиной l имассой m 2, к точке B маятникаприложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно меняется со временем: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и е. Обобщенная координата отсчитывается от положения ползуна, при котором пружина не деформирована.
Вариант 3. Призма 1, имеющая массу m 1, скользит по наклонной плоскости без трения. По наклонной грани призмы катится без скольжения однородный цилиндр 2, массой m 2, центр которого прикреплен к призме пружиной жесткостью С 1. К центру диска 2 под углом Y к горизонту приложена сила , величина которой постоянна. Угол Y линейно меняется со временем: . Угол наклона призмы к горизонту a. Пружина параллельна грани призмы. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и я. 1. Обобщенная координата 
отсчитывается от положения центра диска, при котором пружина не деформирована.
2. При задании величин F, m 2, a следует соблюдать условие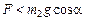 
, кг.
Вариант 4. Ползун 1 массой m 1 скользит без трения по горизонтальной направляющей. К ползуну подвешен математический маятник 2 длиной l имассой m 2, связанный с ползуном спиральной пружиной с крутильной жесткостью С j. При нижнем положении маятника пружина не деформирована. К точке B маятникаприложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно меняется со временем: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Вариант 5. Груз 1 массой m 1 и пренебрежимо малых размеров может скользить без трения по стержню 2 достаточно большой длины l 2имассой m 2, будучи удерживаемым пружиной жесткостью С1. Длина недеформированной пружины l. К грузуприложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно меняется со временем: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Вариант 6. Доска 1 массой m 1может передвигаться на роликах 3, 4 с массой m 3 = m 4 , катящихся без скольжения по горизонтальной плоскости. По доске 1 катится без скольжения цилиндр 2 массой m 2. Доска удерживается горизонтальной пружиной жесткостью С 1. К оси цилиндраприложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно меняется со временем: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и я. 1. Обобщенная координата отсчитывается от положения края доски, при котором пружина не деформирована.
2. При задании величин F, m 2 следует соблюдать условие 
.
Вариант 7. Тележка 1 массой m 1, имеющая два колеса 3, 4 массой m 3 = m 4 , может катиться без сопротивления по горизонтальной плоскости. При этом колеса катятся без скольжения. По тележке 1 катится без скольжения однородный диск 2 массой m 2, центр которого соединен с тележкой горизонтальной пружиной жесткостью С 1. К центру диска 2 приложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно зависит от времени: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и я. 1. Обобщенная координата отсчитывается от положения центра диска 2, при котором пружина не деформирована.
2.При задании величин F, m 2следует соблюдать условие .
Вариант 8. Тележка 1 массой m 1, имеющая два колеса 3, 4 массой m 3 = m 4 , может катиться без сопротивления по горизонтальной плоскости. При этом колеса катятся без скольжения. По тележке 1 катится без скольжения однородный диск 2 массой m 2, центр которого соединен с неподвижным основанием горизонтальной пружиной жесткостью С 1. К центру диска 2 приложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно зависит от времени: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
У к а з а н и я. 1. Обобщенная координата отсчитывается в системе координат, неизменно связанной с тележкой, причем так, что при = 0, = 0, пружина не деформирована.
2. При задании величин F, m 2следует соблюдать условие .
Вариант 9. Груз 1 массой m 1 и пренебрежимо малых размеров может скользить без трения по стержню 2 достаточно большой длины l 2имассой m 2. Стержень удерживается спиральной пружиной с крутильной жесткостью С j. В нижнем положении стержня пружина не деформирована. К грузуприложена постоянная по величине сила , составляющая угол Y с горизонтом. Угол Y линейно меняется со временем: . Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Пример. Дано. Центры однородных дисков (рис. 5.2), способных катиться по горизонтальной плоскости без скольжения, связаны пружиной, коэффициент жесткости которой равен C. Массы дисков m 1 и m 2. К диску 1 приложен момент сил сопротивления качению M 1 Z = – 
ω1 Z, а к диску 2M 2 Z = – 
ω2 Z, пропорциональные соответствующим угловым скоростям. К центру диска 2 приложена постоянная по величине сила , составляющая угол Ψ с горизонтом. Угол Ψ линейно зависит от времени: Ψ = ω t. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
Рис. 5.2
В соответствии с разд. 2 составим дифференциальные уравнения, описывающие движение системы (рис. 5.2).
1. Выберем обобщенные координаты. Для этого введем горизонтальные оси O 1 X 1 и O 2 X 2, неизменно связанные с плоскостью, по которой катятся диски. Начала отсчета O 1 и O 2 на этих осях выберем так, чтобы расстояние O 1 O 2 равнялось длине недеформируемой пружины. В качестве обобщенных координат выберем координату центра A диска 1 на оси OX 1 и координату центра B диска 2 на оси OX 2:
q 1 = x 1 A, q 2 = x 2 B.
2. Представим кинетическую энергию системы в виде
T = T (t, q 1, q 2, 
). Она складывается из кинетических энергий дисков, каждый из которых совершает плоскопараллельное движение. При этом T = T 1 + T 2, где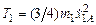 
, 
. В итоге, переходя к обозначениям 
, получаем
. (5.1)
3. Определим обобщенные силы. Для этого рассмотрим систему сил, приложенных к системе материальных точек, состоящую из сил, не зависящих от ограничивающих тел и сил трения. В эту систему войдут сила F–, силы тяжести P– 1 и P– 2, реакции пружины R– 1, R– 2, моменты сил сопротивления M– 1и M– 2. Введем в рассмотрение оси AZ 1 и BZ 2(рис. 5.2). Алгебраические величины указанных сил и моментов на соответствующих осях могут быть записаны в виде
(5.2)
При записи выражений для сил реакций пружины учтем, что из-за выбора обобщенных координат разница между текущей длиной пружины l и длиной недеформированной пружины l 0 равна разности координат центров дисков: l – l 0 = x 2 B + l 0 – x 1 A – l 0 = x 2 B – x 1 A, поэтому
(5.3)
Рассмотрим виртуальное перемещение системы, при котором обобщенная координата q 1 = x 1 A получает приращение δ q 1 = δ x 1 A, а обобщенная координата q 2 = x 2 B не меняется. Сосчитаем виртуальную работу:
δ Aq 1 = R 1 X 1 δ x 1 A + M 1 Z δφ1,
где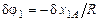 
– приращение угла поворота, соответствующее приращению δ x 1 A координаты центра диска 1, тогда
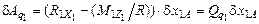. (5.4)
Отсюда с учетом (5.3), (5.4) получим выражение для первой обобщенной силы:
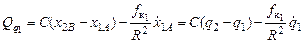. (5.5)
Рассмотрим виртуальное перемещение системы, при котором обобщенная координата q 1 = x 1 A не меняется, а q 2 = x 2 B получает приращение δ q 2 = δ x 2 B. Аналогично (5.3) … (5.5) сосчитаем виртуальную работу и получим выражение для обобщенной силы:
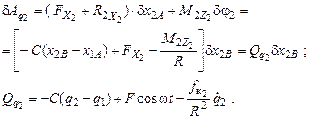
4. Дифференцируя выражение для кинетической энергии (5.1), составим уравнения Лагранжа II рода:
(5.6)
или
Курсовая работа
