а) образование;
б) комплексные чертежи;
в) принадлежность точки поверхности.
1. Конические поверхности задаются движением прямой линии l, проходящей через неподвижную точку М, по некоторой направляющей кривой линии а. (рис 128)
2. Цилиндрические поверхности задаются движением прямой, параллельной некоторому направлению, по заданной направляющей кривой. (рис 129)


Экзаменационный билет №_27
Построение точки пересечения кривой поверхности с прямой линией общего положения
1. Выполнить комплексный чертеж сферы и пересекающей ее прямой общего положения;
2. Определить точки пересечения, видимость прямой и составить алгоритм решения.
3. Ответить на следующие вопросы:
а) к какому типу относится данная задача;
б) по какой схеме решается такого типа задача;
в) какой принцип положен в основу выбора вспомогательной плоскости.
| Словесная форма | Графическая форма |
| Y.Ì1. Заключить данную прямую линию а во вспомогательную плоскость Y, a Вспомогательную плоскость следует выбирать так, чтобы в результате получались простейшие сечения (линии, окружности) | 
|
| 2. Определить линию пересечения l вспомогательной плоскости Y с заданной поверхностью, Y∩a– l(1-2-3-4-5-6) | 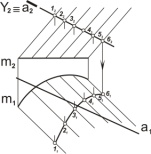
|
| 3. Соединить точки полученной линии пересечения с данной линией а, Y∩a-l(1-2-3-4-5-6). 4. Определить видимость прямой линии а | 
|
Экзаменационный билет №_28
Пересечение кривой поверхности с плоскостью (2-я позиционная задача).
1. Выполнить комплексный чертеж прямого кругового конуса и пересекающего его плоскости общего положения.
2. Определить линию их пересечения и видимость.
3. Ответить на следующие вопросы:
а) какая линия получилась при пересечении;
б) какой способ применялся для построения точек принадлежащих этой линии, его сущность;
в) какие опорные точки имеет линия и как они определялись.
г) какие линии можно получить при пересечении конуса плоскостью.
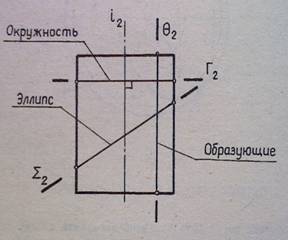
В сечении могут быть получены следующие линии:
1. Окружность, если секущая плоскость Г (Г2)┴ оси i (i2).
2. Эллипс, если секущая плоскость Σ (Σ2) не параллельна и не перпендикулярна оси i (i2).
3. Две образующие, если секущая плоскость θ (θ2) параллельна оси i (i2) (рис.3).
Экзаменационный билет №_29
Комплексные задачи:
1. Выполнить комплексный чертеж прямой общего положения и точки, не лежащей на ней.
2. Определить расстояние от точки до прямой, не пользуясь способом преобразования комплексного чертежа и составить алгоритм решения задачи.
3. Ответить на следующие вопросы:
а) какие задачи называют комплексными;
б) какова схема их решения;
в) в какой последовательности реализуется схема (анализ, исследование, построение).

Экзаменационный билет №_30




