1.Выполнить комплексный чертеж 2-х поверхностей вращения, оси которых пересекаются в одной фронтальной плоскости уровня;
2. Построить линию пересечения, используя в качестве вспомогательных поверхностей концентрические сферы, определить видимость;
3. Ответить на следующие вопросы:
а) на чем основан способ сфер;
б) где располагается центр вспомогательных сфер и почему;
в) как определить R min и R max сфер;
г) как определить точки, принадлежащие линии пересечения;
д) в каких случаях можно использовать способ концентрических сфер.
Прежде чем строить промежуточные точки, необходимо найти опорные точки линии пересечения. Точки А, В, K и L, а также E, F, С и D – это точки, принадлежащие контурам поверхностей. Их можно найти способом концентрических сфер или с помощью плоскостей посредников Σ(Σ2) и Δ(Δ1).
Рассмотрим теперь построение промежуточных точек на примере точек 5 и 6. Построения выполняем на фронтальной плоскости проекций. Сфера посредник Θ(Θ2) с центром в точке О (О 2) пересекает конические поверхности по окружностям, которые на П 2 проецируются в отрезки 
и 
(проекции двух других окружностей не показаны). Точки 52 = 62 их пересечения являются фронтальными проекциями точек 5 и 6, которые принадлежат линии пересечения поверхностей, так как принадлежат каждой из этих поверхностей.
Горизонтальные проекции точек 5 и 6 находим из условия принадлежности точки поверхности. В данном случае используется принадлежность точек окружности mi на «вертикальной» конической поверхности. Точки 52 и 62 находятся по линии проекционной связи на 
.
Аналогично можно построить любое количество точек искомой линии пересечения. Однако нужно иметь в виду, что не все сферы могут быть использованы для решения задачи.
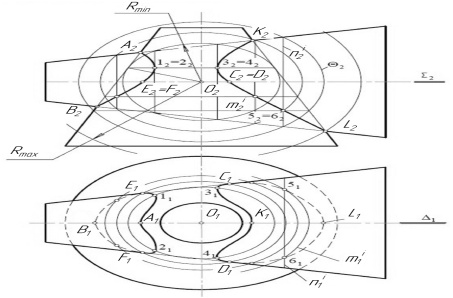
Рассмотрим предельные границы вспомогательных сфер. Радиус сфер посредников изменяется в диапазоне R max ≥ R ≥ R min, где R min – минимальный радиус сферы, R max – максимальный радиус сферы. Сфера минимального радиуса R min – это сфера, которая касается одной поверхности и пересекает другую. На рис. 54 такая сфера касается «вертикальной» конической поверхности. С помощью сферы минимального радиуса построены точки 12 = 22 и 32 = 42. Горизонтальные проекции точек 1, 2, 3 и 4 построены аналогично точкам 5 и 6.
Радиус максимальной сферы равен расстоянию от точки пересечения осей поверхностей до самой удаленной точки пересечения контурных образующих этих поверхностей. На рис 54 – сфера R max =[ O 2 L 2].
Для установления видимости проекций линии пересечения анализируем расположение точек относительно контуров поверхностей. Так, относительно П 1, видимым будет участок кривой, расположенный выше контура горизонтальной конической поверхности (вторая поверхность на видимость на П 1 не влияет). Горизонтальная проекция невидимой части линии показана штриховой линией.
Точки А, В и K, L принадлежат фронтальным контурам поверхностей и отделяют видимую часть линии пересечения от невидимой при проецировании на П 2. Фронтальные проекции видимой и невидимой частей линии пересечения на рис. 54 совпадают.
Экзаменационный билет №_22
