а) цилиндрическая винтовая линия (ее проекции, развертка и свойства)
Проекции кривой линии имеют следующие свойства: В общем случае проекция кривой линии есть кривая линия; Если точка принадлежит кривой линии, то её проекции принадлежат одноименным проекциям кривой; Касательная к кривой линии проецируется в касательную к проекциям кривой линии.
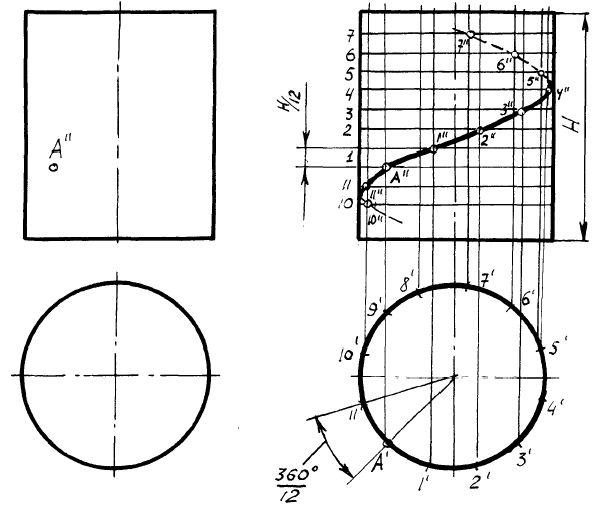
ПРИМЕР 1. Построить проекции правой цилиндрической винтовой линии, проходящей через точку поверхности цилиндра. Рисунок 2 – Пример 1. РЕШЕНИЕ. Находим точку A/. Начиная с точки A/, делим окружность основания цилиндра на 12 частей. Высоту цилиндра H делим на 12 частей, начиная с точки A//. На пересечении вертикальных и горизонтальных одноименных линий находим точки винтовой линии, которые плавно соединяем
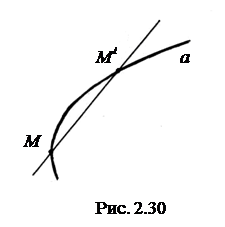
Касательной в данной точке M к кривой a называется предельное положение секущей прямой, проведенной через точку M, когда ее длина становится равной нулю. На рис проведена секущая MM1. Пусть точка M1 двигается вдоль кривой по направлению к точке M. В момент совпадения точек M1 и M секущая становится касательной. Нормалью в данной точке M называется прямая, перпендикулярная к касательной.
Большое значение при рассмотрении плоских алгебраических кривых линий имеет определение порядка кривой. Это определение может быть дано как алгебраически (порядком кривойназывается степень ее алгебраического уравнения), так и геометрически (порядком плоской алгебраической кривой называется число точек пересечения кривой с прямой линией). При этом надо иметь в виду, что в число точек пересечения включаются как точки с действительными, так и с мнимыми координатами.
Из свойств параллельного проецирования вытекают свойства кривых линий, которые сохраняются у их проекций:
- если точка А принадлежит кривой m (рис. 1.47), то проекция А1 этой точки принадлежит проекции m1 кривой;
- секущая n и касательная t к кривой линии проецируются соответственно в секущую n1 и касательную t1 к проекции кривой m1 (рис. 1.47);
- бесконечно удаленные точки кривой линии, например  , проецируются в бесконечно удаленные точки ее проекции
, проецируются в бесконечно удаленные точки ее проекции  ;
;
- порядок плоской алгебраической кривой при параллельном проецировании не меняется, т. е. сохраняется число точек пересечения кривой и прямой линий.

Рассмотрим основные свойства проекций плоских кривых линий.
Порядок плоской алгебраической кривой при параллельном проецировании не изменяется.
Проведём секущую m кривой l, лежащей в плоскости W. Тогда в проекции получим прямую m ¢, а точки пересечения линий m и l спроецируются в точки пересечения проекций m ¢ и l ¢ в соответствии с рисунком 1.3.27.
Таким образом, число точек пересечения линий m и l будет равно числу точек пересечения их проекций m ¢ и l ¢, т.е. порядок проекции l ¢ будет равен порядку кривой l.
Бесконечно удалённые точки кривой проецируются в бесконечно удалённые точки её проекции.
При перемещении некоторой точки М по кривой l её проекция М¢ будет перемещаться по кривой l ¢. При удалении точки М в бесконечность в соответствии с рисунком 1.3.27 её проекция также станет бесконечно удалённой точкой.
Касательная к кривой проецируется в касательную к её проекции.
Точка А¢ есть проекция точки А. Прямая t ¢ является проекцией прямой t, касательной к кривой l в точке А.
Число точек пересечения плоских кривых сохраняется при проецировании.

Цилиндрическая винтовая линия 1) представляет собой пространственную кривую линию одинакового уклона. Острие резца, соприкасаясь с поверхностью равномерно вращающегося цилиндрического стержня, оставляет на нем след в виде окружности. Если же при этом сообщить резцу равномерное поступательное движение вдоль оси цилиндра, то на поверхности цилиндра получится цилиндрическая винтовая линия.
На рис. 301 показано образование винтовой линии на поверхности цилиндра 2) от движения точки А по образующей ЕС и вращательного движения этой образующей. Здесь изображено несколько положений этой образующей: E0С0, E1,С1...;

Если при перемещении образующей из положения Е0С0 в положение Е1С1 точка займет положение А1 то отрезок Е1А1 определит расстояние, которое точка прошла по образующей от своего первоначального положения. При последующем положении образующей (Е2С2) точка поднимется на высоту Е2А2 = 2Е1А1 и т. д. Когда образующая сделает полный оборот, точка переместится по ней на расстояние E0Al2 = 12Е1А1.
При дальнейшем вращении образующей точка А начнет образовывать второй виток, или оборот винтовой линии, занимая положения А11, А12 и т. д.
Расстояние между точками А0 и А12 называется шагом винтовой линии. Шаг может быть выбран в зависимости от тех или иных условий.
Экзаменационный билет №_14






