Выполнить комплексный чертеж плоскости общего положения и пересекающей ее прямой общего положения;
Определить точку их пересечения;
3. Ответить на следующие вопросы:
а) к какому типу относится данная задача;
б) по какой схеме решаются задачи такого типа;
в)по какому алгоритму решалась задача и его отличие от схемы
г) как определялась видимость прямой.
Дано: α(ABC) – плоскость общего положения;
a(a1,a2) – прямая общего положения.
Определить: K=a×α(ABC).
Решение:
1. Прямую заключить во вспомогательную плоскость частного положения: a∈β.
2. Определить линию l как линию пересечения вспомогательной и заданной плоскостей l=α(ABC)∩ β.
3. Определить взаимное положение заданной прямой a и полученной прямой l. Поскольку прямые a и l лежат в одной плоскости, они могут пересекаться или быть параллельными. Точка пересечения K=a×l и является искомой точкой пересечения прямой а с плоскостью α(ABC). Если прямые a и l параллельны, то прямая а параллельна плоскости α(ABC).

Тип задачи – позиционная
Экзаменационный билет №_7
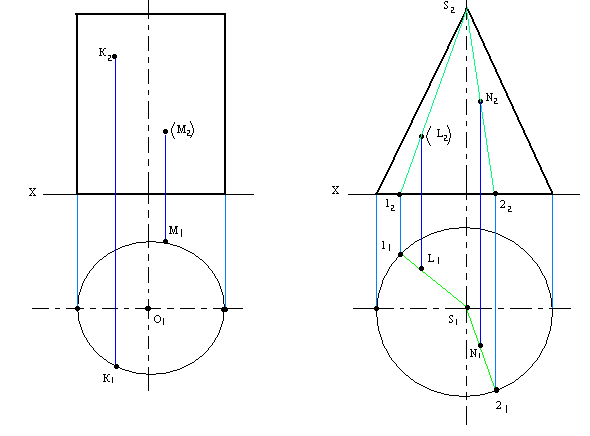
При пересечении многогранника с прямой получаем две точки (точку входа и точку выхода).
Для их нахождения необходимо:
1.Через данную прямую провести проецирующую вспомогательную плоскость Qп2.
2.Находим сечение многогранника вспомогательной проецирующей плоскостью
3.Определяем точки пересечения данной прямой с сечением – это и есть искомые точки.
Часть прямой внутри многогранника невидимая.

Экзаменационный билет №_8
Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима.
1 способ. Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.
2 способ. Точка А лежит на параллели конуса радиусом r. На π1 строим проекцию окружности (параллели) и по линии проекционной связи находим А 1. По двум проекциям точки строим третью.

Экзаменационный билет №_9
 Тип задачи – позиционная
Тип задачи – позиционная
Экзаменационный билет №_10
Взаимно- перпендикулярные прямые и плоскости.
Теоретической предпосылкой для построения на комплексном чертеже проекций прямых и плоскостей, перпендикулярных по отношению друг к другу в пространстве, служит свойство проекции прямого угла, одна из сторон которого параллельна какой-либо плоскости проекции:
Если одна из сторон прямого угла параллельна плоскости проекции, то на данную плоскость прямой угол будет проецироваться прямым углом.



Изобразить на комплексном чертеже:
а) взаимно- перпендикулярные прямая и плоскость (Выполнить комплексный чертеж плоскости общего положения и провести прямую, перпендикулярную к этой плоскости)
б) взаимно- перпендикулярных плоскостей. (Выполнить комплексный чертеж плоскости общего положения и построить препендикулярную к ней плоскость общего положения
Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Из множества этих прямых при построении перпендикуляра к плоскости на чертеже выбирают фронталь и горизонталь плоскости, так как при этом образуются прямые углы, одна из сторон которых параллельна плоскости проекций. В этом случае на чертеже фронтальную проекцию перпендикуляра проводят под углом 90° к фронтальной проекции фронтали, а горизонтальную проекцию перпендикуляра — под углом 90° к горизонтальной проекции горизонтали.
Построение двух взаимно перпендикулярных плоскостей. Как известно, плоскости перпендикулярны, если прямая, принадлежащая одной плоскости, перпендикулярна другой плоскости. Построение проекций плоскости Р, проходящей через прямую с проекциями т'п', тп и перпендикулярной плоскости, заданной проекциями a'b'c', abc треугольника, показано на рисунке 4.21. Для построения на чертеже плоскости через проекции е', е точки прямой проведены проекции e'f, ef перпендикуляра к плоскости треугольника. Две пересекающиеся прямые определяют положение искомой плоскости, перпендикулярной к заданной. Заметим, что построение проекций e'f и ef перпендикуляра к заданной плоскости облегчено тем, что стороны треугольника с проекциями a'b', ab — фронталь, а'с', ас — горизонталь.


Экзаменационный билет №_11






