а ¾ продольная сила N приложена между равнодействующими усилий
в арматуре S и S¢; б ¾ то же, за пределами расстояния между равнодействующими усилий в арматуре S и S¢
Если полученное из расчета по формуле (160) значение х > xRh 0, в условие (159) подставляется х = xRh 0, где xR определяется по табл. 18 и 19.
Если х < 0, прочность сечения проверяется из условия (157).
При симметричном армировании прочность независимо от значения е¢ проверяется из условия (157).
Примечание. Если при e ¢ > h 0 – a ¢ высота сжатой зоны, определенная без учета сжатой арматуры 
, меньше 2 а ¢, расчетную несущую способность можно несколько увеличить, произведя расчет по формулам (159) и (160) без учета сжатой арматуры.
3.79. Требуемое количество продольной арматуры определяется следующим образом:
а) при e ¢ £ h 0 – a ¢ определяется площадь сечения арматуры S и S¢ соответственно по формулам:
(161)
(162)
б) при e ¢ > h 0 – a ¢ определяется площадь сечения растянутой арматуры As по формуле
(163)
где x принимается по табл. 20 в зависимости от значения
(164)
При этом должно удовлетворяться условие am £ aR (см. табл. 18 и 19). В противном случае следует увеличить сечение сжатой арматуры 
, повысить класс бетона или увеличить размеры сечения.
Если am < 0, площадь сечения растянутой арматуры As определяется по формуле (161).
Площадь симметричной арматуры независимо от значения е ¢ подбирается по формуле (161).
Примечание. При е ¢ > h 0 – a ¢ необходимое количество арматуры, определенное по формуле (161), можно несколько снизить, если значение x, определенное по табл. 20 без учета сжатой арматуры, т. е. по значению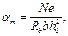 
окажется меньше 2 а ¢/ h 0. В этом случае площадь сечения растянутой арматуры As определяется по формуле
(165)
где z определяется по табл. 20 в зависимости от значения 
ОБЩИЙ СЛУЧАЙ РАСЧЕТА НОРМАЛЬНЫХ СЕЧЕНИЙ
ВНЕЦЕНТРЕННО РАСТЯНУТОГО ЭЛЕМЕНТА
(ПРИ ЛЮБЫХ СЕЧЕНИЯХ, ВНЕШНИХ УСИЛИЯХ
И ЛЮБОМ АРМИРОВАНИИ)
3.80. Расчет сечений внецентренно растянутого элемента в общем случае (см. черт. 45) должен производиться из условия
(166)
где 
¾ расстояние от продольной силы N до оси, параллельной прямой, ограничивающей сжатую зону, и проходящей через точку сжатой зоны, наиболее удаленную от указанной прямой;
Sb ¾ статический момент площади сжатой зоны бетона относительно указанной оси;
Ssi ¾ статический момент площади сечения i -го стержня продольной арматуры относительно указанной оси;
ssi ¾ напряжение в i -м стержне продольной арматуры.
Высота сжатой зоны х и напряжения ssi определяются из совместного решения уравнений (154) и (155) с заменой перед N знака „минус” знаком „плюс”.
При косом внецентренном растяжении для определения положения границы сжатой зоны кроме использования формул (154) и (155) требуется соблюдение дополнительного условия, чтобы точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре лежали на одной прямой (см. черт. 45).
РАСЧЕТ СЕЧЕНИЙ,
НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
3.81. Расчет наклонных сечений внецентренно растянутых элементов на действие поперечной силы производится как для изгибаемых элементов согласно пп. 3.28¾3.41. При этом значение Mb в п. 3.31 определяется по формуле
(167)
где 
но не более 0,8;
значение Qb,min принимается равным jb 3 (1 + jf – jn) Rbtbh 0. Кроме того, во всех формулах пп. 3.29, 3.40 и 3.41 коэффициент jb 4 заменяется на jb 4 (1 – jn).
Расчет наклонных сечений внецентренно растянутых элементов на действие изгибающего момента производится как для изгибаемых элементов согласно пп. 3.42¾3.45. При этом высота сжатой зоны в наклонном сечении определяется с учетом растягивающей силы N по формуле (160) или согласно п. 3.80.
В случае выполнения условия e ¢ < h 0 – a ¢ расчетный момент в наклонном сечении допускается определять как момент всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно оси, проходлящей через центр тяжести арматуры S¢.
ПРИМЕРЫ РАСЧЕТА
Пример 42. Дано: растянутая ветвь двухветвевой колонны с поперечным сечением размерами b = 500 мм, h = 200 мм; а = а¢ = 40 мм; продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь ее сечения As = A¢s = 982 мм2 (2 Æ 25); бетон тяжелый класса В25 (Rb = 16 МПа при gb 2 = 1,1); продольная сила N = 44 кН; максимальный изгибающий момент М = 43 кН · м.
Требуется проверить прочность нормального сечения.
Расчет. h 0 = 200 – 40 = 160 мм;
мм;
мм;
мм.
Поскольку арматура симметричная, прочность проверим из условия (157):
т. е. условие (157) не удовлетворяется. Так как е ¢ = 1037 мм > h 0 – a ¢ = 120 мм, а высота сжатой зоны х, определенная по формуле (160) без учета сжатой арматуры:
согласно примечанию к п. 3.78 проверим прочность из условия (159), принимая х = 40 мм и A ¢ s = 0:
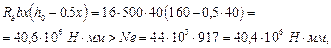
т. е. прочность нормального сечения обеспечена.
Пример 43. Дано: прямоугольное сечение размерами b = 1000 мм, h = 200 мм; а = а ¢ = 35 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа при gb 2 = 0,9); продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь сечения арматуры S¢ A ¢ s = 1005 мм2; растягивающая сила N = 160 кН; изгибающий момент М = 116 кН·м.
Требуется определить площадь сечения арматуры S.
Расчет. h 0 = 200 – 35 = 165 м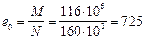м;
мм;
мм;
мм.
Так как е ¢ = 790 мм h 0 – а ¢ = 165 – 35 = 130 мм, определим необходимую площадь сечения растянутой арматуры согласно п. 3.79б.
Вычислим значение
Так как 0 < am < aR = 0,44 (см. табл. 18), значение As определим по формуле (163). Для этого по табл. 20 при am = 0б276 находим x = 0,33.
Принимаем As = 3079 мм2 (5 Æ 28).
Пример 44. Дано: прямоугольное сечение размерами b = 1000 мм, h = 200 мм; а = а¢ = 40 мм; бетон тяжелый класса В15 (Rb = 7,7 МПа при gb 2 = 0,9); продольная арматура класса A-III (Rs = Rsc = 365 МПа); растягивающая сила N = 532 кН; изгибающий момент М = 74 кН·м.
Требуется определить площадь сечения симметричной продольной арматуры.
Расчет. h 0 = h – a = 200 – 40 = 160 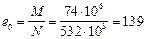мм;
мм;
мм;
мм.
Поскольку арматура симметричная, площадь сечения арматуры определим по формуле (161):
мм2.
Так как е ¢ = 199 мм > h 0 – а ¢ = 120 мм, согласно примечанию к п. 3.79 значение As можно снизить.
Определим значение x без учета сжатой арматуры. Для этого вычислим значение am:
Из табл. 20 при am = 0,213 находим x = 0,24 и z = 0,88. Так как 
определим значение As по формуле (165):
мм2.
Принимаем As = A ¢ s = 2281 мм2 (6 Æ 22).
Пример 45. Дано: растянутая ветвь двухветвевой колонны с сечением размерами b = 500 мм, h = 200 мм; а = а¢ = 40 мм; бетон тяжелый класса В25 (Rbt = 1,15 МПа при gb 2 = 1,1); хомуты, расположенные по граням ветви, из арматуры класса A-III (Rsw = 285 МПа); продольная растягивающая сила N = 44 кН; поперечная сила Q = 143 кН; расстояние между перемычками двухветвевой колонны l = 600 мм.
Требуется определить диаметр и шаг хомутов.
Расчет. h 0 = h – а = 200 – 40 = 160 мм. Расчет производим согласно п. 3.33а с учетом рекомендаций п. 3.81.
Значение Mb определим по формуле (167), приняв jb 2 = 2 (см. табл. 21), jf = 0 и 
0,096 < 0,8:
Н·мм.
Поскольку в пределах между перемычками поперечная сила постоянна, длину проекции наклонного сечения принимаем максимально возможной, т. е.
мм < l = 160 мм.
Тогда
Так как 2 h 0 = 2 · 160 = 320 мм < с = 533 мм, принимаем с 0 = 2 h 0 = 320 мм.
Определим коэффициент æ:
æ 
Поскольку 
1,667 < æ = 1,866 < 
3,33, интенсивность хомутов определим по формуле (63):
кН/м.
Максимально допустимый шаг хомутов, согласно п. 3.30, равен:
Кроме того, шаг хомутов, согласно п. 5.58, не должен превышать 2 h = 2 · 200 = 400 мм.
Принимаем шаг хомутов s = 100 мм < smax, тогда
мм2.
Принимаем два хомута диаметром по 10 мм (Asw = 157 мм2).
