Требуется подобрать вертикальные и горизонтальные поперечные стержни и проверить прочность ригеля на совместное действие кручения и изгиба.
Расчет. Поскольку сечение имеет входящие углы, проверим условие (184), разбив сечение на два прямоугольника размерами 800х320 и 155х250 мм и приняв Rb = 13 МПа (т.е. при 
= 0,9);
Н·мм > Т = 84 кН·м,
т.е. условие (184) удовлетворяется.
Расчет пространственных сечений производим как для прямоугольного сечения размерами b = 300 мм и h = 800 мм, так как нижняя грань ригеля и выступающая полка образуют угол.
Так как для опорного сечения 0,5 Qb =0,5·460·0,3=69 кН·м < Т=84 кН·м, согласно пп. 3.85 и 3.86, расчет приопорного участка по 1-й и 2-й схемам необходим.
Необходимую из расчета по 2-й схеме интенсивность вертикальных стержней определяем согласно п. 3.87.
Предварительно вычислим коэффициенты 
и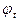 
:
;
где Аs2 = 1609 + 314 + 380 = 2304 мм2 (2Æ32 + Æ20 + Æ22).
Поскольку 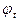< 1, интенсивность хомутов определим по формуле (182):
мм.
Принимая шаг вертикальных хомутов s 2 = 100 мм, находим площадь сечения одного хомута:
Asw2 = 1,54 · 100 = 154 мм2.
Принимаем хомуты диаметром 14 мм (Asw2 = 154 мм2).
Проверим прочность по продольной арматуре, установленной у верхней растянутой грани приопорного участка ригеля согласно п. 3.85а (1-я схема).
Из черт. 61, а находим As1 = 3217 мм2 (4Æ32) и 
= 1388 мм2 (2Æ20 + 2Æ22), а' = 68 мм.
По формуле (172) определим высоту сжатой зоны х1, принимая Rb = 16 МПа (т.е. при = 1,1, поскольку учитывается ветровая нагрузка):
мм > 2 а/ = 2 · 68 =
= 136 мм.
Шаг и диаметр горизонтальных поперечных стержней приопорного участка принимаем такими же, как для вертикальных хомутов, т.е. s 1=100 мм, Asw1 =154 мм2, отсюда
Н/мм;
h 0 = 800 - 80 = 720 мм.
Проверим выражение qsw1b (h0 -0,5 x1) = 446,6·300(720-0,5·139)=
= 87,2·106 Н·мм < 
Н·мм. Следовательно, qsw оставим без изменения.
Проверим условие (173):
<
< RsAs (ho -0,5 x1)=365·3217(720-0,5·139)=763,8·106 Н·мм,
т.е. верхней продольной арматуры из условия прочности установлено достаточно.
Из условия (176) проверим прочность по горизонтальной поперечной арматуре, расположенной на приопорном участке:
qsw1b(h0 - 0,5x1) = 446,6·300(720-0,5·139)=87,2·106 Н·м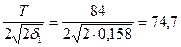м > 
кН·м,
т.е. горизонтальной поперечной арматуры на приопорном участке установлено достаточно.
Как видно из черт. 61, б, д, в сечении с наибольшим пролетным изгибающим моментом имеет место крутящий момент, поэтому следует проверить прочность по продольной арматуре, установленной у нижней растянутой грани в средней части пролета ригеля, из условия (174).
Для этой части ригеля, два верхних стержня Æ 32 оборваны, и поэтому, согласно черт: 61, а, имеем A/sw = 1609 мм2 (2 Æ 32); а/ = 62 мм; As1 = 1388 мм2 (2 Æ 20 + 2 Æ22); а = 68 мм.
Определим высоту сжатой зоны х1, принимая Rb = 13 МПа (т.е. при 
=0,9, поскольку ветровая нагрузка не учитывается):
< 0.
Принимаем х1 = 2а', отсюда h0 - 0,5 x1 = h - a - a' = 800 - 68 - 62 = 670 мм.
Горизонтальные поперечные стержни в средней части пролета принимаем диаметром 14 мм (Аsw1 = 154 мм2) и с шагом s1 = 200 мм, отсюда
Н/мм.
Из черт. 61, б, д имеем:
кН·м;
Мmax = 321 кН·м.
Проверим условие (174):
<
< RsAs1 (h0 - 0,5 x 1) = 365·1388·670=339,4·106 Н·мм,
т.е. нижней продольной арматуры из условия прочности установлено достаточно.
Определим, на каком расстоянии lх от нулевой точки эпюры Т можно допустить шаг горизонтальных поперечных стержней 200 мм, используя условие (176). Принимая Т=tlx, имеем qsw1b(h0 - 0,5 x1) = 
, отсюда
Следовательно, шаг горизонтальных стержней 100 мм можно допустить на приопорных участках ригеля длиной 2,45-1,47 
1 м.
Пример 47. Дано: балка перекрытия с поперечным сечением - по черт. 62, а; расположение нагрузок, эпюры изгибающих и крутящих моментов, а также эпюра поперечных сил - по черт. 62, б; бетон тяжелый класса В25 (Rb = 13 МПа при 
= 0,9); продольная и поперечная арматура класса А-III (Rs = Rsc = 365 МПа; Rsw - 290 МПа).
Требуется проверить прочность балки на совместное действие кручения и изгиба.
Расчет. Разбиваем поперечное сечение на два прямоугольника размерами 200х400 и 350х400 мм и проверяем условие (184):
= 84,5·106 Н·мм > Т = 40 кН·м.
