Пересечение плоскостью поверхности вращения. В сечении тела вращения плоскостью получается плоская кривая линия. Обычно ее строят по отдельным точкам, которые затем соединяют между собой плавной кривой по лекалу.
Точки, по которым строится кривая, разделяют на характерные (их называют особыми, опорными) и промежуточные.
К характерным относятся:
– крайние (самая верхняя и самая низкая, правая и левая, дальняя и ближняя); точки границы видимости – отделяющие видимую часть кривой от невидимой;
– точки, лежащие на контурах пересекающихся тел;
– концы осей эллипса и вершин параболы и гиперболы.
Когда характерные точки отстоят далеко друг от друга, то для более точного выявления хода кривой строят промежуточные точки, которые выбираются произвольно. Следует иметь в виду, что нередко заранее известна форма кривой, получающейся в сечении.
Сфера. Линия сечения сферы представляет собой окружность. Плоскость, проходящая через центр сферы, пересекает ее по кругу. По мере удаления секущей плоскости от центра сферы диаметр круга, получающегося в сечении, уменьшается.
 Задача 7.5. Даны секущая плоскость Σ(Σ2), сфера.
Задача 7.5. Даны секущая плоскость Σ(Σ2), сфера.
Построить сечение сферы плоскостью (рис. 7.13).
Алгоритм решения.
1. Отметить характерные точки А и В (А2 и В2), которые лежат на главном меридиане сферы.
2. Найти горизонтальные проекции (А1 и В1), опуская перпендикуляры линий связи до пересечения с горизонтальной осевой линией на П1.
3. Отметить точки 2 и 2`, лежащие на экваторе сферы. Горизонтальные проекции точек 2 и 2` находим, опуская перпендикуляры линий связи до пересечения с горизонтальным очерком сферы.
4. Определить ряд точек, лежащих между точками А и В, например, точки 1, 1` и
3, 3`. Их горизонтальные проекции можно построить при помощи метода вспомогательных секущих плоскостей:
– провести вспомогательную плоскость Р через точку 1 и 1`. Линия пересечения плоскости Р и сферы будет представлять собой окружность, радиус которой равен расстоянию от осевой линии до очерка сферы;
– радиусом R1 на горизонтальной проекции построить окружность (линию пересечения плоскости Р со сферой);
– найти точки 1 и 1`, опуская перпендикуляры линий связи из точек 12 и 1`2 до пересечения с окружностью линии пересечения. В результате получаются точки 11 и 1`1. Точки 3 и 3` строятся аналогично.
5. Соединить по порядку полученные точки А1, 11, 21, 31, В1, 3`1, 2`1, 1`1, которые принадлежат линии проекции контура сечения.
Цилиндр вращения пересекается плоскостью по окружности, если плоскость перпендикулярна оси; по эллипсу – во всех остальных случаях. При пересечении цилиндра вращения плоскостью, параллельной оси вращения, получается пара прямых.
Если секущая плоскость перпендикулярна оси вращения, то в результате сечения цилиндра этой плоскостью получится окружность.
В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получится эллипс.
 Задача 7.6. Даны плоскость Δ(Δ2), цилиндр вращения.
Задача 7.6. Даны плоскость Δ(Δ2), цилиндр вращения.
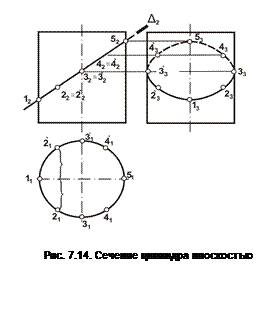
Построить сечение цилиндра плоскостью (рис. 7.14).
Алгоритм решения.
1.Обозначить концы осей эллипса: большой – точки 1 и 5, малой – точки 3 и 3`.
2. Отметить точки 1,5, 3, 3` на горизонтальной и профильной проекции цилиндра. На плоскости П1 эти точки лежат на линии окружности основания. На плоскости П3 точки 1 и 5 лежат на вертикальной оси симметрии, а точки 3 и 3` – на крайних образующих.
3. Построение проекций промежуточных точек эллипса, которых должно быть 10–12, показано на примере точек 2, 2`, 4, 4`.
4. Соединить полученные точки эллипса на профильной проекции с учетом видимости. На горизонтальной проекции контур эллипса совпадает с контуром основания цилиндра.
Задача 7.7. Даны плоскость P(P1) и конус вращения.
Построить сечение конуса плоскостью (рис. 7.15).

|
| Рис. 7.15. Сечение конуса вращения плоскостью |
Алгоритм решения.
плоскость Р и ось вращения конуса перпендикулярны к плоскости П1, следовательно, они параллельны между собой и заданная плоскость Р пересекает коническую поверхность по гиперболе. Фигура сечения представляет собой часть плоскости, ограниченной гиперболой и замыкающей ее хордой.
1. На горизонтальной проекции конуса определить точки 1, 3, 4 (11, 31, 41):
– точки 1 и 4 являются границами хорды, по которой Р пересекает основание конуса;
– точка 3 – вершина гиперболы. Она находится в середине горизонтальной проекции фигуры сечения.
2. Найти фронтальные и профильные проекции точек 1, 3, 4:
– точки 1 и 4 проецируем на основание конуса на фронтальную и профильную его проекции;
– точку 3 находим с помощью образующей. Строим остальные точки гиперболы 2 и 5;
– точка 52 лежит на очерковой образующей;
– точка 53 – на осевой линии профильной проекции конуса;
– точка 22 лежит на осевой линии фронтальной проекции;
– 23 лежит на очерковой образующей профильной проекции. На фронтальной проекции соединяем точки 12, 22,32,52,42 с учетом видимости;
– на профильной проекции соединить точки 13, 23, 33, 53, 43.
3. Изобразить профильную проекцию гиперболы линией невидимого контура, так как построенная проекция находится на той части конуса, которая невидима.
Пересечение гранной поверхности плоскостью. Геометрическая фигура, получающаяся в результате пересечения многогранника плоскостью, называется сечением многогранника. Сечение представляет собой плоский многоугольник с внутренней областью. В частном случае эти многоугольники могут распадаться на несколько многогранников, вырождаться в прямые и точки.
Задача 8. Даны плоскость Σ(Σ2) и пирамида SABC.
Построить сечение пирамиды плоскостью (табл. 7.3).
Таблица 7.3






