| Словесная форма | Графическая форма |
| 1. Построить горизонталь h в плоскости Р(АВС): – через точку А2 провести фронтальную проекцию горизонтали h2; – построить горизонтальную проекцию горизонтали | 
|
| 2. Принять горизонталь за ось вращения, при котором точки A и D остаются неподвижны, а вершины В и С вращаются по окружности. 3. Определить радиус вращения для точки В методом прямоугольного треугольника: – из точки В1 провести перпендикуляр к h1, B1n1 ^ h1; – определить ΔΖ для отрезка Bn | 
|
Окончание табл. 6.4
| Словесная форма | Графическая форма |
| 3. Построить точку В0: – радиусом Rb провести дугу до пересечения с перпендикуляром B1n1. 4. Построить точку С0: – из С1 провести перпендикуляр к h1 (A1D1); – определить точку С0 на пересечении прямой B0D1 с траекторией ее вращения | 
|
| 5. Соединить полученные точки в треугольник А1В0С0, которые определяют натуральную величину треугольника, А1В0С0 = IABCI | 
|
& Рекомендуемый библиографический список [2–11].
7. Комплексный чертЁж поверхностей
Определение поверхности
В начертательной геометрии фигуры задаются графически, поэтому целесообразно дать следующее определение поверхности.
Поверхность – это множество всех последовательных положений линии, движущейся по определенному закону.Линия может быть прямой, либо кривой. Непрерывно перемещающаяся линия называется образующей(рис. 7.1); неподвижные линии, по которым движется образующая при образовании поверхности, – направляющими(рис. 7.1). Направляющих может быть одна и более линий.

| 
|
| Рис. 7.1. Элементы поверхностей: l – образующая; m – направляющая |
Задание поверхности на комплексном чертеже
Для построения проекций поверхности или тела, ограниченного поверхностью, обычно не строят всех её точек, а определяют только очерк поверхности (рис. 7.2).
| |||
| |||
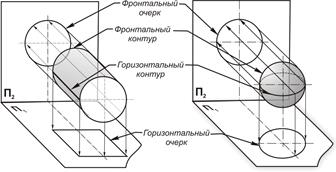
Рис. 7.2. Построение проекций поверхностей: а – цилиндрической; б – сферы
Очерком поверхности называют линию, ограничивающую проекцию фигуры на плоскости проекций. Проекции любой точки поверхности лежат внутри очерка (в частном случае на очерке). Если линией контура поверхности служит образующая поверхности, то её называют контурной образующей, а её проекцию – очерковой образующей.
При построении эпюра поверхности направление проецирования совпадает с направлением взгляда наблюдателя, поэтому контурная линия является границей видимости поверхности: та её часть, которая расположена перед линией контура, – видима, остальная – невидима.
Очерковая линия разделяет проекцию на видимую и невидимую части. Проекции точек поверхности, расположенные на очерках, будем называть точками перемены (границы) видимости. Невидимые точки принято обозначать в скобках.
7.3. Классификация поверхностей
Многообразие форм поверхностей создает большие трудности при их изучении. Для того чтобы обеспечить процесс изучения поверхностей, необходимо их систематизировать. К сожалению, невозможно разработать универсальную классификацию поверхностей. Внутри каждого способа образования поверхностей существует своя база для систематизации, например, в кинематическом способе образования поверхностей в основе систематизации лежит вид образующей и закон ее перемещения. Одна из возможных классификаций представлена на рис. 7.3.

Рис. 7.3. Классификация поверхностей
Линейчатые поверхности. Поверхности, которые образуются при некотором закономерном движении прямой в пространстве, называются линейчатыми. Линейчатые поверхностив общем случае однозначно определяются тремя направляющими линиями m, n, f.
Линейчатые поверхности делятся на развёртывающиеся и неразвёртывающиеся. Развертывающиеся поверхности могут без деформации (складок и разрывов) совмещаться с плоскостью. К наиболее распространенным развёртывающимся поверхностям относятся: цилиндрические, конические, с ребром возврата (торса), призматические, пирамидальные.
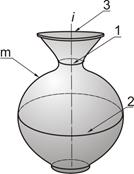
Поверхности вращения общего вида. Поверхности вращения общего вида –это поверхности, образованные произвольной линией (образующей l) при ее вращении вокруг неподвижной оси (оси поверхности i).
При задании поверхности вращения на комплексном чертеже ось вращения i располагают перпендикулярно одной из плоскостей проекций. Элементы поверхности: m – главный меридиан, 1 – горло, 2 – экватор
(рис. 7.4, а). В этом случае все параллели поверхности, горло 1 и экватор 2 проецируются на П1 в истинную величину, а на П2 – в отрезки прямых, перпендикулярные i2 – проекции оси i. Для задания поверхности вращения общего вида на комплексном чертеже строят проекции главного меридиана m1 и m2, проводят проекции горла, экватора и двух параллелей (7.5, б).
|

| ||||||||
| Рис. 7.4. Поверхность вращения общего вида: а – наглядное изображение; б – комплексный чертеж; 1 – горло; 2 – экватор; m – главный меридиан |
Свойства поверхностей вращения.
1. Вращаясь вокруг своей оси, поверхность может сдвигаться без деформации вдоль самой себя.
2. Если меридиан поверхности вращения проходит через две точки поверхности, то он является кратчайшей линией между этими точками и все меридианы равны между собой.
3. Каждая из параллелей поверхности вращения пересекает меридиан под прямым углом, т. е. параллели и меридианы образуют прямоугольную сеть на поверхности вращения.
4. Поверхность вращения можно задать кривой, если эта кривая пересекает все ходы точек образующей линии.
Линейчатые развертываемые поверхности вращения. Линейчатые развертываемые поверхности вращения – это поверхности, образованные вращением прямолинейной образующей l вокруг неподвижной оси поверхности I по кривой или ломаной направляющей m, развертки которых можно совместить с плоскостью без разрывов и складок.
К наиболее распространенным линейчатым развертываемым поверхностям вращения относятся: цилиндр вращения, конус вращения, однополостный гиперболоид (табл. 7.1).
Таблица 7.1