 Чтобы задать на чертеже проекции точек, принадлежащих, многограннику или кривой поверхности, необходимо предварительно построить какую-либо линию на заданной поверхности, а затем на проекциях этой линии взять проекции искомых точек. В качестве таких линий, принадлежащих, например, поверхностям вращения, могут быть выбраны образующие, параллели, меридианы и др. В ряде случаев, если образующая поверхность тела прямая – проецирующая, то отсутствующие на чертеже проекции точек могут быть найдены без дополнительных построений.
Чтобы задать на чертеже проекции точек, принадлежащих, многограннику или кривой поверхности, необходимо предварительно построить какую-либо линию на заданной поверхности, а затем на проекциях этой линии взять проекции искомых точек. В качестве таких линий, принадлежащих, например, поверхностям вращения, могут быть выбраны образующие, параллели, меридианы и др. В ряде случаев, если образующая поверхность тела прямая – проецирующая, то отсутствующие на чертеже проекции точек могут быть найдены без дополнительных построений.
Задача 7.1. Дана цилиндрическая поверхность, фронтальные проекции точек А, В и С (А2, В2 и С2).
Построить горизонтальные проекции точек А, В, С, принадлежащих цилиндрической поверхности (рис. 7.9).
Алгоритм решения.
1. все образующие цилиндра перпендикулярны к П1, в этом случае горизонтальные проекции всех точек, расположенных на этой поверхности, находятся на горизонтальной (вырожденной) проекции поверхности.
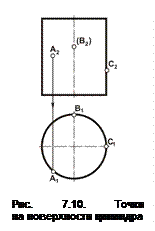 2. Опустить линии связи на П1 и отметить проекции точек А1, В1 и С1, учитывая, что точка B находится на невидимой части поверхности при взгляде на П2.
2. Опустить линии связи на П1 и отметить проекции точек А1, В1 и С1, учитывая, что точка B находится на невидимой части поверхности при взгляде на П2.
В случае, если заданы горизонтальные проекции точек на данной поверхности, то положение их фронтальных проекций не определено.
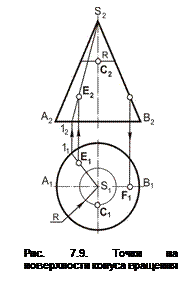
Задача 7.2. Дан конус вращения, проекции точек F(F2), E(E1) и С(С2).
Построить проекции точек E(E2), F(F1), C(C1) (рис. 7.10).
Алгоритм решения.
1. Точка F принадлежит фронтальной очерковой образующей SА (S2А2): опустить проекцию точки F(F1) на горизонтальную проекцию одноимённой образующей S1А1.
2. Для построения точки E(E2):
– через проекцию E1 провести образующую S1 (S111);
– построить проекцию образующей на П2 – 12S2;
– на проекции линии 12S2 отметить точку Е2.
3. Для построения точки С(С1):
– через проекцию С2 провести параллель параллельно А2В2;
 – построить проекцию параллели на П1 – окружность радиусом R (величина радиуса R определяется по фронтальной проекции).
– построить проекцию параллели на П1 – окружность радиусом R (величина радиуса R определяется по фронтальной проекции).
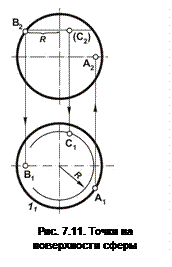
Задача 7.3. Дана сфера, проекции точек А(А1), В(В2) и С(С2) Построить проекции точек А(А2), В(В1) и С(С1) (рис. 7.11).
Алгоритм решения.
1. Точка А принадлежит экватору сферы, фронтальную проекцию точки отметить на проекции одноимённой линии.
2. Точка В принадлежит главному меридиану сферы, горизонтальную проекцию точки отметить на проекции одноимённой линии.
3. построение точки С(С1).
3.1. Через проекцию С2 провести параллель – прямую, параллельную экватору.
3.2. Построить проекцию параллели на П1 – окружность радиуса R (величина радиуса R определяется по фронтальной проекции).
3.3. Отметить проекцию С1 на проекции параллели.
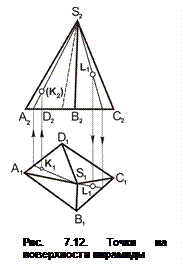 Задача 7.4. Дана пирамида, проекции точек К(К1) и L(L2).
Задача 7.4. Дана пирамида, проекции точек К(К1) и L(L2).
Построить проекции точек K(K2), L(L1) (рис. 7.12).
Алгоритм решения.
1. Для построения точки К(К2):
– через проекцию К1 провести образующую;
– построить проекцию образующей на П2;
– отметить проекцию точки К(К2) на П2.
2. Для построения точки L(L1):
– через проекцию L2 провести образующую;
– построить проекцию образующей на П1;
– отметить проекцию точки L(L1) на П1.
Возможно построение недостающих проекций точек с помощью вспомогательных прямых – горизонталей, например, через проекцию точки К – К1 провести h1 II А1D1, затем построить h2, а на ней – точку К2. На проекции параллели отметить точку С1.






