Точка[11] – одно из основных понятий геометрии. В современной математике точками называют элементы различной природы, из которых состоят пространства, например, в евклидовом пространстве точкой называют упорядоченную совокупность из n чисел.
В начертательной геометрии положение точки в пространстве можно определить её координатами. Замечательным признаком является то, что координата, характеризующая удаление точки от плоскости проекций, одноимённа с осью, которая не присутствует при образовании этой плоскости проекций. Так, удаление точки от П2 измеряется координатой y, а сама фронтальная плоскость проекций П2 образуется пересечением осей OХ и OZ.
Таким образом, каждая из трёх проекций точки характеризуется двумя координатами, их название соответствует названиям осей, которые образуют соответствующую плоскость проекций: горизонтальная – A1(XA; YA); фронтальная – A2(XA; ZA); профильная – A3(YA; ZA).
Трансляция координат между проекциями осуществляется с помощью линий связи. Так, в системе плоскостей проекций П1П2 общая для фронтальной и горизонтальной проекций координата x транслируется вертикальной линией связи А2А1, перпендикулярной оси OХ.
По двум данным проекциям можно построить проекции точки либо с помощью координат, либо графически. Графически профильную проекцию строят, транслируя параметр Z горизонтальной линией связи, проведённой из фронтальной проекции, а параметр Y переносят с горизонтальной проекции, используя постоянную прямую чертежа k – биссектрису угла расщеплённой оси: Y1ОY3, на которой горизонтальная линия связи, проведённая из горизонтальной проекции перпендикулярно OY1, преломляется под прямым углом. При этом у начала координат формируется квадрат со стороной, равной координате Y оригинала, что обеспечивает передачу координаты Y между горизонтальной и профильной проекциями. В табл. 3.1 и 3.2 представлены общие алгоритмы построения точки А по координатам в пространственной модели системы трёх плоскостей проекций П1П2П3 и на комплексном чертеже.
Таблица 3.1
| Алгоритм построения наглядного изображения точки по координатам | |
| Словесная форма | Графическая форма |
| 1. Отложить на осях X, Y, Ζ соответствующие координаты точки А. Получим точки Ax, Ay, Az | 
|
| 2. Горизонтальная проекция А1 находится на пересечении линий связи из точек Ax и Ay, проведенных параллельно осям X и Y | 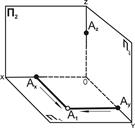
|
| 3. Фронтальная проекция А2 находится на пересечении линий связи из точек Ax и Az, проведенных параллельно осям X и Ζ | 
|
| 4. Профильная проекция А3 находится на пересечении линий связи из точек Ay и Az, проведенных параллельно осям Y и Ζ | 
|
| 5. Точка А находится на пересечении линий связи, проведенных из точек А1, А2 и А3 | 
|
Таблица 3.2
Алгоритм построения комплексного чертежа
точки по координатам
| Словесная форма | Графическая форма |
| 1. Отложить на осях X, Y, Ζ соответствующие координаты точки А. Получаем точки Ax, Ay, Az | 
|
| 2. Горизонтальная проекция А1 находится на пересечении линий связи из точек Ax и Ay, проведенных параллельно осям X и Y | 
|
| 3. Фронтальная проекция А2 находится на пересечении линий связи из точек Ax и Az, проведенных параллельно осям X и Ζ | 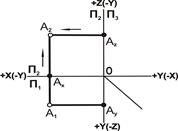
|
| 4. Профильная проекция А3 находится на пересечении линий связи из точек Az и Ay, проведенных параллельно осям Ζ и Y | 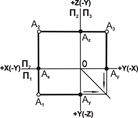
|






