Две прямые в пространстве могут быть параллельными, пересекаться и скрещиваться.
Параллельные прямые. Если прямые параллельны, то их одноименные проекции параллельны[12] (рис. 4.10). Если ABIICD, то [A1B1]II[C1D1]; [A2B2]II[C2D2]; [A3B3]II[C3D3] (рис. 4.10). В свою очередь, если проекции прямых линий на всех плоскостях проекций параллельны, то прямые линии параллельны.
Особый случай представляют собой прямые линии, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых линий параллельны, но для оценки их взаимного положения необходимо построить профильные проекции прямых, которые
в рассмотренном случае на плоскости П3 пересекаются, следовательно, AB
и CD не параллельны [A1B1]II[C1D1]; [A2B2]II[C2D2]; [A3B3]∩[C3D3] (рис. 4.11).

| 
| ||||
| Рис. 4.10. Прямые линии, параллельные: а – наглядное изображение; б – комплексный чертёж | |||||

|

| ||||
| Рис. 4.11. Прямые линии, непараллельные: а – наглядное изображение; б – комплексный чертёж |
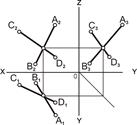
Пересекающиеся прямые. Если прямые пересекаются, то их проекции также пересекаются, а точки пересечения проекций находятся в проекционной связи[13] (рис. 4.12). Рассмотрим два частных случая.

| 
| |||||
| Рис. 4.12. Прямые линии пересекающиеся: а – наглядное изображение; б – комплексный чертёж | ||||||

| 
| |||||
| Рис. 4.13. Прямые линии не пересекаются | Рис. 4.14. Прямые линии пресекаются | |||||
1. Если одна из прямых параллельна какой-либо плоскости проекций, например, профильной, то по двум проекциям невозможно судить об их взаимном расположении (рис. 4.13).
2. Пересекающиеся прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций. О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции [А1В1]∩[С1D1]Þ АВ∩СD (рис. 4.14).
Скрещивающиеся прямые. Если одна из двух прямых линий лежит в некоторой плоскости, а другая прямая линия пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые – скрещивающиеся (рис. 4.15).

|

| ||||
| Рис. 4.15. Прямые линии скрещивающиеся: а – наглядное изображение; б – комплексный чертёж |
Взаимное положение точки и прямой линии
1. Если точка принадлежит прямой линии, то её проекции принадлежат одноимённым проекциям этой прямой линии: C Ì lÞC1 Ì l1, C2 Ì l2 (рис. 4.16).
2. Если точка не принадлежит прямой линии, то по крайней мере, одна из её проекций не принадлежит одноимённой проекции прямой: А, В и D не принадлежат прямой l, причем точка D расположена над прямой, а точка В – перед прямой.


Рис. 4.16. Взаимное положение прямой линии и точек: а – наглядное изображение; б – комплексный чертёж
Выводы по теме
1. Для получения комплексного чертежа прямой линии, достаточно построить проекции точек и соединить их одноимённые проекции прямыми линиями.
2. Прямая линия относительно плоскостей проекций занимает общее положение и частное.
3. Прямые частного положения – это прямые, которые параллельны, либо перпендикулярны одной из плоскостей проекций.
4. Прямые уровня – прямые, параллельные одной из плоскостей проекций. Различают три основные линии уровня: горизонтальную, фронтальную и профильную прямые.
5. Проецирующие прямые – это прямые, перпендикулярные плоскости проекций. Различают три основные проецирующие линии: горизонтально проецирующую, фронтально проецирующую и профильно проецирующую прямые.
6. Прямые линии в пространстве могут быть параллельны, пересекаться и скрещиваться.
7. Точка принадлежит прямой линии, если её проекции принадлежат одноименным проекциям прямой.
Ключевые слова
· Прямая линия
· Прямая линия общего положения
· Прямые уровня (горизонталь, фронталь, профильная прямая)
· Проецирующие прямые
· Параллельные прямые
· Пересекающиеся прямые
· Скрещивающиеся прямые






