Рассмотрим три варианта взаимного расположения точек в зависимости от соотношения координат, определяющих их положение в пространстве.
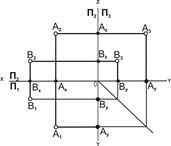
1. На рис. 3.4 точки A и B имеют различные координаты.

| 
| ||||
| Рис. 3.4. Варианты взаимного расположения точек: а – наглядное изображение; б – комплексный чертёж |
Их взаимное расположение можно оценить по удаленности к плоскостям проекций: YА>YВ, тогда точка A расположена дальше от плоскости П2 и ближе к наблюдателю, чем точка B; ZА>ZВ, тогда точка A расположена дальше от плоскости П1 и ближе к наблюдателю, чем точка B; XА<XВ, тогда точка B расположена дальше от плоскости П3 и ближе к наблюдателю, чем (при взгляде слева) точка А.
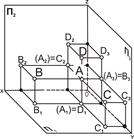
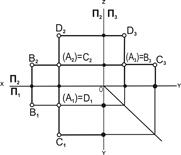
2. На рис. 3.5 представлены точки A, B, С, D, у которых одна из координат совпадает, а две другие отличаются.
| 
| ||||
| Рис. 3.5. Конкурирующие точки: а – наглядное изображение; б – комплексный чертёж |
Их взаимное расположение можно оценить по удалённости к плоскостям проекций следующим образом:
YА=YВ=YD, то точки А, В и D равноудалены от плоскости П2, и их горизонтальные и профильные проекции расположены соответственно на прямых [А1В1]llОХ и [А3В3]llOZ. Геометрическим местом таких точек служит плоскость, параллельная П2;
ZА=ZВ=ZС, то точки А, В и С равноудалены от плоскости П1, и их фронтальные и профильные проекции расположены соответственно на прямых [А2В2]llОХ и [А3С3]llOY. Геометрическим местом таких точек служит плоскость, параллельная П1;
XА=XC=XD, то точки А, C и D равноудалены от плоскости П3 и их горизонтальные и фронтальные проекции расположены соответственно на прямых [А1C1]llOY и [А2D2]llOZ. Геометрическим местом таких точек служит плоскость, параллельная П3.
3. Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рис. 3.3 даны три пары таких точек, у которых: XА=XD; YА=YD; ZD > ZА; XA=XC; ZA=ZC; YC > YA; YA=YB; ZA=ZB; XB > XA.
Различают горизонтально конкурирующие точки А и D, расположенные на горизонтально проецирующей прямой АD, фронтально конкурирующие точки A и C, расположенные на фронтально проецирующей прямой AC, профильно конкурирующие точки A и B, расположенные на профильно проецирующей прямой AB.
Выводы по теме
1. Точка – линейный геометрический образ, одно из основных понятий начертательной геометрии. Положение точки в пространстве можно определить её координатами. Каждая из трёх проекций точки характеризуется двумя координатами, их название соответствует названиям осей, которые образуют соответствующую плоскость проекций: горизонтальная – A1(XA; YA); фронтальная – A2(XA; ZA); профильная – A3(YA; ZA). Трансляция координат между проекциями осуществляется с помощью линий связи. По двум проекциям можно построить проекции точки либо с помощью координат, либо графически.
3. Точка по отношению к плоскостям проекций может занимать в пространстве как общее, так и частное положение.
4. Точка общего положения – точка, не принадлежащая ни одной
из плоскостей проекций, т. е. лежащая в пространстве между плоскостями проекций. Координаты точки общего положения не равны нулю (x≠0,y≠0,z≠0).
5. Точка частного положения – это точка, принадлежащая одной или двум плоскостям проекций. Одна из координат у точки частного положения равна нулю, поэтому проекция точки лежит на соответствующем поле плоскости проекций, другие две – на осях проекций.
6. Конкурирующие точки – точки, одноименные координаты которых совпадают. Существуют горизонтально конкурирующие точки, фронтально конкурирующие точки, профильно конкурирующие точки.
Ключевые слова
· Точка
· Координаты точки
· Точка общего положения
· Точка частного положения
· Конкурирующие точки






