Алгоритм построения проекций отрезка прямой линии

Словесная форма	Графическая форма
1. Отложить значения координат для точек А и В на осях x, y, z. Получаем вспомогательные точки: Ax, Bx на оси OX; Aу, By на оси OY; Az Bz на оси OZ. При построении этих точек необходимо учитывать знаки координат и откладывать их на осях в соответствующем направлении
2. Построить проекции точек А и В: А1(x; y), В1(x; y); А2(x; z), В2 (x;z). 3. Соединить соответствующие проекции точек А1 с В1, А2 с В2. Получаем проекции отрезка АВ: [А1В1] и [А2В2]. [А1В1] – это проекция отрезка прямой линии на П1. [А2В2] – это проекция отрезка прямой линии на П2
4. Отложить значение координаты Y на оси OY профильной плоскости: Ay By, где A3(y; z), B3 (y; z)

4.2. Положение прямой линии относительно
плоскостей проекций

По положению прямой линии относительно плоскостей проекций различают прямые общего положения и частного положения (рис. 4.1).

Рис. 4.1. Классификация прямых линий

 

Прямая линия общего положения не параллельная ни одной из плоскостей проекций. В системе плоскостей проекций П₁П₂П₃ прямая АВ будет иметь следующие проекции: [А₁В₁] на П₁, [А₂В₂] на П₂, и [А₃В₃] на П₃ (рис. 4.2).

 

а	б
Рис. 4.2. Прямая линия общего положения: а – наглядное изображение; б – комплексный чертёж

Прямая линия частного положения – прямая, параллельная либо перпендикулярная одной из плоскостей проекций.

Прямая линия уровня – прямая, параллельная одной из плоскостей проекций: горизонтали, фронтали, профильной прямой.

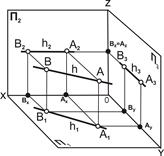
Горизонталь h – прямая линия, параллельная горизонтальной плоскости проекций П₁ (рис. 4.3).

Свойства проекций горизонтали.

1. Проекция прямой линии h₁(A₁B₁) равна самому отрезку, [A₁B₁]=|AB|.

2. Фронтальная и профильная проекции параллельны осям проекций, h₂[А₂В₂]II Ox, [A₃B₃]IIOY.

3. Угол наклона β к плоскости П₂ проецируется в натуральную величину на плоскость П₁.

4. На комплексном чертеже определяется двумя проекциями h₁, h₂.

 

а	б
Рис. 4.3. Горизонталь h: а – наглядное изображение; б – комплексный чертёж

Фронталь f – прямая линия, параллельная фронтальной плоскости проекций П₂ (рис. 4.4).

Свойства проекций фронтали.

1. Проекция фронтали f₂(A₂B₂) равна самому отрезку, [A₂B₂]=|AB|.

2. Горизонтальная и профильная проекции параллельны осям проекций: [А₁В₁]II Ox,[A₃B₃]IIOZ.

3. Угол наклона a к плоскости П₁ проецируется в натуральную величину на плоскость П₂.

4. На комплексном чертеже определяется двумя проекциями f₁, f₂.

 

а	б
Рис. 4.4. Фронталь f: а – наглядное изображение; б – комплексный чертёж

Профильная прямая р – это прямая линия, параллельная профильной плоскости проекций П₃ (рис. 4.5).

Свойства проекций профильной прямой.

1. Проекция профильной прямой p₃(A₃B₃) равна самому отрезку, [A₃B₃]=|AB|.

2. Горизонтальная и фронтальная проекции параллельны осям проекций: [А₁В₁]II y, [A₂B₂]IIOZ.

3. Углы наклона a и β проецируются в натуральную величину на плоскость П₃.

4. На комплексном чертеже определяется двумя проекциями p₂, p₃.

 

а	б
Рис. 4.5. Профильная прямая p: а – наглядное изображение; б – комплексный чертёж

Проецирующая прямая линия – это прямая, перпендикулярная плоскости проекций.

Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций П₁ (рис. 4.6).

 

а	б
Рис. 4.6. Горизонтально проецирующая прямая: а – наглядное изображение; б – комплексный чертёж

 

Свойства проекций горизонтально проецирующей прямой.

1. Проекция прямой линии m₂(A₁B₁) вырождается в точку, А₁=В₁.

2. Проекция m₂(А₂В₂) параллельна линиям связи.

3. Горизонтально проецирующая прямая параллельна одновременно П₂ и П₃, следовательно, [А₂В₂] = [А₃В₃] = |АВ|.

Фронтально проецирующая прямая – прямая линия, перпендикулярная фронтальной плоскости проекций П₂ (рис. 4.7).

 

а	б
Рис. 4.7. Фронтально проецирующая прямая: а – наглядное изображение; б – комплексный чертёж

 

Свойства проекций фронтально проецирующей прямой.

1. Проекция прямой линии i₂(С₂D₂) вырождается в точку, C₂=D₂.

2. Проекция i₁(С₁D₁) и проекция i₃(С₃D₃) параллельны линиям связи.

3. Фронтально проецирующая прямая параллельна одновременно П₁ и П₃, следовательно, [C₁D₁] = [C₃D₃] = |CD|.

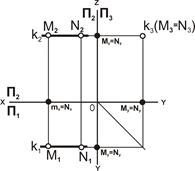
Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций П₃ (рис. 4.8).

 

а	б
Рис. 4.8. Профильно проецирующая прямая: а – наглядное изображение; б – комплексный чертёж

Свойства проекций профильно проецирующей прямой.

1. Проекция прямой линии k₃(M₃N₃) вырождается в точку, M₃=N₃.

2. Горизонтальная k₁(M₁N₁) и фронтальная k₂(M₂N₂) проекции перпендикулярны линиям связи.

3. Профильно проецирующая прямая параллельна одновременно П₁ и П₂, следовательно, [M₂N₂] = [M₁N₁] = |MN|.