Производные порядка выше первого называются производными высших порядков.
Рассмотрим явно заданную функцию 
.
Производная этой функции 
– функция, зависящая от 
. Если функция 
дифференцируема, то её производная называется производной второго порядка и обозначается 
или 
.
Следовательно,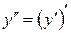 
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается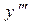 
. Следовательно, 
.
Производной n - го порядка (или n -й производной) называется производная от производной 
порядка:
.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (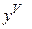
или 
– производная пятого порядка).
Пример. Найти производную 
-го порядка от функции 
.
Решение:
,
,
,
,
…………….,
.
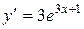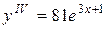Ответ: .
Рассмотрим функцию заданную неявно в виде уравнения 
.
Первую производную от неявной функции можно найти по формуле 
. Так как первая производная 
выражается через неявную функцию, то при её повторном дифференцировании нужно учитывать, что 
.
Пример. Найти производную второго порядка от функции 
.
Решение: Дифференцируем уравнение по .
. Далее имеем:
.
Ответ: 
.
Рассмотрим функцию заданную параметрически:
Как известно, первая производная 
находится по формуле 
.
Найдем вторую производную от функции заданной параметрически. Из определения второй производной и формулы следует, что
, т.е.
. (2.4.1)
Аналогично получаем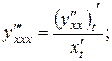 
…, 
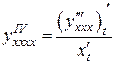и т.д.
Пример. Найти производную второго порядка от функции
Решение: 
.
Тогда по формуле (2.4.1) 
.
Ответ: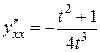 
.
Пусть материальная точка 
движется прямолинейно по закону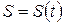 
. Как уже известно, производная 
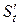равна скорости точки в данный момент времени: 
.
Пусть в момент времени 
скорость точки равна 
, а в момент 
– скорость равна 
, т.е. за промежуток времени 
скорость изменилась на величину 
.
Отношение 
выражает среднее ускорение движения точки за время . Предел этого отношения при 
, называется ускорением точки 
в данный момент времени 
и обозначается 
: 
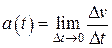, т.е. 
.
Но 
. Поэтому 
, т.е. 
.
Таким образом, вторая производная пути по времени есть величина ускорения прямолинейного движения, т.е.
.
Рассмотрим функцию двух переменных, заданную в явном виде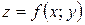 
. Её частные производные 
и 
являются также функциями двух переменных и 
. Следовательно, от них снова можно взять частные производные по и по :
,
,
Аналогично определяются частные производные третьего, четвертого и т.д. порядков. Так,
.
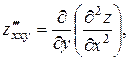
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например,
, 
, 
.
Пример. Найти частные производные второго порядка функции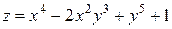 
.
Решение:
Так как 
и 
, то
,
,
,
.
Оказалось, что 
. Этот результат не случаен. Имеет место теорема.
Теорема 1. Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для 
имеем: 
.
