Прогнозируемые результаты обучения:
· Базовые понятия:
– способ задания функции,
– производная,
– порядок производной.
· Базовые операции:
– вычисление производной.
· Базовые методы:
– методы дифференциального исчисления.
При чтении лекции используется создание проблемных ситуаций, активизирующих познавательную деятельность студентов, с последующим составлением опорных конспектов.
Ориентация на развитие компетенций:
ОК-5 – способность к самоорганизации и самообразованию;
ПК-1 – способность к анализу и синтезу;
ПК – 8: способность использовать информационные средства и технологии при решении задач, возникающих в ходе профессиональной деятельности;
ОПК-4 – готовность сочетать теорию и практику для решения инженерных задач.
Производная неявно заданной функции
Если неявная функция одной переменной задана уравнением
,
а функция двух переменных – 
, то для нахождения производной функции одной переменной 
и частных производных функции двух переменных 
и 
нет необходимости разрешать уравнения относительно функций 
и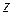 
.
Рассмотрим два способа дифференцирования неявно заданной функции.
Способ 1. Продифференцировать уравнение 
по 
, считая функцией от , а уравнение 
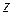отдельно по и по , считая функцией от и . Затем полученные выражения разрешить относительно (в случае функции одной переменной) и относительно , 
(в случае функции двух переменных).
Замечание. Производная неявно заданной функции является неявно заданной функцией.
Пример. Найти производные неявно заданных функций.
1. 
– неявно заданная функция одной переменной.
.
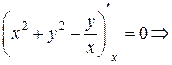
Выразим :
.
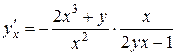
2. 
– неявно заданная функция двух переменных.
Найдем частные производные 
и . Для этого:
– продифференцируем уравнение по : 
, выразим : 
;
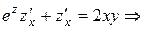
– продифференцируем уравнение по : 
, выразим : 
.
Таким образом, 
и 
.
Способ 2.
Пусть дана неявно заданная функция одной переменной.
1) Подставим в уравнение функцию 
: 
.Продифференцируем полученное уравнение по независимой переменной как сложную функцию двух переменных, используя формулу (2.3.11) (см. п. 2.3.4).
, тогда 
, 
.
Таким образом, 
.
2) Пусть дана неявно заданная функция двух переменных.
Продифференцируем 
по и по как сложную функцию, используя формулу (2.3.11) (см. п. 2.3.4).
, 
.
Таким образом, 
, 
.
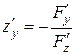Примеры. Найти производные неявно заданных функций.
1. 
– неявно заданная функция одной переменой.
, здесь 
.
, 
.
2. 
– неявно заданная функция двух переменных.
, здесь 
.
, 
, 
.
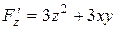Тогда 
, 
,
т.е. 
, 
.
Оба рассмотренных способа применяются и для вычисления частных производных неявно заданной функции 
независимых переменных вида
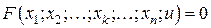, (3)
где 
.
Чтобы найти 
– частную производную такой функции по переменной 
, необходимо продифференцировать уравнение (3) по , считая 
функцией от переменных 
(способ 1), или воспользоваться формулой 
(способ 2).
