Рассмотрим функцию одной переменной 
, определенную на некотором интервале 
.
Проделаем следующие операции:
– аргументу 
дадим приращение 
, причем 
;
– найдем соответствующее приращение функции: 
;
– найдем «среднюю скорость» изменения функции на отрезке 
, равную 
;
– так как при 
значение «средней скорости» стремиться к значению скорости изменения функции в точке, то найдем последнюю как предел
.
Производная характеризует скорость изменения функции в данной точке.
Определение. Производной функции одной переменной в точке 
называется предел отношения приращения функции к приращению аргумента в этой точке, при стремлении к нулю приращения аргумента. Обозначается 
.
.
Пример. Найти производную функции 
.
Решение: Зададим приращение аргументу: 
.
Тогда 
.
.
Теперь, 
,
т.е. 
.
Ответ: 
.
Обобщая, можно сказать, что если функция описывает какой-либо физический процесс, то производная 
есть скорость протекания этого процесса. В этом состоит физический смысл производной.
В частности, если этот процесс – прямолинейное неравномерное движение, то скорость движения материальной точки в момент времени t есть производная от пути 
по времени t. В этом заключается механический смысл производной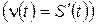 
.
В задаче про касательную к кривой был найден угловой коэффициент касательной 
, но 
.
Следовательно, производная 
в точке 
равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна . В этом заключается геометрический смысл производной.
Зная это, можно составить уравнение касательной и нормали (прямой, перпендикулярной касательной в точке касания) к графику функции.
Если 
– точка касания (см. рис.2.3.3) и 
, то 
.
Тогда, используя уравнение прямой проходящей через заданную точку в заданном направлении 
, можно записать:
– уравнение касательной: 
;
– уравнение норма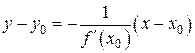ли: 
(если 
).
Теперь рассмотрим функцию двух переменных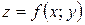 
, определенную на некоторой области 
.
Так как и 
– независимые переменные, то одна из них может изменяться, а другая сохранять свое значение.
Проделаем следующие операции:
– независимой переменной дадим приращение , сохраняя значение неизменным;
– найдем соответствующее приращение функции 
– частное приращение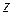 
по , т.е. 
;
– найдем среднюю скорость изменения значения функции в направлении координатной оси 
на интервале , равную 
;
– найдем скорость изменения функции в точке в направлении оси , перейдя в последнем равенстве к пределу при
.
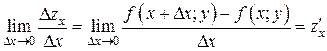Аналогично можно найти частное приращение функции по переменной : 
, и получить скорость изменения функции в точке в направлении оси 
:
.
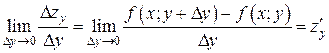Определение. Если существует предел отношения частного приращения функции в точке 
к соответствующему приращению независимой переменной при стремлении последнего к нулю, то он называется частной производной функции в точке по данной независимой переменной. Обозначается 
.
, 
.
Аналогично для функции 
– независимых переменных 
:
.
Таким образом, функция двух переменных имеет две частные производные, а функция переменных 
будет иметь частных производных.
Из определения частных производных следует, что частная производная находится в предположении, что изменяется только одна независимая переменная, а остальные остаются постоянными.
 |
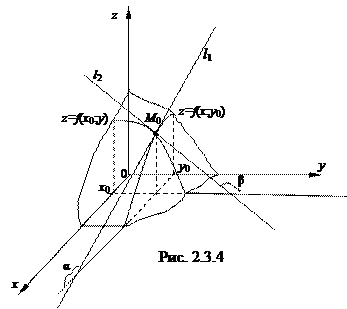Графиком функции
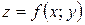является некоторая поверхность (см. рис. 2.3.4). График функции 
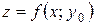есть линия пересечения этой поверхности с плоскостью 
. Исходя из геометрического смысла производной для функции одной переменной (см. выше) делаем вывод, что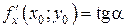 
, где 
– угол между осью и касательной 
проведенной к кривой 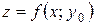в точке касания 
. Аналогично, 
, где 
– угол между осью и касательной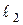 
проведенной к кривой 
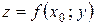в точке 
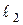. Это и есть геометрический смысл частных производных функции двух переменных.Прямые и определяют плоскость 
, которая называется касательной плоскостью к поверхности, являющейся графиком функции 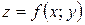в точке , значит, координаты всех точек прямых и 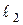удовлетворяют уравнению этой плоскости.
Используя геометрический смысл частных производных и уравнение плоскости, проходящей через точку : 
, можно составить уравнение плоскости .
Уравнение касательной плоскости:
. (2.3.6)
Прямая, проходящая через точку и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется нормалью к поверхности.
Используя условия перпендикулярности прямой и плоскости, легко получить каноническое уравнение нормали.
