При приближении к предельной точке, общей для нескольких бесконечно малых функций, скорость их стремления к нулю бывает различной. Сравнение таких бесконечно малых функций привело к понятию порядка малости.
Если 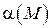 – бесконечно малая величина в окрестности точки
– бесконечно малая величина в окрестности точки 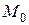 , т.е.
, т.е.  , то
, то  – бесконечно малая функция
– бесконечно малая функция  -го порядка малости.
-го порядка малости.
Чем выше порядок малости, тем быстрее переменная стремится к нулю.
Чтобы сравнить две бесконечно малые функции надо найти предел их отношения.
Пусть 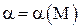 и
и  есть бесконечно малые функции при
есть бесконечно малые функции при  , т. е.
, т. е.  и
и  .
.
1. Если  , то при
, то при 
 быстрее, чем
быстрее, чем 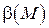 , поэтому
, поэтому 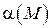 – бесконечно малая, более высокого порядка малости.
– бесконечно малая, более высокого порядка малости.
2. Если 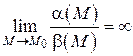 , то при
, то при 
 быстрее, чем
быстрее, чем 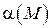 , поэтому
, поэтому 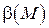 – бесконечно малая, более высокого порядка малости.
– бесконечно малая, более высокого порядка малости.
3. Если  , то
, то 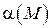 и
и 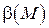 – бесконечно малые одного порядка малости.
– бесконечно малые одного порядка малости.
4. Если  не существует, то
не существует, то 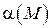 и
и 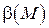 – несравнимые бесконечно малые.
– несравнимые бесконечно малые.
Отметим, что таковы же правила сравнения бесконечно малых функций при 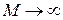 .
.
Примеры.
1. Сравнить порядок функций  и
и  при
при  .
.

 и
и  бесконечно малые функции одного порядка при
бесконечно малые функции одного порядка при  .
.
2. Сравнить порядок функций  и
и  при
при  .
.

 – бесконечно малая более высокого порядка.
– бесконечно малая более высокого порядка.
3. Можно ли сравнить функции  и
и  при
при  ?
?
Рассмотрим передел  .
.
Этот предел не существует при 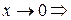 функции
функции  и
и 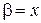 при
при  являются несравнимыми бесконечно малыми функциями.
являются несравнимыми бесконечно малыми функциями.
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые функции.
Определение. Бесконечно малые функции 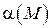 и
и 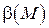 называются эквивалентными при
называются эквивалентными при  , если
, если  ;
;
это обозначается так:  .
.
Пример.  при
при  , так как
, так как  ;
;  при
при  , так как
, так как  .
.
Теорема 8. Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Доказательство:
Пусть  и
и  при
при  . Тогда
. Тогда
 , т.е.
, т.е.  . Ч. и т. д.
. Ч. и т. д.
Очевидно также, что  .
.
Теорема 9. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая их них.
Теорема 10 (обратная). Если разность бесконечно малых функций 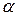 и
и  есть бесконечно малая более высокого порядка малости, чем
есть бесконечно малая более высокого порядка малости, чем  или
или  , то
, то 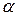 и
и  – эквивалентные бесконечно малые.
– эквивалентные бесконечно малые.
Терема 11. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Доказательство:Докажем теорему для двух функций. Пусть  ,
,  при
при  , причем
, причем  – бесконечно малая функция большего порядка малости, чем
– бесконечно малая функция большего порядка малости, чем  , т.е.
, т.е.  .
.
Тогда  при
при  .
.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.
Замена суммы бесконечно малых величин её главной частью называется отбрасыванием бесконечно малых высшего порядка.
Пример. Найти предел  .
.
Решение:Так как  , а
, а  (так как
(так как  – бесконечно малая функция более низкого порядка малости чем
– бесконечно малая функция более низкого порядка малости чем  ) при
) при  (см. теорему 11), то
(см. теорему 11), то  .
.
Для раскрытия неопределенностей вида 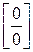 часто бывает полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций.
часто бывает полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций.
Известно, что  при
при  ,
,  при
при  . Приведем еще примеры эквивалентных бесконечно малых функций.
. Приведем еще примеры эквивалентных бесконечно малых функций.
Примеры.
1. Найдем 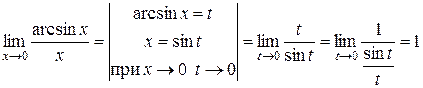 .
.
Следовательно,  при
при  .
.
2. Покажем, что  при
при  .
.
Т.е. докажем, что  . Действительно,
. Действительно,

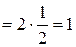 . Ч. и т. д.
. Ч. и т. д.
Значит,  при
при  .
.
Важнейшие эквивалентности приведены ниже:
при 
1. 
| 6. 
|
2. 
| 7. 
|
3. 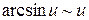
| 8. 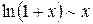
|
4. 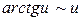
| 9. 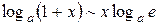
|
5. 
| 10.  в частности,
в частности, 
|
Примеры.
1. Найти  .
.
При 
 ,
,  , тогда
, тогда

2. Найти  .
.
При 
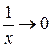 , тогда
, тогда 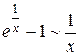 . Получаем
. Получаем  .
.
3. Найти 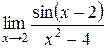 .
.
При 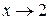
 , тогда
, тогда
 .
.
ЛЕКЦИЯ 2.3. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ. ОПРЕДЕЛЕНИЯ ПРОИЗВОДНОЙ И ЧАСТНЫХ ПРОИЗВОДНЫХ, ИХ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ, ТАБЛИЦА ПРОИЗВОДНЫХ
Прогнозируемые результаты обучения:
· Базовые понятия:
– приращение аргумента,
– приращение функции,
– производная,
– частная производная,
– касательная,
– скорость и ускорение движения.
· Базовые операции:
– вычисление производной,
– применение понятия производной.
При чтении лекции используется создание проблемных ситуаций, с элементами визуализации, активизирующих познавательную деятельность студентов.
Ориентация на развитие компетенций:
ОК-5 – способность к самоорганизации и самообразованию;
ПК-1 – способность к анализу и синтезу;
ПК – 8: способность использовать информационные средства и технологии при решении задач, возникающих в ходе профессиональной деятельности;
ОПК-4 – готовность сочетать теорию и практику для решения инженерных задач.
Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики и других наук, в особенности при изучении скорости разных процессов.






