Функция 
, где 
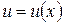– сложная функция с промежуточным аргументом 
и одной независимой переменой 
.
Теорема 1. Если функция 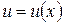имеет производную 
в точке , а функция имеет производную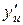 
в соответствующей точке 
, то сложная функция 
имеет производную 
в точке , которая находится по формуле
.
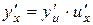Доказательство: По условию теоремы
1. 
, отсюда, на основании теоремы 7 п. 2.2.3
или 
, (2.3.7)
где 
при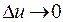 
.
2. 
, поэтому 
, где 
при 
.
Подставляя 
в (2.3.7), получим: 
, т.е. 
, 
.
В последнем равенстве, перейдя к пределу при , получаем
.
Таким образом, 
. Ч. и т. д.
Пример. 
: 
, где 
,
.
Замечание. Если промежуточных аргументов несколько теорема 1 остается в силе. Так, если , 
и 
, то
.
Пример.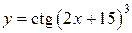 
: 
, 
и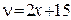 
.
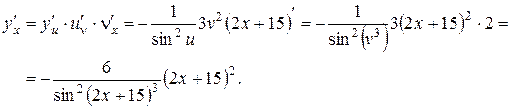
Рассмотрим функцию двух переменных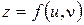 
, где 
, 
. Тогда 
– сложная функция независимых переменных и 
.
Теорема 2. Если 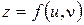– дифференцируемая функция и , – дифференцируемые функции независимых переменных и , то производная сложной функции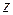 
по каждой независимой переменной и равна сумме произведений частных производных этой функции по ее промежуточным переменным и 
на их производные по соответствующей независимой переменной и .
, (2.3.8)
. (2.3.9)
Пример. Дана функция 
, где 
и 
. Найти 
, 
.
Решение: Найдем , используя формулу (2.3.8).
Предполагая, что – свободная переменная, а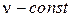 
, найдем 
: 
.
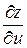Предполагая, что – свободная переменная, а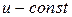 
, найдем 
: 
.
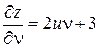Теперь найдем 
и 
: 
, 
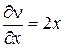, тогда 
.
Найдем , используя формулу (2.3.9). 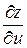и известны. Теперь найдем 
и 
: 
, 
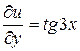, тогда 
.
Ответ: 
, 
.
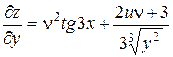Теорема 3. Если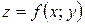 
дифференцируемая функция и 
, 
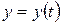дифференцируемые функции независимой переменной 
, то производная сложной функции 
вычисляется по формуле
. (2.3.10)
Следствие. Если 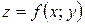дифференцируемая функция и 
– дифференцируемая функция независимой переменной , то производная сложной функции 
вычисляется по формуле
. (2.3.11)
Производная обратной функции
Пусть 
и 
– взаимно обратные функции.
Теорема 4. Если функция строго монотонна на интервале 
и имеет производную 
в произвольной точке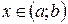 
, то обратная ей функция также имеет производную 
в соответствующей точке, которая вычисляется по формуле
или 
(2.3.8)
Доказательство: Рассмотрим обратную функцию . Дадим аргументу приращение 
. Ему соответствует приращение 
обратной функции. Так как – строго монотонная, то 
. И поэтому можно записать 
.
В силу непрерывности обратной функции 
при 
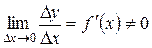(по условию), тогда
.
Значит . Ч. и т.д.
Пример. Найти производные обратнотригонометрических функций и показательной функции.
1. 
, 
: 
,
.
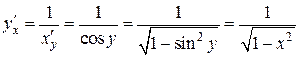2. 
, 
: 
,
.
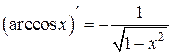3. 
, 
: 
,
.
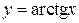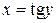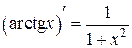4. 
, 
: 
,
.
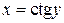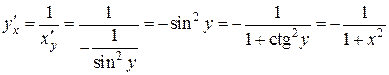5. 
, 
: 
,
.
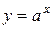6. 
, 
: 
,
.
Таблица производных
На практике чаще всего приходится находить производные от сложных функций, поэтому в приведенной ниже таблице формул дифференцирования аргумент заменен на промежуточный аргумент .
1. 
| 9.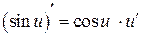 
|
2. 
| 10. 
|
3. 
| 11. 
|
4. 
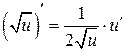
| 12. 
|
5. 
| 13. 
|
6. 
| 14. 
|
7. 
| 15. 
|
8. 
| 16.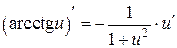 
|
