Используя данные о длине дуги контакта, рассчитываем среднее

значение толщины отделяемого элемента:

. и (3.14)

Si Н Sj. Н со

^{6Р 1}СВ ~(*1 ^{+ (ой}>^о

Рассмотрим некоторые методы более упрощенного определения длины дуги контакта фрезы с заготовкой (АЕ, С Б и т.д). Пред­положим, что фигура АЗЕ (см. рис. 3.4) представляет собой треу­гольник, в котором угол АЗЕ ^в 180 - Y₀. Тогда согласно рис. 3.4 имеем:

1 «"\ =^(АЗ)^г+ (ЗЕ)2+ ZA3-3EcosCieo°-V_e)' =

■■fwaY+ (

5%. %

И' " ^f^-V

-v„^7|:

Н* - щ±«*. ■ ^(ЗЛ5)

Г

С допущениями можно также принять, что траектории А Е, С Б и т.д. совпадают с дугами окружностей (рис. 3.5). В результате

Рассмотрим еще один способ упрощенного определения средней толщины отделяемого элемента срезаемого слоя. Сравним сечения, проведенные через точки К и С отделяемого элемента, перпендику­лярно к вектору скорости главного движения (см. рис. 3.5)."Если условно принять, что фигуры ЗТС и ИКБ представляют собой треу­гольники, в которых угол ТСЗ = 90°-V₀, а угол ИКБ = 90-Ч', го соотношения сторон в них удовлетворяют следующим зависимостям:

(3.16)

^TC=auv,c^=aVc ^{= s}t^si*^Vc'

По аналогии с (3.16) для любой точки X, взятой на дуге кон­такта фрезы с заготовкой, имеем:

(3.17)

a^^S^sih^,

где у — угол контакта X

При Y_x=%/E = V_cp получаем

(3.18)

Sep* ^a4'₀/2=^ac_P=4^si^^/2-)

Рис. 3.5. Упрощенная схема контакта цилиндрической фрезы с заготовкой изделия

Выразим значение угла yjl через геометрические параметры заготовки. Известно, что

Цт./г)=У

1 - COS То

(3.19)

Значение cos V₀ найдем из треугольника ОМЗ (см. рис. 3.4):
cosV^I- 2.H/2R=1- H/R, (3.20)

где R - радиу с фре зы. _____,

Тогда StH^=-^T,aa_cpS5tjl. (3.21)

После подстановки (3.16), (3.17) и (3.21) в уравнения (3.6) зависимости для расчета площадей сечений отделяемых элементов срезаемого слоя при фрезеровании цилиндрическими фрезами с прямы­ми зубьями принимают следующий вид:

 

f

гемг)"

^c4«=^evV*^nVa_!!

■«■

U,Up)=eVacp£eVbz

В чн

(3.22)

RY₀ '

Б. Обработка цилиндрическими фрезами с винтовыми зубьями

Режущие кромки на цилиндрических фрезах с винтовыми зубьями (рис. 3.6) расположены наклонно по отношению к образующей фрезы (на виде сверху (рис. 3.6) поверхность контакта показана в разверт­ке). Взятые на них точки имеют различные углы контакта с заготов­кой изделия. Так, например, для точек К и К одной из режущих

Рис. 3.6. Форма контакта винтового зуба цилиндрической фрезы с отделяемым элементом срезаемого слоя

Qy₂= QzK2

 

If			% 1			*Ч	Кг
	/ /		1 /
	/•			/щ	г1**		СП	1
	/	/			№<£у	CJi	У
/	/__	/		ш_		1	'
	Щ %'"		a», h К
					P*S

кромок углами контакта являются соответственно углы у, ц/. Об­разующаяся при этом площадка А К. К, А. представляет собой пят­но контакта передней поверхности режущего зуба фрезы (имеющего J * О) с отделяемым элементом срезаемого слоя. Толщина этой площадки при переходе от точки К. к точке К изменяется от а до а₄,₂. Для определения ее площади +_1К воспользуемся криволинейным интегралом

где 6^ - длина рабочей части режущей кромки винтового зуба фрезы; 1ы ^— мгновенное значение толщины пятна контакта зуба фрезы с отделяемым элементом срезаемого слоя; dS — длина элементарно­го участка режущей кромки винтового зуба фрезы.

Уравнение винтовой линии (режущей кромки) в системе коорди­
нат имеет вид: I-

Л = Я cos «у,

< 9=Rsifv_% ^(3,24)

г = ^у,

."де R - радиус

эезы; о - параметр винтовой линии. Если развернуть винтовую линию режущей кромки зуба на плос— сть, то получим:

Й/йЗГИ s ctq СО,

где к - шаг винтовой линии. Югсюда h/азг= Rctaco и ц,= R cto oj.

Определим величину as:

(3.25)

De^X^eia^dZ11.

Из (3.24) имеем:

dX = - Rstnifdif, - dil = ft cosq/oLtp,

dZ = Rctjj codcp.

После подстановки значений dX, d. У,dZ в (3.25) получим:

(3.26)

ds=Ry1-ct^ a) d«c = Rdc(//svHta?.

Так как 0.^= S^StH,^,

Rd¥, Sinu)

V****

i%

C0Stpx

SiKO)

SiHUJ

(cos^-cosa/j). (3.27)

%

 

При со "О и <р. ** <р, фреза с винтовыми зубьями превращается во фрезу с прямыми зубьями. На этой же основе при ьо •* О и у — " "Kj ^т %, формула (3.27) должна выражать значение площади сече— чения элемента, отделяемого зубом прямозубой фрезы (пятна контакта этого зуба, имеющего передний угол, равный нулю, и отделяемым элементом), и на основании (3.22) J_ZCmax, = 6_v S„ Sin.^ • Однако при подстановке со «О, % = Ц>_г ^ж <fc, в (3.27) получаем несколько иное выражение:

f / *'*' (3.28)

Для определения предельного значения формулы (3.27) при со-» О установим величину ^_гк Ссо-* 0) '

Представим (3.27) в следующем виде:

г *х R Г*. _, ⁽³'²⁹⁾

%

(3.30) (3.31)

Анализ геометрических параметров фрез с винтовыми зубьями (см. рис. 3.6) показывает, что

где В - ширина фрезеруемой площадки, откуда

Ч1_гк B/R tgco+ ч»,

Vr

Тогда

(3.32)

s R. Г
•f - & S \ stH (ф + иЛсссу.

^J*.K sin со J ^VY1 ^T^ ^T

По правилу Лопиталя для определения + _гк ^_ш^. ₀» нужно найти
производные от числителя и знаменателя и определить предел их от­
ношения: B_t

R f^R

■f „=Um» ^Sg I stn(ty+ty)dty =

J*KC«U*0) "^mco-»0 siHo, J ^VYi ^T' ^T

= tim

(3.33)

s_bsin (ч/₁₊ -^tgw)B

tt3-^0

cos^s со

_ Bs^inCc^+ltg 0°) zkcco=0)~ C0S3 o°

t

s_zsvh ^.

Так как при обработке фрезами с прямыми зубьями Б = 6_V, то по­ученное выражение (3.33) при Ч/,, ^м Щ₀ полностью совпадает с уста— овленной на основе (3.22) зависимостью ■f.,_|tta3t^=6_vs_!t siK (f«

Таким образом, нами доказано, что формула (3.27), служащая
ля определения площади пятна контакта винтового зуба фрезы с от­
деляемым элементом, справедлива также для фрез с прямыми зубья—
и.
Анализ формулы (3.27) показывает, что площадь пятна контакта
-уба фрезы с отделяемым элементом изменяется в процессе резания,
то происходит потому, что при повороте зуба фрезы изменяются
начения углов контакта V и ср и ширины пятна контакта в, (см.
.не. 3.6). В процессе резания в контакте с заготовкой, как прави­
ло, находятся одновременно не один, а несколько режущих зубьев.
Поэ тому остановим наше внимание на определении общей площади
пятен контакта всех одновременно участвующих в процессе фрезеро­
вания зубьев. Обозначим число зубьев через z'. Тогда зависимость
для определения суммарной площади пяген контакта будет иметь вид:
z¹ Z¹ ~ *'

(3,34)

^"ff.K-^^VUSf^^»'

где a _к - мгновенное среднее значение толщины площадки контакта ингового зуба со срезаемым слоем (рис. 3.6).

Обозначим через F, последнюю часть выражения (3.34):

X'

Определим величину F_f для случая, когда z " 3 (рис. 3.6). Примем дополнительное условие. Рассмотрим случай, когда В = К t ₀, где

j t - осевой шаг между зубьями фрезы. 2tQ, Схема расположения режу—

В - ширина фрезерования (рис. 3.6); К - любое целое число: 1, 2,3,.

Определим F. для случая В щих кромок, характерная для э того случая, приведена на рис. 3.6. Из построения имеем: % *= Ч/»'.'" Ц>_г и ЦТ¹'* О, У,» О. Тогда F, = = cos0°-cos4''+ cos0° - cos q£ + cos у"- cos ч£' При условии, что V I"⁼ fz ' получим:

F, = Z- 2coscp₀= £(1-cos ц>₀),

F₁₌^- (1- cos ij/₀) = const.

Подставив полученное значение F, в (3.34), имеем:

(3.35)

F =-------- -г- (.1- cos»).= const.

сам sinco t. V

 

Анализ выражения (3.35) показывает, что при принятых условиях (В = К t₀) суммарная площадь пятен контакта всех одновременно участвующих в рабоге винтовых зубьев фрезы, несмотря на постоян­ное их обновление в процессе фрезерования (вход одних и выход дру­гих), будет оставаться постоянной величиной. Фрезерование, при ко­тором F_E„_M⁼ Canst» получило название равномерного.

Параметры Н и В для случая фрезерования цилиндрическими фре­зами с винтовыми зубьями имеют те же значения, что и при обработ­ке фрезами с прямыми эубьями. В. Торцевое фрезерование

Установление параметров сечений элементов срезаемого слоя, от­деляемых при фрезеровании торцевой фрезой (рис. 3.7), упрощается,

в торцевую. Поэтому сечения отделяемых элементов срезаемого слоя при обработке торцевой фрезой по форме аналогичны тем, которые имеют место при обработке цилиндрической фрезой. Для примера пред­лагается сравнить рис. 3.4 и рис. 3.7.

3.2.4, Протягивание

Форма сечения элемента срезаемого слоя, удаляемого одной режу­щей кромкой при протягивании, зависит от последовательности вреза­ния зубьев протяжки в заготовку и размеров каждой режущей кром­ки, т.е. от условий, определяющих схему резания.

При протягивании различают следующие схемы резания: профильную, генераторную, прогрессивную (рис. 3.8). При профильной схеме реза-

 

I,m

Рис. 3.7. Форма сечений отделяемых элементов срезаемого слоя при обработке торцевыми фрезами

так как цилиндрическая фреза при ее повороте на 90 превращается

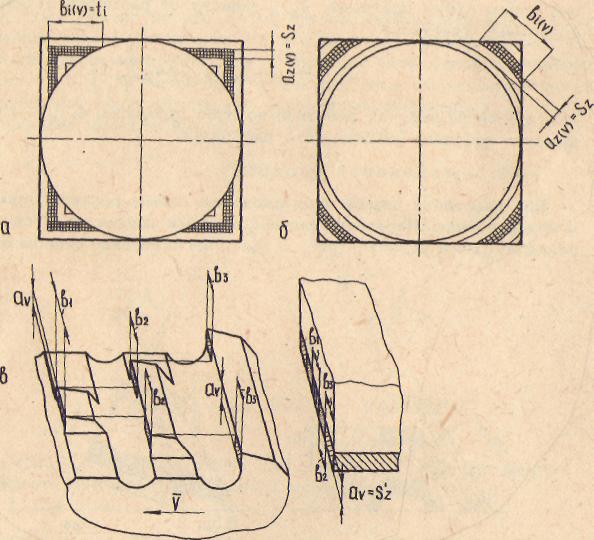
Рис. 3. 8. Форма сечений отделяемых элементов срезаемого слоя при протягивании: а-профильная схема резания; б - генераторная схема ре­зания; в - прогрессивная схема резания

 

ния (рис. 3.8,а) каждый зуб протяжки по форме совпадает с профи­лем обрабатываемой поверхности. При генераторной схеме (рис.3.8, б) зубья протяжки по форме не совпадают с профилем обрабатывае­мой поверхности, но последовательное участие их в процессе удале­ния срезаемого слоя обеспечивает образование (генерирование) за­данного профиля детали.

Прогрессивная схема резания (рис. 3.8,в) от профильной и гене­раторной отличается тем, что толщина элементов, отделяемых в этом случае каждым зубом протяжки (или ее части - секции), равна пол­ной толщине принятого под срезание слоя. Режущие кромки различ­ных зубьев протяжек имеют вид ломаных или прерывистых линий, длина которых постепенно изменяется при переходе от одного зуба к другому. Поэтому общая площадь слоя, удаляемого при протягива­нии одним зубом протяжки f, зависит от размеров отдельных срезаемых участков:

и. к

J*^{= a}xcv) 2- e_icv)=Sji2 t.,

где К — число рабочих участков на зубе протяжки; 6;_(v. — ширина каждого рабочего участка (см. рис. 3.8).

3.2.5. Нарезание резьбы

При нарезании резьбы возможны две схемы резания: профильная и генераторная. Нарезание резьбы резцами осуществляется по про­фильной схеме резания (рис. 3.9,а). При нарезании резьбы метчиком

 

(3.36) — число режу— (3.37)

или плашкой образование выемок резьбы осуществляется чаще всего по генераторной схеме резания (рис. 3.9,6). В этом случае каждая впадина резьбы образуется последовательным вхождением в нее всех режущих кромок, имеющихся, на заборной части метчика. Определим их количество:

ZPtt.

где fc. - число режущих кромок на заборной части; Z» щих кромок на одном зубе; и. - число канавок. Так как

где t_ - длина заборной части; М - шаг резьбы, то

(3.38)

Р/м)к.

{9 + Щ)МЧ

Рис. 3.10. Расчетная схема определения толщины срезаемого элемента при нарезании резьбы метчиком

Для приведенного на рис. 3.9,6 случая нарезания резьбы (по ге­нераторной схеме) характерно го, что ширина сечений отделяемых элементов срезаемого слоя ^цу> является переменной величиной. Толщина же Ъщ^ остается постоянной для всех отделяемых элемен­тов. Установим зависимость для определения величины a_acV) для слу­чая нарезания метрической резьбы (рис. 3.10).

 

D S*, С „Угы

А 5

Рис. 3.9. Форма сечений отделяемых элементов срезаемого слоя при нарезании метрической резьбы: а — профильная схема резания; б — генераторная схема резания

Общая толщина слоя, удаляемого поэлементно при постепенном участии всех находящихся на заборной части метчика лезвий, равна наибольшему размеру А впадины резьбы. Величину этого размера определим из схемы, приведенной на рис. 3.10:

А= Hcosipt (Pt Hto |)sitiif>. (3.39)

 

При известном значении общего количества режущих кромок на за­борной части метчика X., принимающих участие в поэлементном уда­лении срезаемого слоя, толщину одного отделяемого элемента a.^_cv-. определим по зависимости

А (3.40)

^а«\0 = г₃'

После замены А и г, в соответствии с (3.38) и (3.39) получим? [Hcosqn- (E+Htaf)siH4>] м

<4cv)----------------- 1^ ^(3,41)

Подобно тому как это делалось ранее для других видов обработки резанием, определим значения двух других параметров сечения отде­ляемого элемента (в ■, t) при нарезании резьбы метчиком. За направление подачи в этом случае может быть принято направление, совпадающее с вектором скорости V,.. или перпендикулярное к нему (см. рис. 3.9). Поэтому за параметр сечения, определяющий рассто­яние между двумя соседними следами поверхностей резания в направ­лении вектора подачи, может быть принят размер БС •* S_XI или ВС ** "* Sj. Тогда перпендикулярно к S,и S убудут расположены взаимо­связанные с ними размеры t₍ a t (см, рис. 3.9). Размер S_x) явля­ется частью вектора скорости перемещения метчика вдоль оси изде­лия V.jjj. Раскладывая этот вектор не составляющие, имеем:

V_£Xl = HM _{= t}vS₀ = x₃^DC = nz₃S_x1; S_x1=-^~'

где М — шаг резьбы, мм; S₀ - перемещение метчика вдоль оси, мм/об; к — частота вращения метчика, об/мин; 2«- число режущих кромок на заборной части метчика.

Величину S_ найдем из треугольника UBC (см. рис. 3.9):

 

Значение площади сечения элемента слоя, отделяемого одним зу­бом метчика, зависит от толщины сечения и суммарной длины участ­ков режущих лезвий зуба метчика, принимающих' участие в продессе резания:

It

iziCIW" ^aUV)2p0UV)> (3.42)

3.2.6, Зуб ообработка (обработка долбяком и червячной фрезой)

При этих видах зубообработки постепенное вхождение зубьев режу­щего инструмента в выемку зубчатого колеса сопровождается посто­янным изменением формы сечения отделяемых элементов. Их площади (заштрихованные участки) можно охарактеризовать с помощью ряда мгновенных значений толщины отделяемых элементов срезаемого слоя a _t и ширины в., (рис. 3.11).

 

где и. - число рабочих участков (режущих кромок) на зубе метчика;

*iCV)~ Длина каждой режущей кромки, принимающей участие в про­цессе резания (см. рис. 3,9).

Рис. 3.11. Формы сечений отделяемых элементов срезаемого слоя при обработке зубчатых колес: а - долбяками; б- червячными фрезами при вершинонагруженной схеме резания

 

Зуборезные инструменты могут гак же, как и другие инструменты, работать по прогрессивной схеме резания. На рис. 3.11,6 приведена схема образования отделяемых элементов срезаемого слоя при обра­ботке червячной фрезой, работающей по прогрессивной схеме резания. Такая фреза отличается от стандартной тем, что ее зубья с нечетны­ми номерами (1,3,5,7) вдоль витка выполнены заниженными по тол­щине, а четные (2,4,6,8) *. заниженными по вершине. Такие фрезы получили название фрез с вершинонагруженной схемой резания.

ГЛАВА 4

ВХОДНЫЕ ХАРАКТЕРИСТИКИ ПРОЦЕССА РЕЗАНИЯ

Теория резания базируется на основных положениях механики и физики. Взаимодействие режущего инструмента и срезаемого слоя, геометрия резания служат основными предпосылками создания исход­ных моделей

4.1. ИСХОДНЫЕ МОДЕЛИ ЗОНЫ РЕЗАНИЯ

Растяжение или сжатие металлических образцов⁴ сопровождается появлением максимальных ■ касательных напряжений в поверхностях сдвига, расположенных под углом, близким к 45. Когда напряжения превышают предел текучести материала на сдвиг, происходит переме­щение элементов образца вдоль поверхностей сдвига. Процесс резания представляет собой совокупность процессов динамического сжатия и установившегося сдвига локальных участков срезаемого слоя.

4.1.1. Простейшие схемы зоны ортогонального резания

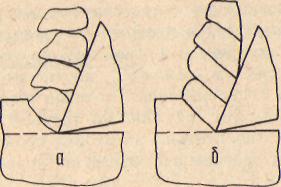
Зону ортогонального (прямоугольного) резания образуют (рис.4.1): режущий клин 1, отделяемый объем 2 срезаемого слоя, постепенно переходящий в стружку, и обработанная поверхность изделия 3. Дей­ствующий при этом механизм отделения и перевода в стружку объема срезаемого слоя заключается в последовательных сдвигах его локаль­ных участков Ж¹, Ж вдоль поверхности максимальных касательных напряжений (обозначим след поверхности через ОС), расположенной под углом ji, к направлению перемещения инструмента.

Начальный этап отделения объема срезаемого слоя заключается в том, что инструмент из исходного положения перемещается силой F

Рис. 4.1. Модель зоны ортогонального резания при положитель­ном (а) и отрицательном (б) переднем угле у

в направлении ее действия и, преодолевая упругую деформацию метал­ла, внедряется в заготовку. На втором этапе по мере внедрения инст­румента в заготовку происходит нарастание сопротивления деформиро­ванию. В тог момент, когда действующая в поверхности максималь­ных касательных напряжений ОС (см. рис. 4.1) (назовем ее условной плоскостью сдвига^ составляющая силы давления F „. достигает вели­чины, "достаточной для преодоления сопротивления металла сдвигу,-происходит образование первого элемента стружки. На третьем этапе по мере перемещения инструмента относительно заготовки происходят последовательные сдвиги элементов срезаемого объема по условным плоскостям сдвига, параллельным О С.

Определим значение угла jv, который характеризует положение условной плоскости сдвига. Опустим из точки С перпендикуляры С Б и С б. (рис. 4.1). Тогда

_рс^ СБС Б, (4.1)

 

Анализируя выражение (4.2), приходим к выводу, что при a» a,

(JJV (l+StHJ-J,, В круглых скобках в формулах (4.1)-(4.3) знак "минус относит­ся к схеме рис. 4.1,а, а "плюс" - к рис. 4.1,6. При V = О tan,»-*. И.4) В результате сдвигов наружная поверхность стружки получается пилообразной. На поверхности, контактирующей с передней поверхнос­тью инструмента, неровности обычно сглаживаются за счет трения. Образующаяся стружка по длине может быть разделена на элемен­ты рядом линий, которые являются следами поверхностей сдвига. Она может быть и сплошной, и в виде ленты (рис. 4.2). В зависимости от расположения элементов различают следующие виды стружки: эле­ментная (рис. 4.2,а), суставчатая (рис. 4.2,6), сливная (рис. 4.2,в) и надлома (рис. 4.2,г). Первые три вида образуются при резании пла­стичных материалов. По мере увеличения твердости и прочности обра­батываемых материалов стружка из сливной переходит в суставчатую

или элементную. При обработке хрупких материалов образуются толь­ко два вида стружек: элементная и надлома. Стружку надлома часто называют стружкой отрыва, гак как ее-образование связано не со сдви­гом, а с отрывом кусочков (элементов) отделяемого объема. Эта

A.

C6 = a; СБ,-.., откуда выражение для определения утла вид:

:$JV

a/сц cos у

cosy

Рис. 4.2. Виды стружек

A/tysiHj

 

(4.3)

ft, (угла сдвига) получает (4.2)

стружка, как и элементная, состоит из отдельных, не связанных друг с другом кусочков различной формы и размеров. Поверхности от­деления кусочков стружки надлома могут располагаться ниже по­верхности резания. В результате обработанная поверхность оказы­вается покрытой вырывами, углублениями.

Рассмотренная модель зоны резания значительно упрощена (идеа­лизирована). В этой модели основу механизма с тру жко образования составляет принцип геометрического моделирования. Более сложным является динамическое моделирование, которое базируется на теоре­тических положениях механики сплошных сред, теории пластичности и упругости твердых тел и других физико—механических закономер­ностях.

Приложение теории пластичности к процессу резания показывает, что модель с одной условной плоскостью сдвига применима для прос­тых видов пластических деформаций, таких как растяжение металли­ческого образца, сжатие при отсутствии внешнего трения..Отметим, что выводы и положения теории пластичности к резанию металлов можно применять с некоторым приближением. Например, в теории пластичности не учитываются гетерогенность и анизотропность обра­батываемого материала, изменение его физических свойств и механи­ческих характеристик под влиянием высоких скоростей. При резании металл в процессе сгпужкообразования находится в сложном напря­женном состоянии. В зоне пластической деформации будет располагать -ся веер поверхностей сдвига, выходящих из одной точки.

Усовершенствование модели зоны резания путем дополнения ее фи­зическими (металловедческими) данными на атомном уровне привело к моделированию процесса резания с использованием дислокационных представлений физики твердого тела [105]. Однако реализация мето­да дислокаций требует постановки сложных экспериментальных иссле­дований. Отметим, что часто предпринимаемые с целью усовершенст­вования упрощенной модели зоны резания исследования приводят лишь к незначительному уточнению получаемых результатов.

На начальном этапе изучения процесса резания используем модель с одной условной плоскостью сдвига.

4.1.2. Модель пластической деформации зерен (металла в срезаемом слое

Многочисленные исследования срезов стружки под микроскопом по­казывают, что структура металла стружки отличается от структуры металла основной части заготовки. Зерна основной части металла имеют в некотором приближении шаровидную форму. Стружка же сос­тоит из зерен, имеющих вытянутую, эллипсоидную форму (т.е. из пла­стически сдеформированных зерен). Зерна в стружке располагаются

 

 

гак, чгс большая их ось составляет угол ft с направлением пере­мещения инструмента (рис. 4.3).

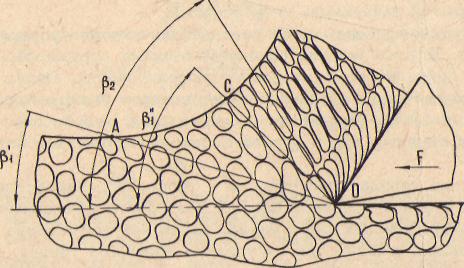
Рис. 4.3. Схема текстуры металла в зоне стружкообразования

Наблюдаемая в стружке упорядоченность расположения зерен полу­чила название текстуры стружки. Она заканчивается на границе с не­которой переходной зоной ДОС, ограниченной углами jj^ и р". С одной стороны от переходной зоны находятся свободные, недеформи-рованные зерна металла заготовки, а с другой — текстура пластичес­ки сдеформированных, имеющих эллипсоидную форму зерен стружки.

Переходная зона ДОС представляет собой зону, в которой осу­ществляется пластическая деформация зерен (зону пластической дефор­мации). Зерно металла, постоянно проходя эту зону и ропадая в струж­ку становится пластически сдеформированным. Размеры переходной зоны зависят от условий обработки. При больших скоростях резания границы переходной зоны сужаются настолько, что практически плас­тическая деформация зерен осуществляется почти вдоль! одной плос­кости сдвига, например ОС, как это было показано ранее на приме­ре простейшей модели зоны ортогонального резания (см. рис. 4.1).

Рассмотрим механизм пластического деформирования [отдельного зерна металла в процессе резания. Воспользуемся для этого моделью зоны ортогонального резания с одной условной плоскостью сдвига. Пусть на зерно металла (в виде шара, вписанного в куб;) действует сила, вызывающая определенную сдвиговую деформацию (рис. 4.4). Сдвиг происходит в направлении действия силы F. Зерна металла при этом изменяет свою форму — верхняя грань куба 1—2 смещается на

Рис. 4.4. Схема деформации при сдвиге

некоторую величину д S и занимает положение 1-2', основание зерна ^-4 остается неподвижным. Не изменяется и расстояние между слоя-и ДИ. Количественной характеристикой степени такой сдвиговой де-прмации является величина относительного сдвига е, равная отноше­нию величины смещения д S к расстоянию между слоями металла дЬ:

£= дб/дк =tc| В, (4.5)

де 0 - угол поворота граней 1-4 и 2-3.

Перенесем условно такое зерно в срезаемый слой. Рассмотрим ге-метрическую модель зоны резания, представленную на рис. 4.5.

Рис. 4.5. Модель деформации зерна металла в процессе сдвига

Здесь 00-) С₁ С - элемент срезаемого слоя, который переводится в 1сг.ружку при перемещении резца из положения I в положение П. При 1©гом точка 0 переходит в точку 0,, а линия О С параллелограмма

 

12 9

CfCOOi перемещается (сдвигается) параллельно О, С| и занимает по­ложение Б С,. Одновременно точка 0 переходит и в точку 6. а точ­ка С - в точку С,. В результате элемент 00^ С₁С оказывается рас­положенным в стружке. Выделим в нем элементарное зерно металла, для чего из точек 0. и С проведем две линии, перпендикулярные к

ОС. Пусть шар, вписанный в квадрат CCoO. 0», представляет собой искомое зерно металла. При сдвиге слоя ОИ^ЦС" сдвиговую деформацию получит и зерно СС«0₁ 0,. Оно займет положение OjC-CjO.- В резуль­тате сдвига С_г0» = (ГОв» квадрат CCjOjQ, перейдет в параллелограмм

(LCiCjCL • Зерно вместо шаровидной приобретает эллипсоидную фор­му, располагаясь своей большей осью под углом Л. к направлению пе­ремещения инструмента, что характерно для текстуры пластически с деформированных зерен.

Определим величину относительного сдвига зерна металла при его деформации в срезаемом слоя. Из рис. 4.5 имеем:

aS _ СС_г _ ОБ,. 00г, ОгБ ⁽⁴'-⁶⁾

^£= л К ⁼ 0,0,," 0,0_г~ 0,02 ⁺ 0,0;, '

После преобразования выражения (4.6) получим:
или. р -.

е= cosy/^vn^cosc^-yij-

Математический анализ выражения (4.7) затруднителен. Поэтому обратимся к рис, 4.5, из которого находим, что при увеличении пе­реднего угла Y размер О Б — Л S уменьшается, так как точка Б при­ближается к точке 0. Увеличение же угла, JJ,. ведет к увеличению размеров й S и & U, причем й Ц будет возрастать в большей степе­ни. В результате приходим к выводу, что с увеличением V и JJ ве­личина относительного сдвига будет уменьшаться.

Определим условия, при которых величина относительного сдвига имеет минимальное значение. В этом случае dt/c(.ft,= 0. Продифферен­цируем это выражение:

<k₌__L_ ₊____!___ ₌о

dji, SlK*/», C08*(J,-jp
Получим J

h^skS°*it ⁽⁴-⁸⁾

При У ~ О |>1 ⁼ 45, а наименьшее значение относительного сдвига равно 2.

Пользуясь рис. 4.5, нетрудно установить соотношение между уг­лами в, и jb_£:

ct3(jyjV=(e+-\[I*+T)/u. (4.9)

Следует отметить, что зерна стружки, расположенные в погранич­ном с передней поверхностью инструмента слое, получают значитель­ную дополнительную деформацию в процессе их перемещения вдоль пе­редней поверхности и оказываются в конечном итоге сильно вытяну­тыми вдоль передней поверхности.Величина деформации в этой зоне обычно в несколько раз превышает деформацию в плоскости сдвига.Ее можно представить,рассмотрев изменение формы элементарного куба в пограничном слое,толщина которого равна,например, 0,075 мм, а длина площадки контакта 1,5 мм. Пусть в исходном состоянии куб с размером грани 0,075 мм расположен на передней поверхности у ре­жущей кромки. Когда его верхняя грань сместится на расстояние 1,5 мм (в положение, в котором стружка отрывается от передней по­верхности) относительный сдвиг будет равен 18, что значительно больше (в 4—5 раз), чем в плоскости сдвига. Однако фактически эта величина может быть значительно больше, так как в условиях пласти­ческого торможения основание куба может оставаться прикрепленным к поверхности инструмента неограниченно долго, в то время как верх­няя его грань будет иметь возможность длительного пластического течения относительно нижней.

■ 4.1.3. Схемы сил и скоростей в зоне резания

По аналогии с внедрением клина в неподвижное тело (рис. 4.6,а) в зоне резания усилие со стороны режущего клина на заготовку пере­дается его рабочими поверхностями. Согласно рис. 4.6,6 имеем:

где Я - равнодействующая внешних сил.

Силы сопротивления резанию, действующие на режущий клин со сто­роны срезаемого слоя и заготовки изделия, концентрируются на пе­редней и главной задней поверхностях режущего инструмента. Перед­няя поверхность испытывает на себе действие двух сил: силы нормаль­ного давления стружки N. и силы F,.

Давление со стороны заготовки на заднюю поверхность передает­ся соответственно через силы N. и F,. Условно примем, что сила N нормальна, а сила F. касательна к поверхности резания. Направление сил N^. Fj, F«, No зависит от того, какое из тел в процессе реза­ния рассматривается неподвижным - заготовка (рис. 4.6,г) или ре­жущий инструмент (рис. 4.6,в). Примем условно, что силы сопротив­ления резания приложены к вершине режущего клина в системе коор­динат X0Z (рис. 4.6,в,г).

 

t^W:

(4.14)

N,cosy +F,stnj»+ Fi

Угол со получил название угла действия, он характеризует соот­ношение сил F' и F,.

г иг) Ы

Проведем преобразование исходной схемы сил зоны резания. Спро­ектируем вектор fv на два новых направления, одно из которых сов­падает с условной плоскостью сдвига, а другое перпендикулярно к ней (рис. 4.6,г). В итоге получим:

*с=кг

f;

f;3+

!сЭ

(4.15) (4.16)

-Щ

: i сгъ

1С2).

COS О)

иг>

iu-ufST

= F

+ F

= F,

 

(4.18)

R созш с

^Fc9 ^с08ш. cos^t- op) '

 

(4.11) (4.12) X. О Z, напри-

Рис. 4.6. Схемы сил, действующих при внедрении клина: а,б,г - при перемещении клина относительно неподвижного тела; в - при переме­щении тела относительно неподвижного клина

Спроектируем силы сопротивления резанию на оси Л и Z:

F^' = N₁ cosy + Fi sin-y + F₂, (4Л0)

_{л T} ^Fi= V^Ni^eiHf^{+ F}i^cosr.

Силы F_x и F^ являются координатами равнодействующего вектора ft:

—»•

ЭЙ ( ю a

Угол ш между R_c и одной из осей системы координат мер, осью Z (С;1), определим по зависимости

COS» г

гпчш- Nrosy -t- F^tHf + fr

{

(4.1з;

F"*> * F'">

X I

 

'Ж1

F„= R.sin.40 X с

in ou

(4.19)

C0S(J*1+W) В системе уравнений (4;15)-(4.19) неизвестными величинами явля-

и

Поис

выражения для определения

Л

Г -, приводит к зависимости (4.20)

где *t_p— касательное напряжение; ^ сЬ~ ОС 6 = (le/svftji^ - площадь плоскости сдвига ОС (см. рис. 4.6); а - толщина срезаемого слоя; в - ширина плоскости сдвига (измеряется в направлении, перпенди­кулярном к плоскости рисунка).

При постоянном значении площади сечения (1 «J) отделяемого объема сила в условной плоскости сдвига зависит от величин <Гр и JJ.. Анализируя их соотношение, приходим к выводу, чго в условной плос­кости сдвига О С касательные напряжения достигают максимума. Это-Ву условию может удовлетворять только одно вполне определенное значение угла в.. Для его определения необходимо найти экстремум функции <U_p= § (J5i).

Из уравнений (4.18)-(4.2О) имеем:

[4.21)

V=-^f ceeCj»i+«»)»**^i-

Найдем первую производную я приравняем ее к нулю:

d^-Ло_ [cOS(Ji₁+oo)c03J» -S*Hj>,5t,ft (J^cufjs 0. (4.22.)

*J»i

 

 

 

Откуда

(4.23)

005(2^ + 00 = 0, Zj»₁+^ = 90°, jj,=TT/4-w/2.

Для случая N," О, F^ = О имеем: R^_n=R_c=- N_t+ F,, и c^J^{3 -} Jf, где ю - угол между осью Z и Ri; J) - угол между R¹ и силой N.. (см. рис. 4.8).

Тогда для принятых условий получим:

ЗТ 1-Г \ (4.24)

Исследования процесса резания подтверждают, что условная плос­кость сдвига в большинстве случаев совпадает с плоскостью макси­мальных касательных напряжений.

Установлено, что с увеличением толщины срезаемого слоя и физи­ко-механических характеристик обрабатываемого материала угол сдви­га Д растет (рис. 4.7). При этом угол действия ш может принимать как положительное значение, когда равнодействующая сил находится ниже оси 2, так и отрицательное, когда равнодействующая распола­гается выше оси Z. Подобное явление наблюдается также при изме­нении переднего-угла (рис. 4.8, 4.9). Обозначения величин на рис. 4.7—4.9 те же, что и на рис. 4.6.

Рис. 4.8. Схема сил, дей­ствующих на передней по­верхности инструмента

Рис, 4.9. Вариант разложения равнодействующей на составля­ющие при большом значении переднего угла Jf

 

Откуда

 

		Л	r-V
	^		'г
J	а
г
Z			Fzt	/ j

Fco

Lt;-Fc8i

 

(4.26) (4.27)

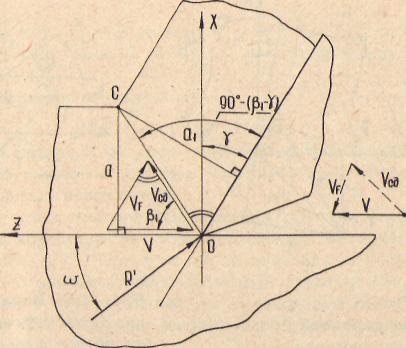
Направление действия сил в зоне резания определяет направление скоростей перемещения взаимодействующих элементов (рис. 4.10). Картина скоростей характеризуется гремя векторами: вектором ско­рости главного движения V, вектором скорости перемещения струж­ки в плоскости сдвига V,g, вектором скорости перемещения стружки относительно передней поверхности инструмента V.. Из рис. 4.10

'сЗ

находим:

SiH(90"-y) Sin^90°-Cji₁-f)] SiHjl,

V_F= Vsinji,/[cos(ji,-y)];

 

[«*(&-*>]

Рис. 4.7. Условная схема изменения сил при переменном значении толщины срезаемого слоя

у V CO S v

C3⁼ '

(4.28)

 

 

L

(4,25)

В итоге начало сдвиговой деформации характеризуется следующим

 

 

значением угла у>.:	37 + °°
	J»i - 4 - г •
При Rc«Rnn	JV-zr- г

Кроме скоростей t", tr., f-g перемещение стружки определяют скорость расширения стружки тг_рс ~ TC05Y и скорость скольжения стружки 0^,_сс⁼ tr$Ln ¥. При всех изменениях скорости 1г_сЭ (она может иметь значения как меньше, гак и больше скорости главного движе­ния) скорость V_pt остается постоянной, V_pc- tr tost¹. Скорость же

 

сил, могут быть установлены на основе предварительно' проведенных экспериментов. Наиболее часто они имеют вид степенной функции, на­пример:

Р „£/„"• (4.29)

где С - постоянный коэффициент, зависящий от свойств обрабатыва­емого материала и условий резания; $ — угол резания; а — толщина срезаемого слоя элемента; т — показатель степени.

Используя формулу (4.2 9), можно установить элементарные силы, если вычислить произведение удельной силы на величину элементар­ной площадки поперечного сечения отделяемого элемента. После этого математические выражения соответствующих проекций F_x, Fy, F» равнодействующей силы можно получить суммированием каждой группы элементарных сил.

Проследим приведенную методику установления силовых моделей на примере наиболее типичных случаев обработки резанием (для крат­кости ограничимся рассмотрением силы F»). Вначале рассмотрим случаи, когда параметры сечения срезаемого слоя (Л, в) есть пос­тоянные величины. Это наблюдается в таких случаях резания, как то­карная обработка (рис. 4.11,а), сверление (рис. 4.11,6) и др.

Рис. 4.10. Картина скоростей в зоне резания (перемещение срезае­мого слоя относительно инструмента)

'"ее ^{меняегся в} широких пределах: от величин, меньших, чем ViKnv, до значения, равного скорости главного движения, 1г_сс * 1г _ — тг.

4.2. СИЛОВОЕ И ЭНЕРГЕТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА РЕЗАНИЯ

4.2.1. Силовые модели процесса»

резания на основе удельной силы

Силовая модель процесса обработки резанием строится на основе равнодействующей R и ее составляющих F-, F„. F», получаемых при разложении R по осям системы координат X V Z • При этом за ось Z системы принимается направление вектора скорости главного движения. Перпендикулярно к оси Z в рабочей плоскости проводится ось X и перпендикулярно к осям X и Z располагается ось 9.

Математическое выражение силовой модели процесса резания R_c = — j(F_, Fy, г») значительно упрощается, если принять, что в направ лении каждой из сил F, Fu, F действуют удельные силы ^цЭ(х)' УЭСИ) ' ЧЭСО • Зависимости, необходимые для определения удельных

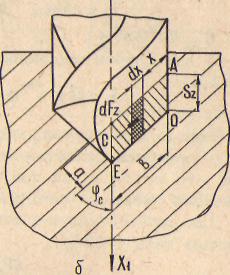
Рис. 4.11. Схема процесса резания при постоянном сечении среза: а — токарная обработка; б— сверление

Для решения поставленной задачи выполним следующие действия: 1, В поперечном сечении отделяемого элемента выделим элемен-

 

 

тарную площадку. Для рассматриваемых случаев точения и сверления такими площадками в параллелограммах ОАСЕ будут участки, имею­щие размеры dx и а. Площадь каждого из них равна cLj:

df = cUa. (4.30)

2. Определим значение элементарной силы dF₉, действующей в
направлении силы F,:

<^x=^F9aw<*f- ^(4>31)

Используя зависимости (4,29) и (4,30), получим:

Л? =Ц-*4**С&-^т6к. (4.32)

3. Найдем полное значение силы г». Суммирование элементарных
сил проведем методом интегрирования зависимости (4.32):

4 %. (4.33)

о о

где f - площадь поперечного сечения отделяемого элемента, £ = = аб (рис. 4.11, 4.12).

Заменим в выражении (4.33) параметры a, б через подачу s и глубину резания t. В результате получим:

а) для случая токарной обработки при a = S sin if; б =Т/9*Л«р
(рис. 4.11,а):

где С _FZ = cfoiK¹^;

б) для случая сверления при a = S_ sin if, 6=t/sirt(f (рис.
4.11,6):.-•"■..*-«»+ pi J-»i

Рассмотрим случай, когда толщина поперечного сечения отделяе­
мого элемента является переменной величиной, а ширина — постоян -
ной, что наблюдается при фрезеровании цилиндрическими фрезами с
прямыми зубьями (рис. 4.12). $

Для определения элементарной силы d F, воспользуемся зависи­мостью типа (4.31):

^dFx=^F^cx>^d;fc*)>. ⁽⁴-³⁶⁾

где df,.- элементарная площадка, произвольно принятая в попереч­
ном сечении элемента, отделяемого одним зубом фрезы (в соответ­
ствии с рис. 4.12 имеем: df_tt) = dBa^); F _а - удельная сила, дейс­
твующая в направлении силы F» со стороны одного режущего зуба
фрезы, \

С _С5_. (4.37)

A1 Qyi

Рис. 4.12. Схема процесса резания Рис. 4.13. Схема процесса ре-
при переменном значении толщины зания при переменных значениях

среза толщины и ширины среза

Для определения переменного значения толщины поперечного сече­ния отделяемого элемента а_ы воспользуемся рис. 4,12:

^aYr-^?^si,l^ ^{= s}x^siH<f_x.

где lr_1s, - скорость перемещения заготовки, м/мин; п - частота вра­
щения фрезы, об/мин; г - число зубьев фрезы; у - угол контакта
зуба фрезы с заготовкой. *%

После подстановки данных и преобразования зависимости (4.36) получим:

dF^Cfis^sift¹"*¹^ de. Полное значение силы F найдем методом интегрирования:

 

0

где J = 6a«, = eSjStH^— площадь поперечного сечения отделяемого
элемента (рис. 4.12). •

Рассмотрим случай фрезерования цилиндрической фрезой с винто­выми зубьями (рис. 4.13). Толщина и ширина отделяемого элемента в этом случае являются переменными величинами. На участке контак­та передней поверхности зуба фрезы с заготовкой К К,К.К, (на виде сверху площадка контакта винтового зуба с заготовкой показана в развертке) выделим элементарную площадку ct| = au/ аХ.

Элементарная сила dF«» действующая в направлении силы F, (а также вектора скорости главного движения), представляет собой произведение удельной силы Р_иЯ на площадь элементарной площад­ки d&, перпендикулярной к F^aT.) • ^и соответственно отличающейся по размерам от площадки d f. Из рис. 4.13 имеем:

dj^ = dj cos w = a y_x dx cos u). Определим удельную силу Fyg,-.» > действующую со стороны вин­тового зуба в направлении силы ctFujg • По аналогии с (4.37), за­висимость для ее определения имеет вид:

где a_w - среднее значение толщины пятна контакта винтового зуба с заготовкой;

^a<e_cp=f/e_p' (4.39)

где £ - текущее значение площади пятна контакта зуба фрезы с заготов­кой; 6_р - длина участка режущей кромки, контактирующего с заготов­кой.

Из формулы (3.27) имеем:

■^(SjR/slKUJ^COS^-COS^), (4-40) '

а из рис. 4.13 находим:

e_P=[^RU'2-4VV^siHC0' ^(4,41)

После подстановки выражений (4.40) и (4.41) в формулу (4.39) получим:

a.. = —^-£— le.ae.tu - C0SC1/. 1. <4.42,

= ------ ^а----- (COSCC - C0SC1/,,).

тер Найдем значения элементарной d F„ и полной сил F»

Гер '«С*-*/ *' ^г>

ия элементарной d'l

 

о cos

^F*^s!^d^'J^Fjewe^df,;

V-R

cdX-jF,

'* * ' ИСЧв'Ч*

99cxje^S*^Cf*^dXcOSCO- (4-43)

Проведем замену пределов интегрирования. Из рис. 4. 13 имеем:

dX = Rd<|//siHcO. ⁽⁴-44) •

После подстановки формулы (4.44) в уравнение (4.43) получим:

i

R

И8(*)в sin <*> s

^F*e⁼S ^FH8(«e^s^^sUc<'x^Bd{F sT^T ⁼

«Pi i

■ sin cpj. d tp я

4------- (cos c^ - cos cp8) = F

/•

У9(*)в Sitl со

= F

H3 czje

(4.45)

S3(z)e

Окончательно имеем (при F = "уд..^cosu>) •'

Ct S„'-^WR

1-*u

(4.46)

tftj^v^r^V-"»^)

4.2.2. Экспериментальные силовые модели-

Анализ экспериментальных данных, выполняемых для проверки те­оретических силовых моделей процессов резания, показывает, что в последних недостаточно учтено взаимное влияние переменных факторов. Стремление отразить это влияние неизбежно ведет к значительному усложнению теоретических силовых моделей. Поэтому в настоящее время пока широко применяются опытные (эмпирические) силовые модели, получаемые на основе математической обработки конкретных экспериментальных данных.

Математическая обработка опытных данных оказывается наиболее
простой, если эмпирические силовые модели представлять в виде сте­
пенных функций, например: п

F,.C_f4\_S»<.VVK_fV,

s

F =C_r iA s^9f* У ^F* K., (4.47)

а

 

где С.. - постоянные коэффициенты, зависящие от эталонных условий процесса резания; Кг, - общие поправочные коэффициенты, представ­ляющие собой произведение поправочных коэффициентов, учитывающих влияние степени совпадения реальных и эталонных значений конкрет­ных переменных факторов (свойств обрабатываемого и инструменталь­ного материалов, угловых характеристик инструмента и других).

Обычно в таких моделях ряд факторов учитывается непосредствен­но. Такими факторами в (4.47) являются глубина резания t, пода­ча s и скорость резания V.

Следует отметить, что теоретические модели полезны тем, что по ним перед проведением экспериментальных исследований можно опре­делить перечень основных переменных факторов и оценить направле­ние их предполагаемого воздействия на выходной параметр. На осно­вании же эмпирических моделей без особых затруднений можно соста­вить представление о реально существующей силовой модели. Рассмот­рим, какую информацию можно получить на основе анализа эмпиричес­ких силовых моделей.

Анализ конкретных эмпирических зависимостей показывает, что, как правило, при t > * в них показатель степени при глубине реза­ния t больше, чем при подаче s ■: На основе большого количества экспериментов принято считать, что Хр ^м 1, У- ^ж 0,75.

В эмпирических силовых моделях показатель Степени при скорости резания имеет различную величину, зависящую от значения скорости резания. Как правило, при больших скоростях резания это отрицатель­ная величина («■» 0,15).

Значения поправочных коэффициентов в эмпирических силовых моде­лях зависят от того, влияние какого переменного фактора учитывает­ся поправочным коэффициентом, а также, от того,как рассматривае­мый переменный фактор взаимодействует с другими переменными фак­торами.

Обратимся к значениям поправочных коэффициентов,характеризую­щих механические свойства обрабатываемого материала: твердость, пластичность и предел прочности материала при растяжении. Данные измерения сил показывают, что с повышением твердости обрабатыва­емого материала растет сопротивление внедрению инструмента в заго­товку и все возникающие при этом силы, соответственно и поправоч­ные коэффициенты, увеличиваются.

Однако, как показывает опыт, величина сил растет не пропорцио­нально повышению твердости обрабатываемого материала, а несколь­ко медленнее. Так, при токарной обработке деталей из углеродистой стали с твердостью НВ320 сила F примерно в два раза больше, чем при обработке мягкой стали с твердостью НВ110. Анализ таких дан­ных позволяет сделать вывод о том, в какой степени силы зависят

от твердости и в какой — от пластичности обрабатываемого матери­ала. Чем выше пластичность материала, тем больше его необходимо сдеформировать при резании для достижения условий, при которых возможно его отделение. С повышением твердости стали ее пластич­ность падает. Если повышение твердости действует в сторону увели­чения сил, то снижение пластичности, наоборот, в сторону их умень­шения. В результате этого силы в зоне резания увеличиваются не пропорционально увеличению твердости, а медленнее.

Хрупкие металлы обрабатываются легче, чем пластичные. Так, на­пример, сила F при обтачивании деталей из чугуна приблизительно в 1,5—2 раза меньше, чем при обтачивании стальных деталей той же твердосги.Это объясняется тем, что при обработке хрупких материа­лов срезаемый слой пластически не деформируется. Он скалывается, и стружка образуется в виде отдельных, не связанных друг с другом кусочков. Достаточно точно о величине сил при обработке хрупких ме­таллов можно судить по их твердости.Так.при точении чугуна сила F-возрастает примерно пропо рцион ально квадратному корню из числа твердости НВ (К _F - "\f Н В).

Важную информацию можно получить на основе анализа поправоч­ных коэффициентов, учитывающих влияние предела прочности при рас­тяжении <^_в. Легче обрабатывается та сталь, у которой меньше пре­дел прочности при растяжении и твердость. Однако, например, в опы­тах по токарной обработке сталей с одинаковым пределом прочности Й_в = 80 кГ/мм (800 МН/м) были получены следующие резуль­таты:

углеродистая сталь - НВ 242, F_% = 260 кГ (2600 Н);

аусгенитная сталь - НВ 170, F = 310 кГ (3100 Н).

Анализ подобных данных позволяет сделать вывод о влиянии на силовую модель процесса резания внутреннего состояния структуры металла в исходном состоянии и о возможном ее изменении в процес­се резания.

Аусгенитная сталь более склонна к наклепу, чем углеродистая. По­этому, несмотря на более низкую исходную твердость аустенитной стали, возникающее в процессе резания повышение твердости приво­дит к тому, что для отделения срезаемого слоя надо приложить силу F- гораздо большую, чем при обработке твердой, но не менее подвер­женной наклепу углеродистой стали.

Представляет интерес сравнение значений поправочных коэффициен­тов, учитывающих влияние переднего угла. Величина переднего угла оказывает на силы самое непосредственное влияние. Этот вывод мож­но сделать, если учесть, что значение переднего угла входит в форму­лы для расчета сил (например, см. (4.33), где 8 = 90-у). С увели­чением переднего утла г уменьшается угол резания S, а следова-

 

тельно, и силы в зоне резания. Одно и то же увеличение переднего угла дает большее снижение сил при обработке пластичных материа­лов, чем при обработке менее пластичных или хрупких материалов. Увеличение переднего угла дает тем меньшее снижение сил, чем вы­ше скорость резания. Кроме того, при резании, например, толстых стружек металл деформируется не так сильно, и поэтому в i этих ус­ловиях влияние угла г на силы менее ощутимо. Если при увеличении переднего угла у протяжки от О до 10 сила F, уменьшается прибли­зительно на 3 5 %, го такое же изменение у токарного резца дает уменьшение силы F, только на 10—13 %. Это явление может быть объяснено тем, что при протягивании толщины среза составляют со­тые доли миллиметра, а при точении, как минимум, десятые доли.

Наиболее существенное влияние передний угол оказывает на вели­чину силы Fj. (см. рис. 4.6,г). Увеличивая передний угол, можно уменьшить силу F_ не более чем в 1,5—2 раза, в то время как сила F_x может уменьшиться в десятки раз. Это явление объясняется сле­дующим образом. При N₂= О, Fj, = О сила F^= F^OSy-N] Si И J" (рис. 4.6,г). Сила F, COS У, действуя на резец, перемещает его от обработанной поверхности. Чем больше угол У, тем меньше си­ла трения F. и тем меньше COS Г • Поэтому с увеличением у F, COSJ* уменьшается. Но при этом увеличивается составляющая N. si и У i направленная противоположно F₍COS у, за счет увеличе­ния Svtty (при одинаковом с F^ уменьшении силы N,).

При достаточно большой величине переднего угла и хорошей смаз­ке, дополнительно снижающей силу трения F|, режущий клин не бу­дет отталкиваться от обрабатывающей поверхности, так как сила F_ получит обратное (отрицательное) направление (см. рис. 4.9). Появ­ляется возможность самопроизвольного углубления инструмента в заготовку изделия. Подобные явления встречаются, например, при протягивании в процессе сверления и в других случаях.

Таким образом, силовая модель является отражением целого ком­плекса явлений, протекающих в процессе резания. Исследование си­ловых моделей является одним из путей познания сущности процесса резания.

4.2.3. Энергетическое моделирование процесса резания

Для удобства исследования совместим мысленно картину скоростей (см. рис. 4.10) с системой сил, действующих на передней и задней поверхностях инструмента (рм. рис. 4.6,г).

В результате нетрудно прийти к выводу, что энергетическая мо­дель зоны ортогонального резания складывается из затрат энергии на участках действия трех пар сил и скоростей:

 

2) F,, V.;

3) F₂, *.

Общая же работа сопротивления Д', совершаемая в единицу вре­мени в зоне резания будет равна отрицательному произве