Приведенных наклонно к осям инструмента

It i оометрии режущих инструментов имеется большое количество i i-i, w которых положение секущей плоскости задается либо линией ^•оичония секущей плоскости с координатной плоскостью и осью ко-

...... it, либо двумя линиями пересечения, например, линией ОЖ и осью

M_v или линиями ОЖ и ОЕ (см. рис. 2.15,а).

Методика решения задач в этом случае практически не отличается I от приведенной ранее:

1) устанавливают уравнение секущей плоскости с помощью опреде­лителя третьего порядка;

2) находят координаты линий пересечения секущей плоскости с дву­мя другими плоскостями;

3) определяют угол между линиями пересечения. „
Для случая, когда секущая плоскость проходит через У„ и ОЖ,

при определении угла между передней поверхностью и плоскостью X yQZ у поэтапно имеем:

1. X sin д - Z cosu = 0;

2. f[cos&cosX cosy; - (.- sinAstnA'Cosi' + cosucosAsLn.ipjsiftAcosJlcosy],

LCcosu; 0; sin д);

(2.53)

HI

f

cos Д tqv - sin Л tq X.

При Д= О toy д = tav _{г т},_е. секущая плоскость в этом случае совпадает с главной секущей плоскостью..

Рассмотрим случай, когда секущая плоскость проходит через ось У у и линию пересечения главной и вспомогательной задних поверхнос­тей OF (см. рис. 2.12). Определим угол между проекцией OF на плЛ кость XyOLy и осью Ху

Уравнение главной задней поверхности:

X(ctoetcostp-toJCsvH(f)+ y-Z,(ctQotsin^ + toA.cos4f) = О

или

Хо, + 9 - /Ц = 0.

Уравнение вспомогательной задней поверхности: X (taA.₁sinif₁+ cto<i₁c05qj₁)+ У + ZCctQcL_lsiH43-t<iA,₁cos<f,) = 0

или

Ха_г + У + %с_г» 0 •

Координаты линии пересечения задних поверхностей:

DF = [Сс,+ с_г);- (^o^ajC,); (a, - а_г)]. Координаты проекции вектора OF на плоскость XyOZy".

QF/X_v0Z_v= [(с,+ с_г); 0; (а,- а_г)]. Угол ш между осью Ху и проекцией линии пересечения задних пс верхностей OF/Xy 0Z у найдем по зависимости:

сг

"УСс,+ сОг +• Са,-аг)г'

cos (О

 

U2

о, -

SttvOJ =

Чс^+с^Чса,- а_г)г "

a,-cu ctaAcosq>- tgXsvnip-tg AjStnq^-ctgdycosify 3 ^С\ + Ь1 ctqAsinif +toA,cos4?^+ctq°4*in4>₁- to^ cos'tp.,

2.5. ПОВОРОТ РЕЖУЩИХ ИНСТРУМЕНТОВ В СИСТЕМЕ КООРДИНАТ

2.5.1. Общие матрицы поворота

I '.'и осмотрим изменение координат вектора, проведенного из начала |рдинат, при повороте его относительно осей системы координат. ' рлчиваемый вектор представляет собой сумму двух векторов —

собственных проекций на ось координат, относительно которой 'I (водится поворот, и на координатную плоскость, перпендикулярную

и поворота., Дли вектора ОВ (см. рис. 2.13,а), например, имеем:

____ ob=ob/xoz + о^/У = oS/xoa + o5/z = OB/yoz+ ОВ/Х.

|

ц|н'мя поворота вектора относительно оси координат проекция век—
i на ось остается неподвижной, а проекция его на плоскость пере-
""...... тся по окружности.

положительное направление поворота, как это принято в курсе й математики, принимаем поворот вектора против часовой стрел­яй смотреть со стороны отрицательного направления оси, отно-,но которой производится поворот.

ч-мотрим поворот вектора О В относительно оси 9. При повороте овой стрелке (рис. 2.16,а) проекция вектора на плоскость X0Z ожения 0В' = (Х_о; 0; Z₀) переходит в положение 0B.j= (X^OJZ,). том сам вектор из положения Оо* (.Х_о; У„^ % ₀) переходит в по— икс 0В*ц= (X; У; Z, ). Н^айдем значения новых координат век-г | 0В. Для случая поворота вектора 0В относительно оси У на I i J3 зависимости для расчета новых координат вектора будут выг-i ж*"|ь следующим образом:

у у0;

X. = R cos (л.

РУ:

Z, = R sin (Д, -J3).

■; sin^s

__ ___—,.------------ *°___ • sl«.A.=--------- -°

У О

т

tx>

ч

Ы

 

U

 

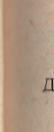
B'Uo.O'.Zo)

Ва(0;Уг'Дг)

B4o;y.;z<)

Bcm(Xi'.o;zi)

B4Xo;o;zo)

^;£з

и
в'(х«;У2',о)\	х2	""т\	/У»
ВЫХзЖ	))\	%ъ/

Рис. 2.16. Схема поворота вектора в системе координат: а - относи­тельно оси У по часовой стрелке; б - относительно оси У против часовой стрелки; в — относительно оси X против часовой стрелки; г относительно оси Z. против часовой стрелки

После подстановки получаем:

%*%', —X_t=X_gco3j> + Z_eitn$; U,sZ₀cos-j»-X_eelKj».' (2.55) Рассмотрим поворот вектора О В против часовой стрелки (рис.

2.16,6):

Ч ж У •

т X, = Rsltv (Д, + JJ)= Z₀cosj» + X₀sinja. ivt.56)

При подстановке в (2.56) отрицательных значений угла поворота,что соответствует повороту вектора по часовой стрелке, получаем систем

уравнений (2.55).

Аналогично (2.55) и (2.56), при повороте вектора О В относите,

■О оси X против часовой стрелки на угол <о имеем (рис. 2.16,в):

t У_г=а$1к (Д_г+ ЗГ) = U,cosS + Z,siHQ';
-*%_г=- Rcos(i_z + «)= 1_ttosS - 9, svnff. (2.57)

Повернем вектор OB относительно оси Z на угол X против часо­вой стрелки (рис. 2.16,г):

£j * ²г; (l)tXjs Rsih, (л_{3 +} х)= Х_гсо5<с+ У_г»*«,т;

S 9j = Rcos (д₃ + г)= У_гсо5т: - Х_гв1лЧГ. (2.58)

Зависимости (2.56)-(2.58) справедливы также для расчета коор­динат векгора при повороте непосредственно системы координат в сто­рону, противоположную повороту векгора.

При повороте вектора О В по часовой стрелке, а системы координат против часовой стрелки значения углов в, j», tr необходимо в сис­темах уравнений (2.56)-(2.58) брать с противоположным знаком,

■ читая, что поворот производится на величину отрицательного угла.

Анализ различных схем поворота тел и режущих инструментов в

■ in теме координат показывает, что для поворота режущих инструмен—
РОВ наиболее приемлема схема У — X — 2.. По сравнению с известной

схемой поворота У— X — У', разработанной Эйлером, при повороте по схеме У — X — % относительно каждой из осей производится, как мини­мум, один поворот, что имеет положительное значение при исследова­нии геометрии рабочей части инструментов.

Составим общую матрицу поворота по схеме У - X — *.

Для первого поворота на угол (8 относительно оси 9 (системы X9Z по часовой стрелке, векгора О В против часовой стрелки) имеем:

"i ⁼ Уо 1 -*■ Х₁₌ X₀co3j3-Z₀stnja |

t I.

COS

Р-

(2.59)

ля второго поворота относительно оси X на угол <5

,SiHjD + £₀

w

X₀cosjd - 1₀ sinja;

-*■ 2_г= Z,cos6- y^eiri.6 = (X₀siH.J3 + Z₀cosj3)cosS'- 9₀siH(o; t 9_z=Z.,sin<5 + b₁cos6' = (X₀sin.p+2₀cosj))sinG+ У„cos€Г.(2.60)

1ля третьего поворота относительно оси Z на угол V:

 

 

f У= а"со««- z"si»v<?. Поворот относительно Z на *■■ Z"1; I X"=Xmco»-c-ymsivc;

(2.64)

(2.63)

SL = У^соз* - Х,*1кТ = [(2₀cosj!> + X_osi,tiJi))$vn^+ y_ocosS3cost-(X_ecosj3-

-I_esir,j5)_SiK<t_; (2.6.1)

Xj= XjCost; + aj9v«,⁽C = (X₀cosjs-Z₀sltvJ>)costi-[Cz_ocosja + X₀»in,p)sinS +

+ y_ocos(s]svn.<C,

В итоге общая матрица поворота вектора или системы координат схеме У — X — Z имеет вид:

Х, = Х =X₀(.cospcos'S+sin,p6iH'B')+ Ujcosefsinli 4

(2.62)

+ Z₀{tosp *{,*,<$ tint - siKjacost); У_}= y'=X₀(slnp sin.Scos'B-cosp stu<o)+ y_oeos6cos<C +

+ Z,_o(coe_ip»in.«fcos^c3+ sitvp»itvt); Z =Z a Z₀coejs cos£ •+ X.sCttj9co6(if- Ч_сЫп<3,

где X., Я, %.— новые координаты точки вектора в старой системе

X У Z > X'" i У^т. X¹"^- координаты точки вектора в новой повернуто системе координат X У!«,„_„». -

Задачи на поворот системы координат относительно режущего ин­струмента связаны также с выражением старых значений координат рез новые. Рассмотрим методику такой замены для случая последов тельного поворота системы координат по схеме У — X — Z (рис. 2.1

б,в,г).

1. Поворот относительно оси У на угол+jj:

/

У₀=У;

t

i,Z₀=X'co5js- x'siwp;

_Х =X'cos^ + Z'siHja.

2. Поворот относительно оси X на угол +6:
Х'=Х" | /

угол ум •»

7 (2.65)

/

Ч~у

В У"=У'"соа<Г <-X'"svni!.

T

_Xui х^и

Общая матрица для выражения старых значений координат через 1>вые при повороте системы координат по часовой стрелке по схеме - X — Z приобретает следующий вид:

У >У'=у"соа«5- Z"siH<?«ty"Wt + X"^,Stne)cosS- Z'"»in<J;

О

Z,₀=Z'coeja- X'»vnj3=(.Z"eo»<?+y"»in(5)co4j>- X^HiiWjp «= [Ус> + ty"»»li t Х^,и*1*.1П»in«]cosj3-(X^,,'cos'E-y^,,,siH/!r)sifvp =

В X"eos⁽ocosp+ 9^mcos'CcospSia^ + Xsvn'Scospei<it(J-X^mcoS'o eitvj> + + В^1И51лЧ! stnjs = X"¹C»in'Coosp9in6'-coe4JsiKj»)+y^mCco»T;cotjsco»ff +

+ sim;*<,nj5)+ z'"co»S cosj»; X₀-X'cosja+5t¹9inj» = X^,,coeja + (X^llc(JS<3+ y"9inef)8ittjs =

= (X^mcos'D- 9"'siw,<Oco4p + [z'"cos(S + (y'"costitX"^,»iH<c)»vt_v^]sUj3 = = Xcostcosp- y'"stn.T;co»,p-t-Z"ko9<5»inp+ y"cos<B»iti€»i«,_p + +X^ll,sin1svu<S»l«,j» = X' (costeoep+ sin's SiПб SiHp) +

+ y^l"tcos^,esiH(JsiH(S-Si.n'C tosja)+Z oosSsinp. (2.66)

При повороте вектора или системы координат по любой другой схе-0 значения координат Х₃, У_д, 2, и X'", У"', Z'" в матрицах поворо-

будуг другими.

Рассмотрим пример. Пусть единичный вектор О С, лежащий на оси X, поворачивается в системе координат X У Z один раз по схеме $ - X, а другой - по схеме X - У.

На основании (2.56)-(2.58) имеем:

 

_^Х'=1*со5б+ y"si«,<a;

Ч

^0C<(.n-af^i^=cos6sin-^!8' ⁹_г^=в1н^^; Х^созрсозб). Это происходит потому, что б¹, т; i га — углы поворота не самого вектора О С, а его проекций на соответствующую координатную плос­кость (в зависимости от схемы поворота).

2.5.2. Примеры поворота режущих кромок и рабочих поверхностей инструмента в системе координат

Приведенные выше матрицы поворота справедливы для любой систе­мы координат. Поэтому при рассмотрении примеров поворота будем ис­ходить из некоторой произвольно взятой системы координат X J Z, в которой кромки и рабочие поверхности определяются координатами, характерными для базовой системы координат Х_уУу£у.

Рассмотрим в качестве примера изменение координат вектора, пер­пендикулярного к передней поверхности резца, и единичного вектора, лежащего на главной режущей кромке, при некоторых видах поворота резца в системе координат.

2.5.2.1. Поворот относительно оси У на' угол +ja.

Исходные данные:

1. Уравнение передней поверхности:

X cos(.if + е)+ УоЦу cose- Z siu tf + t),

^где v^irV-

2. Координаты единичного вектора, лежащего на главной режушей

кромке:

ОЙ* XXX = (cos A. svntp; si.fi A; cos X cosif).

При повороте вектора OB относительно оси У на угол +jj (0 = О и 1 * О) новыми координатами его в соответствии с (2.62) будут:

X.= coslstH((!cos_ij>-cosl<uOS^ siup = cos J, siuC^^- J³)',

4,= sin X;

X, = cosAcosipcos,p + M>sA.si'H,ip sin.j»=oosA,cos Cif-J»);

OB. tX^X = [cosAsi-tvOf-p^sinV, cos A. cos (.if-ja)].

Вектор П > перпендикулярный к передней поверхности, имеет следу ющие начальные координаты:

П£ ХУХ= [cos (if + ty, ctoj cosf,-sinlip + E)]= (а; в,- с). При повороте резца в системе координат X У Z относительно оси У на угол +js новыми координатами вектора tt. станут:

Чт)^бт= <% ⁶г-^с<>;

a₁=cos(4^,+ e)cosjs+ Svh ce+(p)siHjs = соэ(ц>+ e-j») = cosCP-f-e); f^ctgycoee;

c₁₌ coscif+eisitt-j» -sinc*f + e)cosj» = sincja-f - ^e)-

2.5.2.2. Поворот относительно оси X

Для получения новых координат можно воспользоваться уравнением (2.62).

Применительно к уравнению передней поверхности имеем:

a^= cosCif+E);

в, = cto у cos е совв - sin Сч+ е) silts';

с, =- sin Ctf+e) costf - ct<jj- cos £ si«,e\

оотвегствующим образом изменяется и уравнение передней поверхнос-

XcosC(f+e)+ У [cto г cosecos<5-aittC(p+e)&i.n6]--Z [ei,HCif+t)cos6+ cta^cose sin <э] = 0

2.5.2.3. Поворот относительно осей V - X -Z

Рассмотрим э тот случай на примере поворота единичного вектора QB, лежащего на главной режущей кромке:

X, = coslsinif«:osjacos't + Si/Uj9si,u6 st*U)+ sln.A.cosdsin⁽o + + oos^cosi^(,-svtvj» cosTi+ cosjssinS sitvt) = = cosJlsirtu>cos_<peos^tC -cos^sltup sin. <3 s^"-^ sittja +

+ Sin Д, COS ^Sin<C-C0sXcOSip StttjD COS'S + cosJ.coefpcosjOsitidsln.'Cs scoS^CoST: Sitv(lp-ja) + COsl SiHirs;.tv6coS((j>-p)+8irtlcOSd.S{.n'(7;

 

I

НН

У =-coslsin<f cosjjsWC + coslelnipeifipstnffcos'o + -t-svnAcosScost; + cos A- cosip cosp sitt£ cost +

+ cosAcostf slnpsvnT; =-cosAsi»v'CaiiKC4'-j») + + cosAsiftefcos'ocosc<p-ja) + SiH Л cost» cost; ZjecosA6in<f>sinpcos<» + coslc«s<f cosecos^~sin4,siw^ ₌ =*cosA cos6 cosc<f-jo)-siw A- sin(3. В результате единичный вектор OB, лежащий на главной режущей кромке, после поворота его в системе координат X УХ против часо­вой стрелки по схеме У — X — Z получает следующие координаты:

cos A cost «ia (4>-j8)+ cosAsin'Min6cOS(ip+jB)+- + sinA cos <5 sin's;

*.(y-*-Z)

+ cOsXsin<CSvnCtf-J>); cosAcoegcos cif-j'J-iittAstne'-

ft

ки получаем:

Аналогично при тех же условиях для вспомогательной режущей кром-

Of eXU eCcos^sin^i-svn^ ', -cos^coscp,). cosA₁cos^tCsln(ip₁+j3)-sinA₁cos<9 svnt -

(2.68)

05<й-х-г)бХ^=^

- cos Of,+J») cos A-₁ sin б si n't; -(cos с^+рэсоаЛ-^пбсовт; + + cosA-₁eiH'usirt(tf_l+j8)+cos(ocos'0sinA₁; sin A, sIk(o - cos^ cos <S cos C^ + J»).

2.5.3. Изменение в процессе поворота

углов,характеризующих положение режущих кромок

Рассмотрим изменение углов, характеризующих положение режущих кромок инструмента, на примере поворота рабочей части резца относи­тельно системы координат.

Выведем формулы для расчета величины углов наклона главной и вспо­могательной режущих кромок после поворота резца по схеме У - X - * ■

Найдем углы 1.^._х.., и Aw м_х-т) • Д^ля этого воспользуемся координатами грех единичных векторов:

J - (О; 1; О), лежащего на оси У системы координат X У Z, 06 и 02, расположенных на главной и вспомогательной режущих кромках.

Угол Ai (N_y- г) определим исходя из того, что угол между j и но­вым расположением О В равен 90 — Хл (n-x-ZI •

Так как j»(0; 1; О), а О^в*(у__х_х) ^m^V *V ^8 '* ^полУ^чаем:

cos[90»-X_<(s._x._X)] =

Поскольку выражение "^ (Х«)^г + (У,)^г+ (Z,)*'"^м 1» получаем: sUA^ _ty__x^,₎=siftAco*6co5^,C +

+ cosAsin6costcosc<f-_vp)-cosXsin'E Ctf-j»). (2.69) _t По аналогии, используя новое положение единичного вектора OIL л. „ _., лежащего на повернутой вспомогательной режущей кромке, j «(О; 1; О), значение угла А^. («.X-Z5

и ко'ордйнаты вектора

определим исходя из следующего соотношения

А,

s*HA₁{(SI_X-i)^=c0SCtp₁+j3)C0sA,₁sin(acos^,G *

+ cosA₁SvH'o svh((j>_i+j3) + c0s6cos'C8vhA.₁. (2.70)

Частные значения углов наклона главной и вспомогательной режущих

кромок (например, А^ _tx);^К1У) ■ ^f QC-Z) > ^11 СX-Z) ^{и г}'^д") вытекаю' из полученных выше уравнений (2.69) и (2.70) при условии, что в

зависимости от схемы поворота некоторые из углов поворота (J8, д?, «С) принимаются равными нулю.

Частные формулы можно получить также путем решения задач не­посредственного поворота. Определим, например, величину угла

А^ _w', ОБ = Ccos A, sin у,; - sin А,; - cos A, cos cp_n).

После поворота относительно оси X имеем:

(2.71)

X^cosA,- sin<f.,; a^-sinXtCOsS-cosA^cos^sinS; Z_s-- cosA^os^cosS +sinA₁sin6;

ОБ

UX)

C*1» M> ^1'i

svnA_1l№= siw^costf + cosi, coscf₁ sine.

 

Зависимость (2.71) полностью совпадает с (2.70) при JJ •* О и

Определим величину углов в плане режущего инструмента <р^ («_«_,. ₍ %i (м-х-г) • ^<~^>ни Р^{асполагаюгся} между проекциями режущих кромок на плоскость'XOZ и направлением подачи, которое в большинстве слу­чаев совпадает с положительным направлением оси Z системы коорди­нат.

Найдем угол между проекцией вектора ив на повернутую плоскость и XOZ* ty-%-z,) ^и единичным вектором, лежащим на оси Z, т.е.

В новой системе координат, повернутой относительно осей У - X —
— Z, проекция единичного вектора ОВ на плоскость XOZ. _(Ч. имеет

следующие координаты:

o"S/XOZ^_c:(._x__X)=CK^w;o;z¹¹¹);

^x«' = v z'"=v

Единичный вектор К *= (О; О; 1) в новой системе координат, согласно зависимости (2.62), выражается следующим образом:

Кб ХУ1^ _ta__x__Z)= (0;siH6; cos<s).
Угол Ч^и-х-г) определим как угол между ОВ/ХОХ_<_/,₎__х_^₎ и К:
cos6 [costf cos t«p-i>l-tgAsi,n6],

^tS-X-Z.)^Y{»*n.(if-j») cosx + slnt [cose tqA. + si-nScos Cif ^p>Jl-*+ (cosScosCtp-pJ-tgA st»^]⁴

По аналогии с if.,„ _x_ _г), угол f₍<(u_x-z) ^найдем как угол меж­ду проекцией вспомогательной режущей кромки на повернутую плоскость XOZ и вектором (- К), лежащим на отрицательном направлении

и-KeXU

Us-x-z)

x-z)

оси Z, т.е. угол между ОЛ/XOZ^ _С!)_

cosgfcosficosd^tpi-tq Justus]

Щи

(2.73|

X на угол ь. Вектор jeX^Z = (О; 1; О) в новой системе коор­динат (X У Z)^(х) имеет следующие координаты: 7е(ХУХ)_1(х)= (0;cos<3' -itntf).

Вектор j е XVZ.,., лежащий на новой оси iL (х) > в старой си­стеме координат х у Z определяется следующими углами: J eXVZ_nx) = (0;cos6; ₅гн<э). Напишем уравнение плоскости, перпендикулярной к f: 9cos<5 + Zsine "Р-Проекцию единичного вектора 0 6 > лежащего на главной режущей кромке, на эту плоскость найдем как результат ее пересечения с плоскостью, проходящей через DB и j. Уравнение последней оп­ределим, решив определитель третьего порядка:

coslsinif; sitvA; eosAcasif

0; cos6; si-пб; «О,

X У Z

X (cos6cosip-tQAsin6)+ysvnGsitt_T-ZsiH<pcos(3 =0.

Составим уравнения линии пересечения двух плоскостей:

X(cos6cos<f-taAsin6)+ysiH6sin(p-ZsiHificos6 = 0, У cos<5 t Z Stн<у =0-

a,X +е,У+ c,Z=0, «,У +Cj,Z = 0.

 

Рассмотрим вывод ряда частных зависимостей. Для примера рас­смотрим получение зависимостей для расчета углов (j>* /„. • %t (х) > fyty-X* ' fitfZ> '^tfX-г) ^{и т,д}* Подобные зависимости можно получить, принимая в формулах (2.72) и (2.73) значения углов <t, 6,а в со­ответствующих случаях равными нулю.

Однако с целью проверки уравнений (2.72) и (2.73) изберем дру­гой путь. Используем для определения уравнений проекций режущих кромок на повернутую плоскость X О Z метод нахождения линий пере­сечения двух плоскостей: плоскости, перпендикулярной к повернутой оси У, и плоскости, проходящей через режущую кромку инструмента и повернутую ось У.

Рассмотрим вывод формул определения углов Vwy} и fiffxi '

Повернем систему координат по часовой стрелке относительно оси

+ c.

В итоге линия пересечения (Л П.) имеет следующие координаты:

ЛП^= fsvtup;-(cos6cos(f-tgisvH6)sin^■, (cosecosip-toA sinejeostf].

Искомый угол IB, расположен между осью Z и Л П.:

(cosiftos6-tg3,5in<5)cos6
tflitp =-==" ³ г- (2.74)

^ux) ysiK'ip + Ccostfcosif -taAsineO¹

Зависимость (2.74) совпадает с общей зависимостью (2.72) при J>= О и Т= О.

Найдем выражение для расчета угла Ч\<Ш- _»

Запишем уравнение плоскости, проходящей через 01 и j:

 

 

cose; У

j,= (0:, cosff ■, si-иб),
0!D = (cos^siHi^-sitvA.^ > -cbs^cosip.,)
C0SV'^H<?,i -si»V> -cosA, cosq»,

0,

0; X

SiK<3

Z

X(C08fj-ta,te€)-'St'^VvKiftt Zsin^sO. Определим координаты линии пересечения двух плоскостей: XCco's(f-tol,to<S)- ytjgsui^+Zstitcp^O, Усо5<5 + Zsin6*0. ЛП_г= [»1н^/сиб; Ccos4.₁-tgA₁t^6)sin0;-(costp₁-tgA.₁tg6_b:ose]-jJronif.M найдем как угол между двумя прямыми ЛП_ги -Z или

ЛП^и - К«ХУХ

cos».

(2.75)

(О; О; -1): (cos if, -Чд А₁ tt|6) CosV

Выведем формулы для расчета углов vf_t(z) и <^(_г) • После поворота системы координат XYZ по часовой стрелке отно­сительно оси Z вектор fe X V Z< _(z) - (О; 1; О), лежащий на новой оси У, займет положение

}",* XVZ = (-Sih^cost; 0). Как и ранее, с помощью определителя третьего порядка находим уравнения плоскостей, проходящих через j, бХДц₂₎и режущие кром­ки:

" Xcost coscp + У slut cosif-Z (sin <р cost: + sint tol) = 0;

Xcosip t ytQ*cosif, + Z(Hft^-to<ttoV=0. Плоскость, перпендикулярная к JA-XSitVC * ycOSX = 0), с перъой из плоскостей образует линию пересечения с координатами

Ml,?-- [cost(.Svuu>cos^<t + taXsi-Wb)-, sinl (svnifcost +toAsvti/B)-,cos(pj-Координатами второй линии пересечения являются

лп_г= [cos-c csuif_t- to«e toj 4-,); + 9ini;csiu^-t^^<ci^0;-^MS4^l,/^oos'^t^

Для определения углов между осью Z и ЛП,, ЛГЦ и отрицатель­ным направлением оси Z получаем следующие зависимости:

"^St ■ (2.76)

COS

^tos^Jip + (slntpcosfc + tflXivwt)⁴

 

COS Ц?

^COS(fl (2.77)

¹^(^z) ^ COS²^ +•(*<•* If, cost -sittt t^i,¹)⁴
Применяя подобную методику для угловш. и ш., найдем сле-

дующие зависимости: ' '

соэб [co s6co8C^-p)-tj[Xivttg ] (2 78)

*^W"*' ^sih.^sL(?-ja)+[cos(3iC05Ctf-i>)-t^sins']² '

cosfl [costf cos CtyjO- tg^stng 3, ■.

COS 1С..C- j ^v i- fl i g

2.6. МЕТОДИКА АНАЛИТИЧЕСКОГО ИССЛЕДОВАНИЯ ГЕОМЕТРИИ РАБОЧЕЙ ЧАСТИ РЕЖУЩИХ ИНСТРУМЕНТОВ» НАХОДЯЩИХСЯ В ПРОЦЕССЕ РЕЗАНИЯ

2.6.1. Схема образования кинематической системы координат

Образование кинематической системы координат Х_ш У_и, Z._k., опре-
■ „ > WWW

деляющей положение режущего инструмента в Процессе резания и слу­жащей для огсчега кинематических угловых характеристик инструмен­та, можно осуществить как непосредственным построением ее на ос­нове вектора скорости результирующего движения резания, так и ме­тодом поворота статической системы координат инструмента X_VY„Z_V до совмещения одной из ее осей с вектором скорости результирующе­го движения резания. Второй метод построения кинематической сис­темы координат X_wy_wZ_w значительно упрощает методику аналитичес­кого исследования геометрии режущих инструментов в состоянии про­цесса резания, гак как при этом могут быть использованы формулы поворота систем координат.

В системе координат X_WY_WZ вектор скорости результирующего движения резания, так. же как и вектор скорости главного движения в системе координат X \Z._V совпадает с одной из осей системы. Для определения схемы поворота системы координат ПН до сов­мещения одной из ее осей с вектором скорости результирующего дви­жения резания W необходимо прежде всего определить его положение ш системе X_v^_vZ.y.

Рассмотрим пример токарной обработки деталей резцом (рис.2.17).

В принятом случае вектор скорости резания W равен сумме век­торов скоростей главного движения V и подачи V<:

,-Ц----- —4, _ 'w^r="V + v'_s,

где 1^(*Y|?(4]V_S|, JV(- 51 Им, мм/мин, f.^J:*-S',H мм/мин. На-

 

Рис. 2.17. Схема токарной обработки проходным резцом

правление вектора скорости главного движения V зависит от распо­ложения точек режущей кромки инструмента относительно обработан­ной поверхности детали. При точении формообразующая точка режу­щей кромки инструмента может располагаться выше или ниже линии центров токарного станка. В зависимости от этого вектор скорости главного движения для различных точек режущей кромки инструмен­та отклоняется в ту или иную сторону.

Величину угла отклонения вектора скорости главного движения определим по зависимости

siHu) = ih/H, где £ \\ - смещение точки приложения вектора относительно линии центров станка, (+) - выше, (-) - ниже линии центров; В - рассто­яние между начальной точкой вектора V и осью детали.

Образующийся угол у. между вектором скорости резания W и век­тором V определяется по зависимости

Ьш- ^ - ⁵* - ^S,

где s —подача, мм/об; Б - диаметр вала, мм; и. — частота враще­ния вала, об/мин.

Таким образом, в общем случае положение вектора скорости реза­ния в системе координат Х_уУД_у может определяться рядом направ­ляющих углов. Для рассмотренного случая такими углами являются углы из и ц. При известчых значениях этих углов для перевода сис­темы координат XХ1_у в положение X_w*vv^W необходимо исходную систему координат сместить в положение X¹ У_у Ъ\ и повернуть ее

относительно оси Z' на угол ш и относительно оси X' на угол р.

2.6.2. Методика определения координат режущих кромок.уравнений режущих поверхностей и величин углов в кинематической сие теме координат

Методика определения координат режущих кромок, уравнений рабо­чих поверхностей ^ секущих плоскостей и кинематических углов в системе координат " w^w ^ w заключается в следующем.

1. Определяют координаты режущих кромок и др_угих_элементов рабочей части инструментов в системе координат X У_у Z_y.

2. Осуществляют поворот системы X_y^/_vZ_v до совмещения векто­ра скорости резания с одной из осей.

3. Определяют координаты рабочих элементов в новой системе ко­ординат X y_wZ_w с помощью матриц поворота.

4. Находят значения рабочих (кинематических) углов.

При э том определение углов, характеризующих положение режущих кромок в пространстве (рабочих углов А-, JL,., ф„, (fj), сводится к определению углов между отрезками прямых или между прямой и плоскостью. Для определения же рабочих углов, характеризующих по­ложение в пространстве рабочих поверхностей режущего клина инстру­мента (рабочих углов J»,d_p, у. ««'ip)' наиболее удобно использо­вать метод определения углов между линиями пересечения двух плос­костей третьей плоскостью. Так, рабочие передние углы г_ и У. на­ходят между линиями пересечения двух пар плоскостей:

1J секущей плоскости и передней поверхности;

2) базовой плоскости, перпендикулярной к вектору W, и секущей плоскости.

Рабочий главный задний угол at. определяется пересечение!* двух прямых, каждая из которых образуется пересечением двух плоскостей:

1) секущей плоскости и главной задней поверхности;

2) плоскости резания и секущей плоскости. Рабочий вспомогательный задний угол Ы. находится между линиями

пересечения:

1) секущей плоскости и вспомогательной задней поверхности;

2) плоскости, Проходящей через вспомогательную режущую кром­ку и вектор W, и секущей плоскости.

Разберем кратко алгоритмы расчета этих углов, которые без за­труднений реализуются с помощью ЭВМ.

Передние углы рассчитываются в следующей последовательности: 1. Определяют координаты единичных векторов, лежащих на перед­ней поверхности, и вектора W в системе координат X_v 5L Z._y.

2. Составляют уравнения передней поверхности и плоскости, пер­пендикулярной к W. в системе координат X_у X_v Z _v.

3. Находят положение секущей плоскости (например, плоскости, перпендикулярной к проекции главной режущей кромки на плоскость, перпендикулярную к W).

4. Определяют координаты линии пересечения секущей плоскости и передней поверхности,

5. Получают координаты линии пересечения секущей плоскости и плоскости, перпендикулярной к W.

6» Рассчитывают угол между линиями пересечения. Для определения задних углов расчет производится следующим образом:

1. Определяют координаты единичных векторов, лежащих на зад­них поверхностях, и вектора W в системе координат Х_у У_у I_v.

2. Составляют уравнения задних поверхностей и плоскостей, про­ходящих через вектор W и режущие кромки.

3. Находят положение секущей плоскости.

4. Определяют линии пересечения секущей плоскости с соответ­ствующей рабочей поверхностью и секущей плоскости с одной из ба­зовых плоскостей. Рассчитывают величину углов между линиями пе­ресечения.

2.7. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ФАСОННЫХ ПОВЕРХНОСТЕЙ РАБОЧЕЙ ЧАСТИ РЕЖУЩИХ ИНСТРУМЕНТОВ

2.7.1. Определение п о л ожения прямых, касательных к кривым и поверхностям

Рассмотрим вывод уравнений для описания прямых, касательных к пространственной кривой, заданной зависимостью | (X; У; 1) = О, где Х_ = ip(t); у м V (t); % «я ш Ct). Подобными параметрически­ми уравнениями задается в пространстве положение винтовой* линии.

Предположим, что точка М₀(Х_о, У₀, Z₀) этой кривой (рис. 2.18) соответствует значению t, а точка Q(X-t-дХ; У + дУ;2+д£)- значению

t + Д t. Тогда уравнения прямой, М₀ Q в канонической форме име ют следующий вид:

X ~ X ₀ _ У - У о _ X - X о _

дХ д У „" д Z

При делении на дt получим:

^Х " ^Х_°_ Jj " Ц° - ^Z ~ ^Zo дХ/Д-t " ДУ /At ~ AZ/At

Переходя в этих уравнениях к пределу At —*- О, получим уравнения касательной к кривой в точке М₀СХ_о1У₀Х₀):

о _

Z-Zi

dX/dtL' oLy/at|_Mo~ dZ/dtJ^

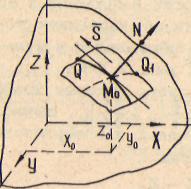
Рис. 2.18, Схема расположения векторов, касательных и нормаль­ных к поверхности

При э том направляющий вектор 3", параллельный касательной, бу­дет иметь следующие координаты:

И

(2.80)

' dt

м₀' dt |м/'

it dt

(Х-Х0)+^-

U-Zo)=0. (2.81)

Уравнение плоскости, проходящей через точку М₀(Х₀У_оХ_о) и пер­пендикулярной к касательной, запишется в следующем виде:

 

М„

Для случая, когда кривая линия^задана уравнением j(X,if) =0 при 9=ip(X), уравнения вектора S, параллельного касательной, в канонической фо рме имеют вид:

х-х, dX

(2.82)

.₌ii_;y-_yo=cty/dx|_MU-K₀).

Величину cdif/dX найдем по зависимости о1У /dLX =—J)

Тогда уравнение касательной к кривой |(Х,У) «■ О в точке "°М.(Х УЛ можно записать так:

Определим направляющие косинусы вектора S-(cBSdjcoipjcos-c);

»-»•■-ifjfjV'-w ^l2'^e3)

Уравнение нормали к этой кривой в точке М_еС*_в,У₀) имеет вид:

Ш§!1 (X-XJ. (2.84)

В e 3f /ЭХ |м.

Выведем уравнения касательной плоскости и нормали к поверхнос­ти ^(.Х,Ч,Х} — О. Возьмем на поверхности обыкновенную точку Mp^X^S.jZ,), в которой pfx i ду ' 8Z ^{не 0}бР^а1н^{ается в Н}У^ЛЬ одновре­менно, и какую-нибудь линию M_pQ (см. рис. 2.18).

Прямая M,N, имеющая в качестве своих угловых коэффициентов значения частных производных 5LL_ J it-L. г grL» вычисленные для точки М_в(Х_в,У_аД₀) • называется нормалью к поверхности ^(X,y,Z)* •О в данной точке. Ее уравнения имеют вид:

 

C05J3

,,,; cosoi = -7= .... —1; гшт-г

2.7.2. Пример расчета передних углов цилиндрической фрезы с винтовыми зубьями

Напишем уравнение прямой А В, образующей геликоидальную по­верхность передней грани цилиндрической фрезы с винтовыми зубья­ми (рис. 2.19). Крайними ее точками являются точки Айв: А(0; R; 0); B(R5vnycosy; Rsiti^jO). Запишем уравнения прямой в канони­ческой форме:

х-х₄ _ ц-ы< _ 2- Z,X - 0 _____________ Я - Я

(2.89)

Xcosr+• У«*пу - fts»«v =0.

 

 

*.

(2.85)

, нормального к поверхности (2.86)

Ц1Щ^ *№\л, *№%