Тогда координатами вектора MQ N, нормалы f(W)- О, будут

Плоскость, касательнаяк поверхности j (Х,9,%) *Ю в точке Ц|(Х^о^е1 и перпендикулярная к вектору М0 N, описывается уравнением

и.

СУ-V+lf I CZ-1₀). (2.87)

М₀ ^п |м₀

Рассмотрим зависимость для описания касательных прямых к линии пересечения двух поверхностей J С^)"»³') ** °J fjtX,3,Z) «" О. Векто­ры N₍ t N,, нормальные к поверхностям f_A и fa, имеют коорди-

Вектор S, касательный к линии пересечения двух^поверхностей, пред­ставляет собой векторное произведение векторов N, и N_t:

•*•		к
9Х	ЭУ П
ш ш ш ЪХ ЗУ ъг

f.t/ tiuia!ffl)

Т.

. м ахах " axaz / (2.88)

\axas as ЭХ / ^J

 

Рис. 2.19. Параметры торцевого сечения цилиндрической фрезы с винтовыми зубьями

Так как угол у равен углу у, го при повороте А В относительно и 2 на угол t будем иметь:

Xoos(y+ti)+ y$iHly+T)-ReinreO. (2.90)

Для вывода уравнения передней грани фрезы используем формулу ижущегося начала [36 "Ь

-^_с (2.91)

1%

Z-

где t - угол поворота; F - шаг геликоидальной поверхности. (Значе-

 

ние «С положительно при повороте прямой А В против часовой стрелки, если смотреть со стороны отрицательного направления оси Z.)

Решая совместно уравнения (2.90) и (2.91), получаем:

Xcos(y--^Z) + ysU(^-^Z)-dstnj. = 0. (2.92) Запишем уравнение плоскости, касательной к геликоидальной по­верхности в точке А (Х₀, У₀₎ Z₀):

А ^>)+Мг

(Z-Zo) = 0,

3J I (Х-Х Н ЗЛ

Ж\Г ^Хо)+ ЗУ

 

cosyR

svnv 0

Для ЛП_г эти же уравнения выглядят следующим образом:
л " ло У ~* У о /С^—>Со

cosy R

■ ^Rcosj F/aor

Stuy--Rcosy-^.0 F/2,3!

F_

);-Rstny).

^ЛПг⁼(-Йг^^нГ'-^С03У(1аГ^т^

Определим косинус угла между Л П. и ДП,:
COSY = cosy (f/2* 4-affR</F)

^fN ^siH^(F7^²+R^z)+cos*r(F/fcnUarRVF)*'

Для упрощения зависимости найдем значение Stny_N и ЩУи •

SiHytF а/43Га+ R*

У5*п£у(Рг/4Лкг)+со5гу(Р/2я+г:пКг/Р)2

^sin_N=

 

Z

Ft

 

Для точки А С D, R_T0) имеем:

X cos у + ilsiny-Z -^ fUosy-Rsinj^O.

Составим уравнение плоскости, перпендикулярной к касательной,

проведенной через точку А (0,(1,0) • Используем параметрические

уравнения винтовой линии (см. рис. 2.19): X^Rsitvp; i)=KC0Sfiil--^rfi-

Следовательно, с1У_ _Bsirtp. dX_ = RCOSJ»; 4~я £- •
dj» ^' d? CIJ3 Ч.Я

Уравнение искомой плоскости имеет вид:

ах

«■-w+#

owyfrjjjl

(Z-Z₀bO;Rcos_ip(X-X₀)-RsiH_>p(9-y_o)t_S:(Z-Z₀)=0.

Для точки A~tO, R,0.) и J3 «О имеем: XR + Jj7 X =0.

Передний угол фрезы 1*_м, измеряемый в плоскости, перпендику­лярной к режущей кромке фрезы, образуется между двумя линиями пересечения трех плоскостей: ЛП, и ЛП_г:

f-Z^Rcosj-Rsiny = 0,

fX=0 fxcosx+ysinf-Zfi

lXR₊Z^ = 0; IXRtZjEj-O

90Z

Уравнения Л П. в канонической форме имеют вид: х-х„ 9 - Уо г- z,

где X = О ~ уравнение координатной плоскости в кан'

bABt-W^-iO).

гя

о

О F/2.3T

У - Уо

Так как F/V F* + 4з?^г R^5, =C0sA. (^ГД^е ^ - угол между образующей фрезы и касательной к режущей кромке), получаем tflVu-taYCOsX. Окончательная форма полученной зависимости полностью' совпадает с полученной ранее формулой (2.49).

ГЛАВА 3

ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ОТДЕЛЯЕМЫХ ЭЛЕМЕНТОВ СРЕЗАЕМОГО СЛОЯ

3.1. ОСНОВНЫЕ ПРИНЦИПЫ ВЫДЕЛЕНИЯ ОТДЕЛЯЕМЫХ ЭЛЕМЕНТОВ СРЕЗАЕМОГО СЛОЯ

Эффективность работы режущего инструмента во многом определя-■ ется слоем металла, срезаемого при движении относительно обрабагы— ■.Баемого изделия. Приходящаяся на каждое режущее лезвие нагрузка определяется размерами отделяемых в процессе резания элементов срезаемого слоя. Форма и размеры таких элементов зависят от вида

I

режущего инструмента, его расположения и траектории перемещения в процессе резания.

быть соизмерен с длиной пути контакта режущей кромки инструмента с обрабатываемым изделием. Поперечное же сечение отделяемого эле­мента в процессе резания проектируется на переднюю поверхность ре­жущего клина инструмента и может быть определено по размеру об­разующего отпечатка или пятна контакта. Однако контролируемые с достаточной точностью размеры поперечных сечений отделяемых эле­ментов лучше задавать в конкретной секущей плоскости. Такой плос­костью может быть плоскость, перпендикулярная к вектору скорости резания W. Для простоты и удобства измерений она может быть заменена плоскостью, перпендикулярной к вектору скорости главного движения V.

3,2. СЕЧЕНИЯ ОТДЕЛЯЕМЫХ ЭЛЕМЕНТОВ СРЕЗАЕМОГО СЛОЯ ПРИ ОБРАБОТКЕ ЛЕЗВИЙНЫМИ ИНСТРУМЕНТАМИ

Анализ данных практики показывает, что поперечные сечения отде­ляемых элементов срезаемого слоя в подавляющем большинстве слу— чаев имеют форму прямоугольников и параллелограммов. Для опреде­ления площадей таких фигур достаточно знать размеры одной из сто­рон и высоту фигуры. Кроме того, сечение отделяемого элемента сре­заемого слоя всегда ограничено двумя соседними следами поверхнос­тей (или одной поверхности) резания. Поэтому для характеристики одной из сторон сечения используем размер, устанавливаемый вдоль следа поверхности резания (или с некоторым упрощением — вдоль главной режущей кромки). Назовем его шириной сечения отделяемого элемента (6, мм). Тогда высотой, или толщиной сечения отделяе­мого элемента (а, мм) будет являться размер, перпендикулярный к ширине.

Выделим эти размеры (геометрические параметры) на сечениях отделяемых элементов при продольном точении (рис. 3.1). Рассмот­рим два вида сечений А - А и Б - Б. Первое совпадает с плоскобтью, касательной к передней поверхности резца, второе — с плоскостью, перпендикулярной к вектору скорости главного движения V.

В (А — А) поперечное сечение отделяемого элемента образует фигуру ДВ DC • Здесь ВБ *" 6д - ширина отделяемого элемента, Яд-толщина. Подобным образом определяются эти параметры и в сечении

Б- Б (см. рис. 3.1), Здесь В^Ц- ву • В этом же сечении сторона JG фигуры AjB^BC является расстоянием между двумя соседними следами поверхности резания, измеряемым в направлении вектора подачи. Оно представляет собой путь, проходимый следом В.Б поверх­ности резания за время одного оборота детали или часть проекции вектора подачи на направление перемещения резца:

Скалярную величину размера Б С как часть проекции вектора подачи
найдем по зависимости '. _».

БС = А, В, = V₂₂₁ /и = ] Т₀ ] = S₀, (3.1)

где и. — частота вращения детали—изделия, об/мин.

Если считать, что основной стороной сечения отделяемого элемен­та является сторона Б С = $'_с, а не В,! "6^, то для определения площади сечения отделяемого элемента необходимо ввести дополни­тельно размер, перпендикулярный к Б С " 9<> • Таким дополнительным размером (см. рис. 3.1) является размер t. Назовем его глуби­ной резания. В ряде литературных источников под глубиной реэания понимается расстояние между обработанной и обрабатываемой поверх­ностями, измеренное по нормали к обработанной поверхности. Однако из—за трудностей, возникающих при установлении понятия обработан­ной поверхности, глубину резания проще задавать как размер сечения отделяемого элемента срезаемого слоя, устанавливаемый в направ­лении, перпендикулярном подаче.

Используем величины б, а, s и t для расчета объема и площа­ди сечения отделяемых элементов. Из рис. 3.1 имеем:

(3.2)

E₀.jV=a_ve_v.V,

где Е₀- объем отделяемого элемента срезаемого слоя (за одну мину­ту); t - площадь сечения отделяемого элемента (фигуры А. В. Б С),

Рис. Зл1; Схемы сечений срезаемого слоя

Z)

 

L ш x (³'³>

где a_/=S₀Sitt(f>, e_v=t/sinui (см. рис. 3.1); 1r *■ 3> Б rt /1000 м/мин.

Следует отметить, что с помощью параметров (a, в) можно устанавливать величину площади поперечного сечения отделяемого эле­мента в любой секущей плоскости, с помощью же параметров s₀,it. -только в сечении, перпендикулярном к вектору скорости главного дви­жения.

Рассмотрим ряд примеров.

3.2.1. Обработка резцами

В качестве примера рассмотрим сечения отделяемых элементов при токарной обработке (подрезке торца, отрезке, точении проходными резцами). На рис. 3.2 изображены сечения отделяемых элементов для названных случаев плоскостью,перпендикулярной к вектору скорости главного движения. При обработке отрезным резцом (рис. 3.2,6) се—

менная. Рассмотрим площади фигур А8СБ» A BE М и АДС II (рис.3.2,в). На основе принципа Кавальери получаем, что площади этих фигур рав­ны (так как размер любой из проведенных параллельно оси изделия линий равен s₀).

В самом общем случае при обработке резцами для определения площади сечения отделяемого элемента можно применять следующую зависимость:

i = s_ct=a_cpe, (3.4)

^гД^{е a}^„- среднее значение толщины сечения отделяемого элемента; 6 - полное значение ширины отделяемого элемента.

3.2.2. Сверление, зен кер ова н ие, развертывание

Форма сечений отделяемых элементов при обработке этими инстру­ментами приведена на рис. 3.3.

 

 

 

(1	№7.	ь
1i	I	It]

Рис, 3.2. Форма сечений отделяемых элементов срезаемого слоя при токарной обработке

чение отделяемого элемента имеет форму прямоугольника, при под­резке горца (рис. 3.2,а) - форму параллелограмма, при обработке радиусным резцом - серповидную форму (рис. 3.2,в). Во всех приве­денных случаях размер, устанавливаемый вдоль главной режущей кромки, является шириной сечения отделяемого элемента (ву), раз­мер же, измеренный по нормали к ширине, - -толщина этого сечения (ay). При обработке.резцом с криволинейной режущей кромкой (рис. 3.2,в) толщина сечения отделяемого элемента есть величина пере-

Рис. 3.3. Форма сечений отделяемых элементов срезаемого слоя при сверлении (а) и развертывании (зенкеровании) (б)

Для рассматриваемых случаев (исходя из условий образования от­деляемых элементов) необходимо иметь в виду, что сторона сечения отделяемого элемента S_ представляет собой скалярную величину час— ИИ проекции вектора подачи на направление осевого перемещения ин­струмента. Она устанавливается не за время одного оборота, как это было показано ранее для случая токарной обработки, а за время по­ворота инструмента на расстояние, равное одному угловому шагу между рабочими лезвиями инструмента.

Для этих случаев характерна следующая зависимость:

 

^v2xi^=sm*

Скалярное значение стороны сечения |s_z| получим следующим расче­
том: '.

⁸1 ⁼ *гм/**' (3.5)

где н, - частота вращения инструмента, об/мин; % - число зубьев инструмента,

В отличие от s_e, величина s. получила название "подачи на зуб". Для определения площади сечения элемента, отделяемого одним зу­бом, воспользуемся рис. 3.3, откуда имеем:

где a_L,,- толщина сечения элемента, отделяемого одним режущим

*(У) лезвием многозуб ого инструмента.

3.2.3. Фрезерование

А. Обработка цилиндрическими прямозубыми фрезами

Рассмотрим схему контакта цилиндрической фрезы с заготовкой изделия (рис. 3.4). Фреза совершает вращательное движение со ско­ростью 1г»_вхг, а заготовка - поступательное перемещение со скоро­стью 1г.ц,. Каждый зуб фрезы относительно заготовки проходит участ­ки равной длины, например, А Б, Б С и т.д. Удаляемый каждым зу­бом элемент срезаемого слоя имеет объем, равный произведению пло­щади фигуры А ЕС,В на высоту В. Длиной каждого отделяемого элемента, измеряемой в направлении вектора скорости резания, яв­ляется длина дуг АЕ, С Б и т.д. (дуг контакта зубьев фрезы с за­готовкой изделия).

Для определения размеров поперечного сечения отделяемого эле­мента необходимо рассмотреть его в плоскости, перпендикулярной к вектору скорости резания (W ** У_гвгг ^{+ v} 1аг)» ^{или для} просто­ты измерения - в плоскости, перпендикулярной к вектору скорости главного движения \Г = V_zezz. Для точки К, принятой на дуге кон­такта фрезы с заготовкой И С секущей плоскостью, перпендикуляр­ной к 1г, является плоскость А- А. В этой плоскости размер КК₍, измеренный вдоль следа поверхности резания, является шириной сече­ния отделяемого элемента 6_V, а размер И К — толщиной сечения

"■% IVM ** ^ач'К (где Ч* ~ угол, характеризующий расположение точ­ки К — на дуге Б С, для краткости - угол контакта^.

В го же время размер И, К,, измеренный между двумя соседни­ми поверхностями резания, равен скалярной величине части вектора подачи, так как последний направлен по радиусу фрезы для любой точки К., т.е.

И₁К₁ = ИК = а_2Су)к=а_ц/к = ₈'_гк.

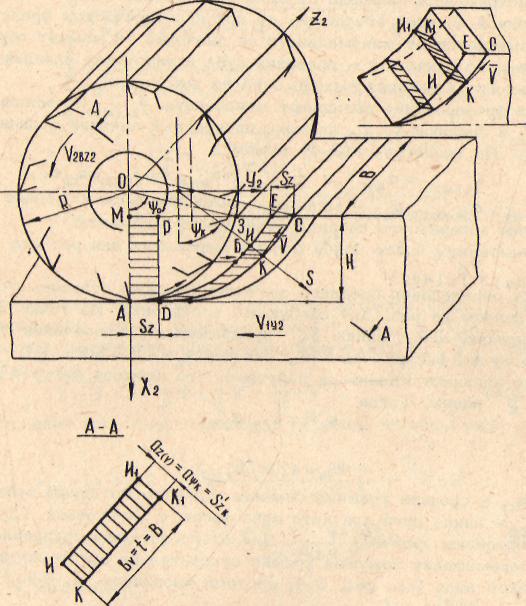
Рис. 3.4. Форма сечения отделяемых элементов срезаемого слоя'при фрезеровании цилиндрической фрезой с прямыми зубьями

Следует отметить, что для случая, когда точка К при своем п<=—
ремещении выходит на ось 0 9_г, значение подачи 8'_хк= И К стано­
вится равным 9_Ь s Е С (с^м- рис. 3.4), Для этих же условий спра­
ведлива следующая зависимость:

Глубина резания как размер, всегда перпендикулярный подаче, при цилиндрическом фрезеровании совпадает с шириной сечения отделяе­мого элемента e_v = t (см. рис. 3.4). Если у ранее рассмотрен­ных инструментов площадь сечения отделяемого элемента остается неизменной по всей его длине, то при цилиндрическом фрезеровании она изменяется от минимального ее значения (в момент образования отделяемого элемента — врезания зуба в заготовку изделия) до мак­симального (в момент выхода зуба из заготовки).

При фрезеровании различают мгновенную j.., максимальную j-. и среднюю^.. площади поперечных сечений отделяемых эле­ментов. По аналогии с (3.4) имеем:

ilCMJ") ^{= а}<¥* ⁸v'. fj(maxr^a4^,mor^evij^:zicpr^acp^eVi где а, а_ш __, а. •'— мгновенное, максимальное и среднее значения толщины поперечного сечения отделяемого элемента.

Попытаемся найти более полные выражения для расчета J_{b tc}„j,

НСтах) * J» (Mi) •

Для определения среднего значения толщины отделяемого элемента

а_ср сделаем на рис. 3.4 следующее построение. Из точки Л провег-дем прямую Б Р, линию 3 С продолжим до пересечения с осью фре­зы, Получим фигуру АБ Р М. Так как S_%s АБ я MP = Е С, то на основе принципа Кавальери получаем, что площади фигур AUPM и A3J С Е равны. Тогда

^sx^{H = l}C3)^acpi

или

%***Н/1_СВ, ⁽³-⁷⁾

где а_ср — средняя толщина сечения отделяемого одним зубом элемен­та; 1._- длина дуги контакта зуба фрезы с заготовкой, С Б = А Е.

Определим величину t--.. Для этого запишем уравнение траекто­рии перемещения режущей кромки относительно заготовки в парамет­рическом виде (см. рис. 3.4, система координат X _г О У ₂):

Х_г= R cos cut,,

где i> — скорость перемещения заготовки изделия, Ъ = 1г_1Ч„,мм/мин; t - промежуток времени, мин; ш - угловая скорость вращения фре­зы, град/мин; ш= 2.3iH (где к - частота вращения фрезы, об/мин); со t = Ц) - угол поворота фрезы, ip = %Ttnt.

Для определения 1._ используем известную зависимость

\.*Л- —гя.. (3.9)

Так жак X'a*₁₊wRcei«t У'—uftslH <ut» t

= SV4⁺ ^^coRcoswt + co²R¹' dt =

О

'^"'fW^F^ **■ ⁽³-^io)

Точное решение полученного интеграла затруднительно. Так как
Vu>R значительно меньше единицы (ъ,/шЦ. - 0,01...01) то по­
дынтегральное выражение можно представить как УГПГ и изло­
жить в ряд: '■' ^s ^^а-=>ло-

^Ч^К"^ (3.11)

Для решения воспользуемся двумя первыми членами ряда:

^{сл 1} XL (v, + coR)² J^aL-

Pound; -fc

(.1^ + U5R)2 <° L * Ctx1+coR)2 J =

. S J Or₁₊wR)*--------- ^dt

При t = Y„/<*> имеем:

О' О

О

⁼ to "~ tr, t oj R '

И ----- "------------------- tr, + coll ⁽³-¹²⁾

Для упрощения расчетов в качестве длины участка CD можно при­нять только первый член полученной разности:

V**"T1?------- — = *▼„+ Т1Г*о, (3.13)

S_e= V| / К г СО = Si3i»t.