Определим критические точки. Для этого приравняем вторую производную к нулю:
.
Это уравнение равносильно уравнению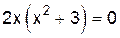 
, откуда 
.
Производная второго порядка не существует при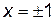 
. В итоге получили три критические точки: , 
, 
.
На числовой оси отложим все критические точки и определим знаки второй производной аналогично тому, как это сделано в пункте 7 (рис. 12):
,
,
 |
, 
.
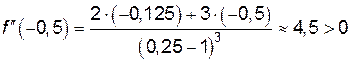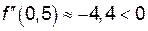При переходе через точку вторая производная меняет знак, следовательно, 
– точка перегиба графика функции. На интервалах 
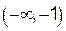и 
график функции является выпуклым, а на интервалах 
и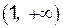 
– вогнутым. Составим таблицу исследования на выпуклость и вогнутость.
Таблица 5
| х | 
| -1 | 
| 
| 
| ||
| - | 
| + | - |
| + | |
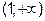
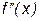
| выпуклый |
| вогнутый | выпуклый |
| вогнутый |
8) Вычислим значения функции в точках экстремума и перегиба:
, 
, 
.
Для более точного построения графика найдем значения функции в дополнительных точках: 
, 
.
Теперь построим график функции (рис. 13).
Пример 8.2. Исследовать методами дифференциального исчисления функцию 
и построить ее график.
Решение.
1) Исходя из того, что известны области определения элементарных функций 
и 
, получаем область определения функции: 
: 
.
2) Так как функция определена только для положительных значений 
, то она не является ни четной ни нечетной.
3) Найдем точки пересечения с осью 
: 
или 
, т. е. 
, откуда 
. Точки пересечения с осью 
не существует, так как 
никогда не обращается в нуль. Поэтому график функции пересекается с осями координат в единственной точке – 
.
4) Данная функция непрерывна на всей области определения.
Изучим поведение функции на левом конце области определения, для этого вычислим предел:
.
Отсюда прямая 
(ось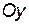 
) является вертикальной асимптотой к графику функции.
Найдем уравнения невертикальных асимптот. Для этого вычислим (используя правило Лопиталя) следующие пределы:
,
.
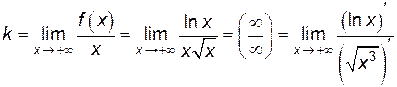
Полученная прямая (ось 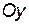) является горизонтальной асимптотой графика функции
5) Найдем 
:
.
Производная равна нулю, когда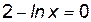 
, то есть при 
. Производная существует на всей области определения функции . Следовательно, существует только одна критическая точка.
Нанесем область определения и критическую точку на числовую ось и найдем знаки производной 
на всех интервалах (рис. 14):
, 
.
Так как при переходе через критическую точку производная меняет знак, то 
– точка экстремума функции (точка максимума). На интервале 
функция возрастает, а на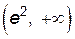 
– убывает.
6) Найдем 
:
.
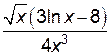Производная второго порядка равна нулю, если 
или 
, 
. Отсюда получаем: , 
. Так как не входит в область определения функции, то существует только одна критическая точка второго рода.
Нанесем область определения функции и критическую точку на числовую ось (рис. 15). Найдем знаки на всех полученных интервалах:
, 
. 
При переходе через критическую точку 
производная второго порядка сменила знак, следовательно, это точка перегиба графика функции. На интервале 
график является выпуклым, а на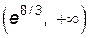 
– вогнутым.
7) Найдем значения функции при и 
:
, 
.
Для более точного построения графика вычислим значения функции 
в дополнительной точке: 
.
По полученным в пунктах 1–7 данным строим график функции 
(рис. 16).
Расчетно-графическое задание
Вариант 1
Задание 1. Вычислить производные заданных функций.
| 1. |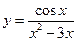 
| 5. | 
|
| 2. |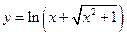 
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. | 
|
Задание 2. Логарифмическое дифференцирование. Дифференцирование неявной функции. Дифференцирование функции, заданной параметрически.
| 1. | 
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. | 
|
Задание 3. Найдите производную функции указанного порядка.
1) 
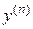, если 
; 2)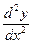 
, если 
.
Задание 4. Составить уравнение касательной, проведенной к кривой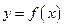 
, параллельно прямой 
.
.
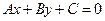Задание 5. Найти пределы функций, используя правило Лопиталя.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. | 
| 8. |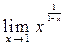 
|
Задание 6. Найти наименьшее и наибольшее значение функции в указанных промежутках.
Задание 7. Исследовать функции и построить их графики.
| 1. | 
| 2. | 
| 3. | 
|
Вариант 2
Задание 1. Вычислить производные заданных функций.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. | 
|
Задание 2. Логарифмическое дифференцирование. Дифференцирование неявной функции. Дифференцирование функции, заданной параметрически.
| 1. |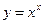 
| 4. | 
|
| 2. | 
| 5. |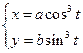 
|
| 3. |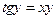 
|
Задание 3. Найдите производную функции указанного порядка.
1) 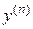, если 
; 2) 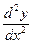, если 
.
Задание 4. Составить уравнение касательной, проведенной к кривой 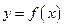, параллельно прямой .
.
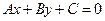Задание 5.Найти пределы функций, используя правило Лопиталя.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. |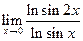 
| 8. | 
|
Задание 6. Найти наименьшее и наибольшее значение функции в указанных промежутках.
Задание 7. Исследовать функции и построить их графики.
| 1. | 
| 2. | 
| 3. |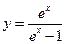 
|
Вариант 3
Задание 1. Вычислить производные заданных функций.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. | 
|
Задание 2. Дифференцирование неявной функции. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрически.
| 1. | 
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. | 
|
Задание 3. Найдите производную функции указанного порядка.
1) 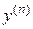, если 
; 2) 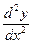, если 
,
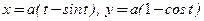Задание 4. Составить уравнение касательной, проведенной к кривой 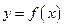, параллельно прямой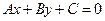
.
Задание 5. Найти пределы функций, используя правило Лопиталя.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. |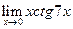 
| 7. |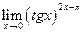 
|
| 4. | 
| 8. | 
|
Задание 6. Найти наименьшее и наибольшее значение функции в указанных промежутках.
Задание 7. Исследовать функции и построить их графики.
| 1. | 
| 2. | 
| 3. | 
|
Вариант 4
Задание 1. Вычислить производные заданных функций.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 
| 7. |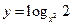 
|
| 4. | 
|
Задание 2. Дифференцирование неявной функции. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрически.
| 1. | 
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. |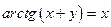 
|
Задание 3. Найдите производную функции указанного порядка.
1) 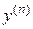, если 
; 2) 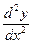, если 
,
Задание 4. Составить уравнение касательной, проведенной к кривой 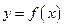, параллельно прямой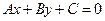
Задание 5. Найти пределы функций, используя правило Лопиталя.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. | 
| 8. |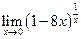 
|
Задание 6. Найти наименьшее и наибольшее значение функции в указанных промежутках.
