Найти 
.
Решение.
Пример 4.4. Найти 
, если переменные 
и 
связаны соотношением
.
Решение.
Явно выразить одну из переменных через другую невозможно, поэтому находим производные левой и правой частей данного равенства и приравниваем их:
.
Далее имеем:
;
.
Перенося слагаемые, содержащие , в одну часть равенства, вынося за скобку, а остальные слагаемые – в другую и деля на коэффициент при , получаем:
.
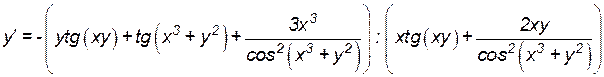Пример 4.5. Найти и 
для функции, заданной параметрически:
.
Решение
; 
;
;
;
;
.
4.4. Логарифмическое дифференцирование
Рассмотрим показательно-степенную функцию 
, где 
, u (x), v (x) – дифференцируемые функции.
Прологарифмируем равенство 
, получим: 
(по свойствам логарифмов). Дифференцируем обе части полученного равенства как неявную функцию, помня, что y – функция от x:
,
откуда 
.
Подставляя сюда 
, имеем:
.
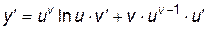Этот прием нахождения производной называется логарифмическим дифференцированием.
Пример 4.6. Найти 
.
Решение.
Вначале прологарифмируем данное равенство
,
и найдем производные от обеих частей полученного равенства, приравнивая их:
Учитывая, что 
, имеем:
.
Пример 4.7. 
, (x > 0). Найти производную функции y'.
Решение.
,
или 
.
5. Производные высших порядков
5.1. Понятие производной высшего порядка
Пусть функция 
определена и дифференцируема на некотором промежутке X, тогда ее производная 
также является функцией от x на этом промежутке. Если имеет производную на промежутке X, то эта производная называется производной второго порядка функции y = f (x) и обозначается: y'' или 
.
Итак, 
Производная от производной второго порядка называется производной третьего порядка и обозначается: y''' или 
.
Вообще, производной n-го порядка называется производная от производной 
-го порядка и обозначается: y (n) или f (n)(x). Итак,
f (n)(x) = (f (n -1)(x)) '.
Производные y'', y''',... называются производными высших порядков.
Пример 5.1. 
. Найти 
и 
.
Решение.
= 
= 
,
= – 
,
= 
= 
,
= 
= 
= 
.
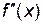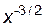Пример 5.2. Найти производную n -го порядка для функции 
.
Решение.
,
,
.
По аналогии находим: 
.
5.2. Производные высших порядков от функций,
заданных параметрически
Пусть функция y, зависящая от x, задана параметрически на интервале Т:
, 
Найдем . Известно, что = = 
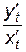(п. 4.3), поэтому
= 
= 
= 
= 
.
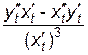Аналогично будет вычисляться 
и т. д.
Пример 5.3. Найти 
и 
для функции, заданной параметрически:
.
Решение.
;
;
;
;
;
=
.
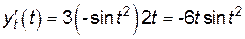Пример 5.4. Функция y от x задана параметрически уравнениями:
, 
.
Найти .
Решение.
= = = 
= 
;
= = 
=- 
= 
.
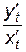5.3. Производные высших порядков от функций,
заданных неявно
Нахождение производных высших порядков от функций, заданных неявно, рассмотрим на примере.
Пример 5. 5. Найти , для функции, заданной неявно уравнением: 
. Вычислить y' (0), y'' (0).
Решение.
Найдем сначала y', как описано в п.4.2.
,
,
,
= 
.
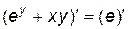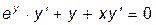Для нахождения y'' будем дифференцировать равенство 
, получим:
.
Отсюда найдем y'' и подставим найденное выражение для y': 
,
y'' =– 
= 
= 
=
= 
.
Итак, y' =–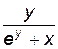 
,
y'' = .
Подставим x=0 в исходное уравнение , получим:
, откуда y =1, значит,
y (0)=1; y' (0)=– 
; y'' (0)= 
= 
.
6. Правило Лопиталя
Рассмотрим новый способ нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, т.е. раскрытия неопределенностей типа 
и 
, так называемое правило Лопиталя.
Теорема Лопиталя 1 (раскрытие неопределенностей типа ). Пусть функции 
, 
определены, непрерывны и дифференцируемы в точке x 0 и некоторой ее окрестности, причем 
для любого x из этой окрестности, и пусть 
, 
(следовательно, , – бесконечно малые при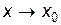 
). Если 
существует, то существует 
и
= . (6.1)
Пример 6.1. Найти 
.
Решение.
Так как при 
функции 
и 
, то имеем неопределенность типа . Числитель и знаменатель данной дроби непрерывны дифференцируемы и стремятся к нулю. Это означает, что можно применить правило Лопиталя:
.
Пример 6.2. Найти 
.
Решение.
Поскольку функции 
, g(x)=2x удовлетворяют условиям теоремы Лопиталя, то = 
=0.
Замечание 1. Теорема Лопиталя справедлива и в том случае, когда функции , не определены в точке x0, но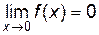 
и 
.
В самом деле, если доопределить , , положив 
, тогда , будут непрерывны в точке x 0, а потому теорема Лопиталя будет применима к ним.
Замечание 2. Правило Лопиталя применимо и в том случае, когда
, 
.
Действительно, введя новую переменную 
, видим, что y→ 0 при x →¥. Тогда 
= 
= 
= 
.
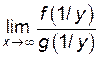Теорема Лопиталя (раскрытие неопределенностей типа 
).
Пусть функции , дифференцируемы в окрестности точке x 0, за исключением самой точки x 0, причем , и пусть 
, 
. Если существует 
то существует и 
, причем
= 
.
Замечание 3. Предел отношения двух функций может существовать, в то время как предел отношения их производных не существует.
Например, 
=1, а 
= 
– не существует, так как 
не существует.
Пример 6.3. Найти 
.
Решение.
При x → 0 и x > 0 
, 
, следовательно, имеем отношение двух бесконечно больших при x →0 и неопределенность типа 
. Вычислим:
= – 
= – 
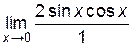= 0.
Пример 6.4. Найти 
.
Решение.
Замечание 4. Если 
при x → x 0 (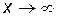
) является неопределенностью типа или 
, и , g' (x) удовлетворяют условиям теоремы Лопиталя, то
= = 
.
Таким образом, для раскрытия неопределенностей типа или иногда приходится применять правило Лопиталя несколько раз.
Замечание 5. Теорема Лопиталя остается верной и тогда, когда = 
.
Пример 6.5. Найти 
.
Решение.
Имеем неопределенность типа . Применяя теорему Лопиталя два раза, получим: 
= 
= 
=¥.
Пример 6.6. Найти 
.
Решение.
Так как 
, то имеем неопределенность типа (0·¥). Преобразуем ее к виду :
= 
, затем применим правило Лопиталя:
= 
= 
= 
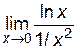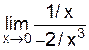=0.
Итак, 
.
Пример 6.7. Найти 
Решение.
.
Пример 6.8. Найти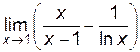 
.
Решение.
.
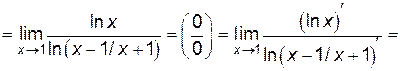
Пример 6.9. Найти 
.
Решение.
В данном случае имеем неопределенность типа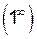 
, поэтому для раскрытия этой неопределенности применим метод логарифмирования.
