Пусть 
. Тогда с учетом того, что логарифмическая функция непрерывна, имеем 
Так как 
, то 
.
7. применение производной для
исследования свойств функций.
7.1. Возрастание и убывание функций
Функция 
называется возрастающей (убывающей) на некотором интервале 
, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции, т. е. при 
выполняется неравенство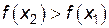 
.
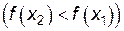Интервалы, в которых функция возрастает или убывает, называются интервалами монотонности функции.
Рассмотрим применение производной для нахождения интервалов монотонности функций.
Теорема 1 (достаточное условие возрастания функции). Если функция непрерывна на отрезке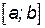 
и дифференцируема на интервале , причем 
(
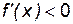) для любого 
, то эта функция возрастает (убывает) на отрезке .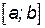
Пример 7.1. Исследовать на монотонность (т. е. возрастание и убывание) функцию: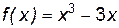 
Решение.
.
Неравенство , т. е. 
, справедливо для x <–1 и для x >1. Следовательно, функция 
возрастает на интервалах (–¥, –1)
и (1, +¥).
Поскольку неравенство 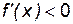, т. е. 
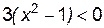справедливо для
x Î (–1, 1), то на интервале (–1, 1) функция убывает.
7.2. Экстремумы функции
Дадим точные определения точкам максимума и минимума функции. Пусть функция определена на промежутке X и x0 Î X. Говорят, что в точке x0 функция имеет максимум (минимум), если существует такая окрестность точки x 0, что для любого x из этой окрестности 
(
).
Точки максимума и минимума называются точками экстремума.
Замечание 1. Точки экстремума всегда являются внутренними точками промежутка, т. е. не могут быть его концом.
Теорема 2 (необходимое условие экстремума). Если функция дифференцируема в точке x 0 и некоторой ее окрестности и x 0 – точка экстремума, то 
.
Следствие. Если x 0 – точка экстремума, то или 
не существует.
В качестве примера приведем функцию 
(рис. 3).
|
Очевидно, что x 0 = 0 является точкой минимума, так как |0|<|x| для любого x ≠ 0. А в точке x 0 = 0 производной 
не существует.
Если или f' (x 0) не существует, то точку x 0 будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.
Теорема 3 (первое достаточное условие экстремума). Пусть функция 
определена и непрерывна в точке x 0 и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, быть может самой точки x 0, и точка x 0 – критическая точка для функции (т. е. 
или не существует). Тогда:
1) если при x < x 0 производная , а для x > x 0: 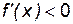, то x 0 – точка максимума;
2) если при x < x 0: 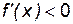, а при x > x 0: , то x 0 – точка минимума.
Пример 7.2. Исследовать на монотонность и экстремумы функцию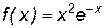 
. Построить её график.
Решение.
Заданная функция определена и непрерывна на всей числовой оси 
. Найдем производную: 
.
Тогда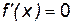 
при x 1=0 и x 2 =2. Точки x 1, x 2 – критические точки. Эти точки разбивают всю числовую ось на три интервала: (–¥; 0), (0; 2),
(2; +¥). Составим таблицу, в первой строке которой поместим указанные точки и интервалы, во второй строчке – сведения о производной 
в точках и на интервалах, а в третьей – поведение данной функции (табл. 2).
Таблица 2
| x |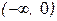 
| (0, 2 ) | 
| ||
| 
| 
|
| ||
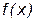
| убывает |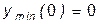 
| возрастает |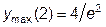 
| убывает |
Определим знак на каждом из интервалов: если x Î (–¥, 0), то 
; если xÎ(0, 2), то ; если x Î(2, +¥ ¥), то 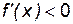. Отсюда определяется поведение функции : на первом и последнем интервалах функция убывает, а на втором – возрастает (рис.4).
|
Рис. 4
Отсюда следует, что x 1 = 0 является точкой минимума, 
,
а x 2 =2 – точка максимума, 
.
7.3. Наибольшее и наименьшее значения функции на отрезке
Известно, что если функция непрерывна на отрезке, то она достигает на этом отрезке своего наименьшего и наибольшего значения. Иногда требуется найти наименьшее или наибольшее значение такой функции.
Если на отрезке 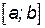есть точки минимума и максимума функции , то наименьшее значение функция будет принимать либо в одной из точек минимума, либо на конце отрезка 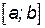. Аналогично для наибольшего значения.
Сформулируем алгоритм нахождения наибольшего и наименьшего значения функции f (x), непрерывной на отрезке:
1. Найти критические точки x 1, x 2,..., xn функции . Для этого необходимо решить уравнение 
.
2. Отобрать все критические точки, принадлежащие отрезку .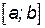
3. Вычислить значения функции в этих критических точках и на концах отрезка.
4. Из этих значений выбрать самое большое и самое малое. Эти числа и будут наибольшим и наименьшим значениями на отрезке .
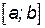Пример 7.3. Найти наименьшее и наибольшее значения функции
Решение.
1. Найдем критические точки для данной функции:
;
при x1=0, x2 =– 1, x3 = +1.
2. Все три критические точки принадлежат данному отрезку.
3. Вычислим значения функции в точках: 
:
4. Из найденных значений самое малое число 4, а самое большое число 13.
Таким образом, наименьшее значение функции равно 4, в точке х = 1, наибольшее значение равно 13, в точке х = 2 и в точке х = -2.
Пример 7.4. Найти наибольшее и наименьшее значения функции
на отрезке 
.
Решение.
1. 
, 
определена во всех точках; 
при 
.
2. На отрезке , при 
.
3. Имеем три точки: 
, 
, 
, в которых может достигаться наибольшее и наименьшее значения.
;
;
.
Итак, 
, 
.
Пример 7.5. Найти наибольшее и наименьшее значения функции
на отрезке 
.
Решение.
1. Найдем критические точки функции из условия, что 
или такие, при которых 
не существует:
.
Производная во всех точках существует, , когда 
.
Раскладывая левую часть на множители, получаем:
.
Отсюда находим критические точки: 
, 
, 
.
2. Из этих точек отрезку 
принадлежат только две: и .
3. Найдем значения функции в этих точках и на концах отрезка, т. е. при 
, 
, 
, 
:
;
;
= 
;
.
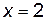Итак, получили 
, 
.
Среди многих применений производной функции одной переменной важное значение имеет решение так называемых задач на максимум (минимум).
Пример 7.6. Найти прямоугольный треугольник наибольшей площади, у которого сумма катета и гипотенузы равна 
.
Решение.
Обозначим один из катетов треугольника через 
, тогда гипотенуза будет равна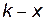 
, а другой катет, по теореме Пифагора будет равен:
.
Площадь треугольника 
, так как 
должна быть максимальной, то 
или 
не существует. Находим производную:
.
не существует, если 
, но тогда катет окажется равным гипотенузе, что невозможно. 
, если 
. Тогда 
.
Проверяем является ли эта точка точкой максимума. При 
, а при 
. Таким образом при площадь треугольника будет наибольшей.
Гипотенуза будет равна 
, т. е. 
, где
– угол, прилежащий к катету . Значит, 
; другой угол будет 
.
Следовательно, искомый треугольник – это прямоугольный треугольник с углами 
и сторонами 
, 
и 
.
Пример 7.7. Из трех одинаковых досок изготовить симметричный желоб с наибольшей площадью поперечного сечения.
Решение.
Ширину данных досок обозначим через 
. Поперечное сечение желоба изображено на рис. 5,.
Обозначим через угол 
(
), тогда 
, 
.
Площадь поперечного сечения (площадь трапеции) будет:
.
Наибольшее значение эта функция принимает в точке максимума, а необходимым условием того, что точка является точкой максимума функции 
, является то, что или не существует. Найдем :
.
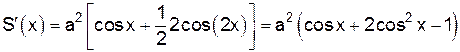Но 
всегда существует. Точки, в которых , находятся из уравнения: 
. Тогда 
или . Если , то 
.
Но в этом случае никакого желоба не получится, так как . Остается случай, когда, , тогда , так как 
.
Проверим, является ли эта точка точкой максимума функци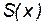и 
. При 
, производная функции принимает положительные значения, а при 
- отрицательные. То есть при площадь поперечного сечения желоба будет наибольшей.
Таким образом, действительно точка максимума. А площадь поперечного сечения составит
.
7.4. Выпуклость, вогнутость графика функции, точки перегиба
Пусть – функция, дифференцируемая на интервале 
. Рассмотрим кривую, являющуюся графиком функции 
.
Кривая, заданная функцией , называется выпуклой на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая называется вогнутой на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале.
Точка кривой M 0(x 0, f (x 0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Теорема 4 (достаточные условия выпуклости и вогнутости графика функции). Если во всех точках интервала вторая производная функции отрицательна, т. е. 
, то кривая на этом интервале выпукла; если во всех точках интервала – 
, то кривая на этом интервале вогнута.
Пример 7.8. Определитьнаправление выпуклости и точки перегиба кривой 
Решение.
Ищем точки х из области определения функции, в которых 
или не существует.
Вторая производная равна нулю в точках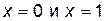 
. Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как 
существует всюду.
