Сообщение темы и целей урока. Изучение нового материала.

Изучение нового материала.

Задания 1,2, 7, 4, 3, 5*

Знакомство с уравнением можно начать с рассмот­рения уже известных равенств с пустым «окошком»:

+2 = 5.

Какое число надо подставить в «окошко», чтобы ра­венство было верным? (3.) Как вы это нашли? (5 — это и 3.) Неизвестное число обозначим цифрой х (икс) и получим запись: х + 2 = 5. Это уравнение. Читается так: икс плюс 2 равно 5. Решить уравнение — это зна­чит найти неизвестное число х. Показывается способ решения уравнения, основанный на связи между ком­понентами действия сложения. Первое слагаемое — х, в торое слагаемое — 2, сумма — 5. Какой компонент неизвестный? Как его найти? (Из суммы надо вычесть и местное слагаемое: х = 5 - 2, х = 3.) Сделаем проверку: 3 + 2 = 5, 5 = 5.

Учитель знакомит с образцом оформления решения уравнения. Потом ученики под руководством учителя закрепляют способ решения простейших уравнений, выполняя задание 1 из учебника.

Задание 1. Каждое уравнение ученики читают и комментируют решение. Записи решений оформляют по образцу.

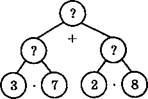
Задание 2.

По 3 кн. — 7 уч.

По 2 кн. — 8 уч.?

Решение задачи записыва­ется на доске и в тетради.

Задание 3.

Д. — 12 см

Ш. —?, в 4 раза меньше

Периметр —? см

Как получить отрезок, длина которого в 4 раза меньше длины прямоугольника? (Надо длину прямо­угольника разделить на 4.) Чему равна ширина пря­моугольника?

12:4 = 3 (см)

Найдите его периметр разными способами.

Задание 4.

1 + 9 < 20 — правильно; 17 + 9 < 20 — неправильно;

4 + 9 < 20 — правильно; 19 + 9 < 20 — неправильно.

16 + 9 < 20 — неправильно. Ответ: 1, 4.

 

Закрепление изученного материала.

Задание 5*.

 

Сколько марок у Максима и Глеба вместе? (27 ма­рок.) У кого марок меньше? (У Глеба.) Обозначим мар­ки Глеба отрезком. У кого марок больше? (У Макси­ма.) Во сколько раз? (В 2 раза.) Что это значит? (У него столько же марок, сколько у Глеба, и еще столько же.) Сколько раз надо взять марки Глеба, чтобы получить такое же количество, как у Максима? (2 раза.) Сколько раз надо взять марки Глеба, чтобы получить 27 марок? (3 раза.) Как узнать, сколько у Глеба марок?

 

 

27: 3 = 9 (м.)

Сколько марок у Максима?

9•2 = 18 (м.)

Значит, у Глеба 3 набора по 3 марки, остальные марки у Максима. Всего 4 набора, или 18 марок.

5•3+3•1 = 18 (м.)

Подведение итогов урока.

Домашнее задание

№ 9, 10, с.41.

 

Тема урока: Уравнение

Цели урока: 1) научить учеников решать про­стейшие уравнения, у которых неизвестный множи­тель, делимое, делитель;

2) решать текстовые задачи;

3) воспитывать любознательность, усидчивость.

Ход урока

Организационный момент.

Проверка домашнего задания.

3. Устный счёт.

Задания 4, 8.(устно)

Сообщение темы и целей урока.

Изучение нового материала.

Задания 1,5, 7, 3, 2, 6*.

Задание 3.

Кл. — 20 т.?

Лин. —?, в 2 р. меньше

Способ I.

20 + 20: 2 = 30 (т.)

Способ II.

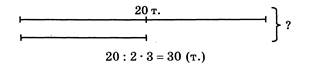
Задание 5. 4-9 + 17 = 36 + 17 = 53;

20 + 20:4 = 20 + 5 = 25.

Задание 6*. Запишем начальное положение: 10, 0, 0. В первом ведре — 10 л воды. Во второе ведро можно налить 7 л, поскольку оно пустое; в третье вед­ро можно налить 3 л. Будем переливать воду из пер­вого ведра в другие и записывать результаты. (10, 0, 0) — (3, 7, 0)— (3, 4, 3)— (6, 4, 0)—(6, 1, 3)—(9, 1, 0)—(9, 0, 1)-(2, 7, 1) —(2, 5, 3)