Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.
Для решения задачи:
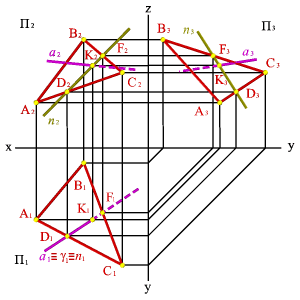
1. Через горизонтальную проекцию прямой а 1 проведем вспомогательную горизонтально проецирующую плоскость g (таким образом а g Î).
2. Горизонтальный след плоскости g1 пересекает проекцию плоскости A 1 В 1 С 1 в точках D 1 и F 1, которые определяют положение горизонтальной проекции п 1 - линии пересечения плоскостей g и AВС. Для нахождения фронтальной и профильной проекции п спроецируем точки D и F на фронтальную и профильную плоскости проекций.
3. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает проекции а в точке К, которая и является проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К 1.
4. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.

| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 5.21. Нахождение точки пересечения прямой и плоскости | |||
Таким образом алгоритм решения задачи состоит из следующей последовательности действий (рис.5.21):
1. Построение вспомогательной секущей плоскости g ( горизонтально – проецирующая плоскость ), которую проводят через прямую а (а)gÎ;
2. Построение линии пересечения вспомогательной плоскости g и заданной плоскости a (п)gÇa=;
3. Определение искомой точки К, как точки пересечения двух прямых, заданной - а и полученной в результате пересечения плоскостей – п (К = а Ç п). В качестве вспомогательной плоскости g рекомендуется брать одну из проецирующих плоскостей.
4. Определение видимости прямой а относительно плоскости a.
| Прямая линия перпендикулярная плоскости. |
Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.
Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n 1 ^h1. Аналогично для фронтали – f ^ n Þ f2 ^ n 2.
Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.
Доказательство следует из теоремы о проецировании прямого угла.
Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.5.22).






