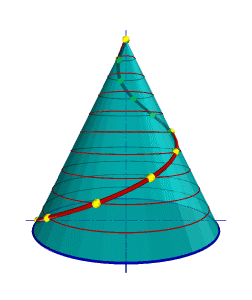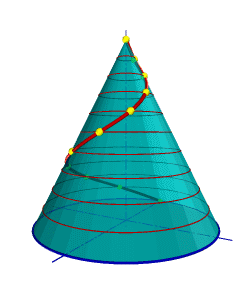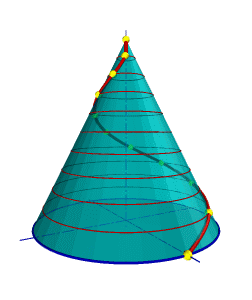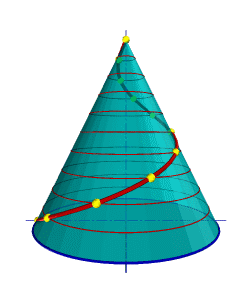
Такую линию описывает точка, которая движется по какой-либо образующей прямого кругового конуса, вращающегося вокруг своей оси так, что путь пройденный точкой по образующей все время равен углу поворота конуса (рис.7.10).
| Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда - одна из замечательных плоских кривых линий. | 
| |
| ||
| а) модель | б) эпюр | |
| Рисунок 7.10 Коническая винтовая линия |
Лекция №8 часть 1
Поверхность. Формообразование поверхностей. Поверхности вращения. Винтовые поверхности. Линейчатые поверхности с плоскостью параллелизма (Поверхности Каталана). Поверхности параллельного переноса.
| Поверхность |
" Поверхность, одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.
1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых П. определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, поверхность шара - множество точек, отстоящих на заданном расстоянии от данной точки. Понятие "Поверхность" лишь поясняется, а не определяется. Например, говорят, что поверхность есть граница тела или след движущейся линии.
2) Математически строгое определение поверхности основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям)...."
*Большая советская энциклопедия.
Поверхности составляют широкое многообразие нелинейных фигур трехмерного пространства. Инженерная деятельность человека связана непосредственно с конструированием, расчетом и, изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации конструирования, расчета и воспроизведения сложных технических поверхностей. Способы формообразования и отображения поверхностей, начертательной геометрии составляют основу инструментальной базы трехмерного моделирования современных графических редакторов.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z) - многочлен n-ой степени) и трансцендентные (F(x,y,z) - трансцендентная функция).
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
В начертательной геометрии фигуры задаются графически, поэтому целесообразно поверхность рассматривать как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии.
| образование и задание поверхности на чертеже. |
Поверхность можно рассматривать, как совокупность последовательных положений l 1, l 2 … линии l, перемещающейся в пространстве по определенному закону (рис.8.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму - изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в одной линии или целого семейства линий (m, n, p...). Подвижную линию принято называть образующей, неподвижные - направляющими. Такой способ образования поверхности принято называть кинематическим.
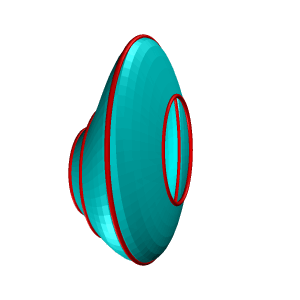
| Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество, линий конгруэнтных профилю резца. По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая. Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся. Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Это так называемые циклические поверхности (рис.8.2). Если же группировать поверхности по закону движения образующей линии и производящей поверхности, то большинство встречающихся в технике поверхностей можно разделить на: ·Поверхности вращения; ·Винтовые поверхности; ·Поверхности с плоскостью параллелизма; ·Поверхности переноса. Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают ее форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов). Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности. Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом. Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже. Различают две части определителя: геометрическую и алгоритмическую. Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности. Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу. Например, циклическая поверхность, каркас которой состоит из окружностей (рис.8.3), может быть задан следующим образом: ·Геометрическая часть определителя: три направляющих l, m, n, ось i пучка плоскостей ·Алгоритмическая часть: выделяем из пучка плоскостей с осью i плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим окружность, определяемую тремя найденными точками. Переходим к следующей плоскости пучка и повторяем построение. |
| Рисунок 8.1. Поверхность образованная движением линии | |
| |
| Рисунок 8.2. Циклическая поверхность | |
Рисунок 8.3. Образование циклической поверхности
|
| Поверхности вращения. |
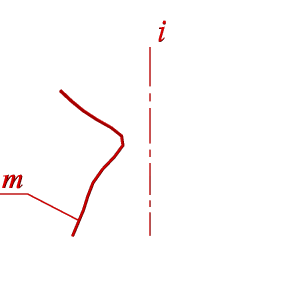
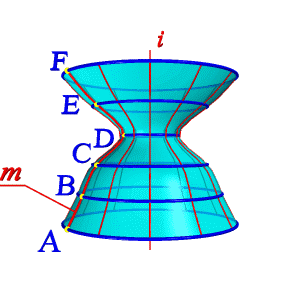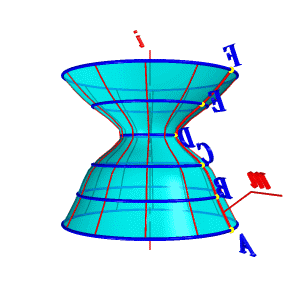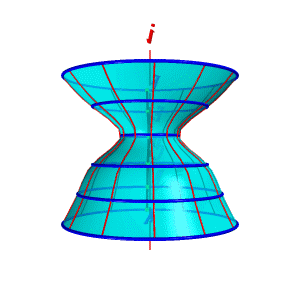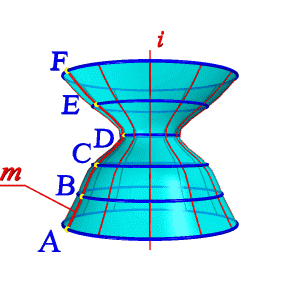
Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i (рис.8.4).
Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис 8.4.а).
Алгоритмическая часть включает две операции:
1. На образующей m выделяют ряд точек A, B, C,… F;
2. Каждую точку вращают вокруг оси i.
| 
| |
| а) эпюр | 
| б) модель |
| Рисунок 8.4. Образование поверхности вращения | ||
| Так создается каркас поверхности, состоящей из множества окружностей (рис.8.5), плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. 2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам. Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом. |
| Рисунок 8.5 Поверхность вращения |
| 
| |
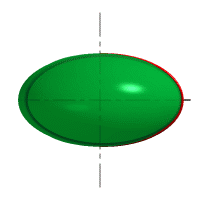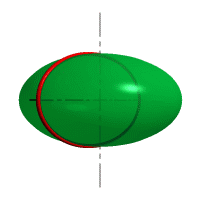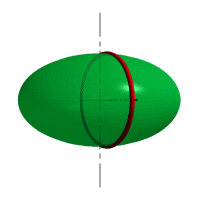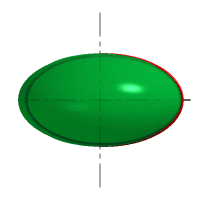
| Рисунок 8.6. Образование сферы | Рисунок 8.7. Образование сфероида | |
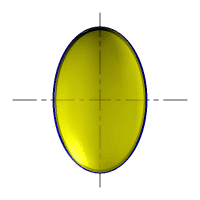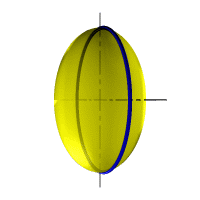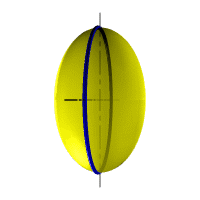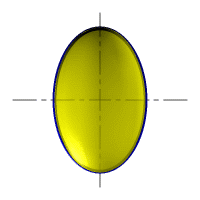
| Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими: Сфера – образуется вращением окружности вокруг её диаметра (рис.8.6). При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг большой оси то эллипсоид называется вытянутым (рис.8.8), если вокруг малой – сжатым или сфероидом (рис.8.7). Тор – поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.8.9). Параболоид вращения – образуется при вращении параболы вокруг своей оси (рис.8.10). |
| Рисунок 8.8. Образование вытянутого эллипсоида |
| 
|
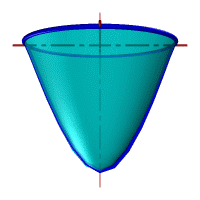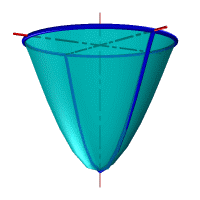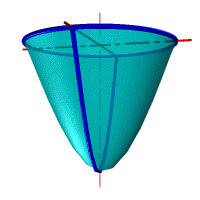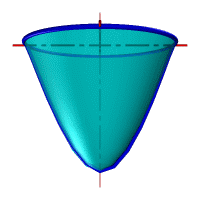
| Рисунок 8.8. Тор | Рисунок 8.10. Параболоид вращения |
| 
|
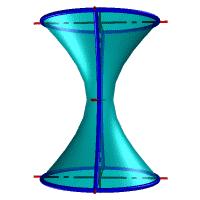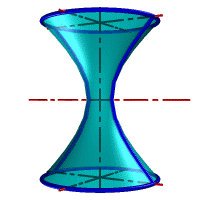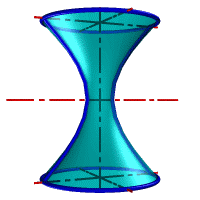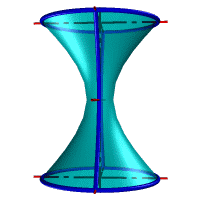
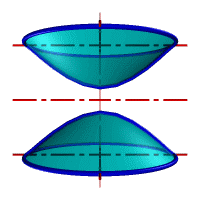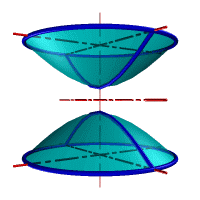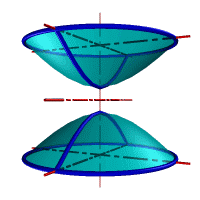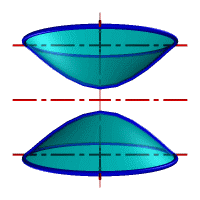
| а) однополостной | б) двуполостной |
| Рисунок 8.11. Гиперболоид вращения |
Гиперболоид вращения – различают одно (рис.8.11а) и двух (рис.8.11б) полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.
| Винтовые поверхности. |
Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.
| При этом поступательное и угловое перемещение находятся в определенной зависимости ∆h=k∆v, где ∆h – линейное перемещение за время ∆t, ∆v– угловое перемещение за то же время, k – коэффициент пропорциональности. Если k=Const, то шаг поверхности постоянный. Геометрическая часть определителя винтовой поверхности ни чем не отличается от поверхности вращения и состоит из двух линий: образующей m, и оси i(рис.8.12). Алгоритмическая часть: 1. На образующей m выделяют ряд точек А, В, С, … 2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки. | |
| Рисунок 8.12. Винтовая поверхность | ||
| Линейчатые поверхности с плоскостью параллелизма (поверхности каталана). |
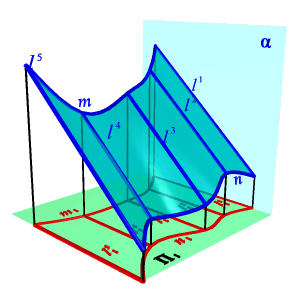
| Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n (рис. 8.13). В зависимости от формы направляющих образуются три частных вида поверхностей. Цилиндроид. Цилиндроидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим кривым линиям, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.13). Коноид. Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых кривая линия, а другая прямая, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.14). |
| Рисунок 8.13. Цилиндроид |
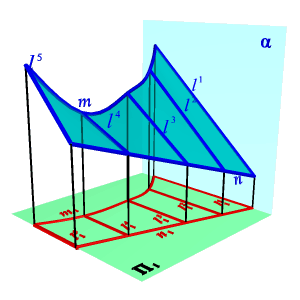
Гиперболический параболоид. Гиперболическим параболоидом или косой плоскостью называется поверхность, образованная движением прямолинейной образующей, параллельной плоскости параллелизма, по двум направляющим линиям – скрещивающимся прямым (рис.8.15).
| 
|
| Рисунок 8.14. Коноид | Рисунок. 8.15. Гиперболический параболоид |
| Поверхности параллельного переноса. |
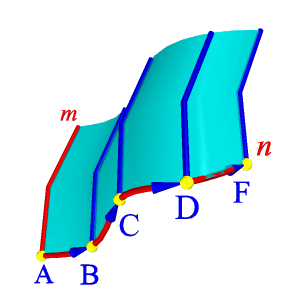
| Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии m по криволинейной направляющей n (рис.8.16). Геометрическая часть определителя состоит из двух кривых линий образующей - m и направляющей – n. Алгоритмическая часть определителя содержит перечень операций: 1. На направляющей п выбираем ряд точек А, В, С,… 2. Строим векторы АВ, ВС,… 3. Осуществляем параллельный перенос линии т по векторам АВ, ВС, … Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве. | |
| Рисунок 8.16. Поверхность параллельного переноса | ||
Лекция №8 часть 2
Линия и точка, принадлежащие поверхности. Пересечение поверхности плоскостью. Конические сечения.
| Линия и точка, принадлежащие поверхности |
Для определения принадлежности точки и линии поверхности рассмотрим следующие позиционные задачи:
Задача 1. Построение линии принадлежащей поверхности, если одна из проекций линии задана (рис. 8.17).
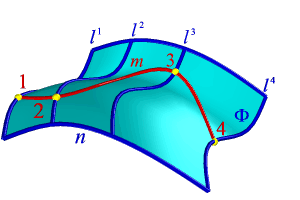
| Дано: 1.Поверхность Ф, заданная проекциями каркаса состоящих из образующих линий l и направляющей n. 2. Проекция линии m 2,принадлежащей поверхности Ф. |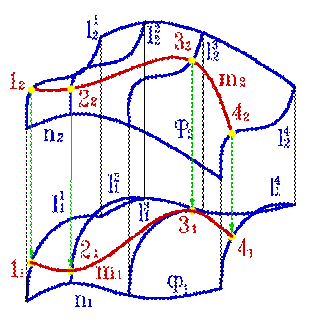 
| |
| ||
| а) модель | б) эпюр | |
| Рисунок 8.17. Линия на поверхности |
Алгоритм решения задачи:
1. Находим точки 1 2, 2 2, 3 2 , 4 2 пересечения проекции линии m2 с проекцией каркаса поверхности, т.е. соответственно с проекциями линий l 12, l 22, l 32, l 42.
2. По линиям связи находим проекции точек 1 1, 2 1, 3 1, 4 1, как точки лежащие на проекциях образующих каркаса соответственно l 11, l 21, l 31, l 41 и определяющих положение проекции линии т1 на поверхности Ф.
Задача 2. По одной проекции точки, принадлежащей поверхности, найти точку на поверхности (рис. 8.18).
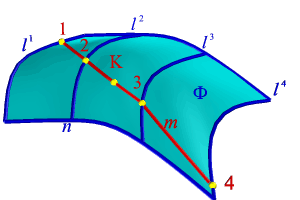
| Дано: 1. Поверхность Ф, заданная проекциями каркаса состоящего из образующих l и направляющих n. 2. Проекция точки К 1,принадлежащей поверхности Ф. |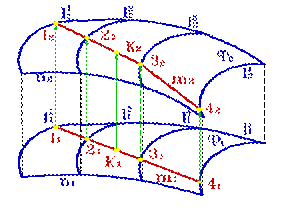 
| |
| ||
| а) модель | б) эпюр | |
| Рисунок 8.18. Точка на поверхности |
Алгоритм решения задачи:
1. Через заданную проекцию точки К 1 проводим одноименную проекцию произвольной вспомогательной линии принадлежащей поверхности т 1.
2. Находим точки 1 1, 2 1, 3 1, 4 1, пересечения проекции линии m 1 с проекцией каркаса поверхности, т.е. соответственно с проекциями линий l 11, l 21, l 31, l 41.
3. По линиям связи находим проекции точек 1 2, 2 2, 3 2, 4 2 как точки лежащие на проекциях образующих каркаса соответственно l 12, l 22, l 32, l 42 и определяющих положение проекции линии т 2 на поверхности Ф.
4. По линии связи находим положение проекции точки К 2, как точку принадлежащую вспомогательной линии т 2.
| Пересечение поверхности плоскостью |
В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая. Рассмотрим решение задачи по определению линии пересечения сферы фронтально - проецирующей плоскостью α (рис.8.19).
| 
| |
| а) модель | б) эпюр | |
| Рисунок 8.19. Пересечение сферы фронтально - проецирующей плоскостью |
Окружность, по которой плоскость α пересекает сферу, проецируется на плоскости П 1 и П 3 в виде эллипса, а на плоскость П 2 в прямую линию ограниченную очерком сферы.
Охарактеризуем выбранные для построения точки:
·1, 8- две вершины эллипса, определяющие положение малой оси, их фронтальные проекции определяют пересечение следа плоскости α с очерком сферы, а горизонтальные проекции являются соответственно высшей и низшей точками сечения
·2, 3- фронтальные проекции этих точек лежит на вертикальной оси сферы, а профильные проекции будут лежать на очерке сферы и определять зону видимости при построении эллипса на П 3.
· 4, 5- две вершины эллипса, определяющие положение большой оси эллипса, положение их фронтальной проекции определяет перпендикуляр, опущенный из центра сферы к следу плоскости α.
· 6, 7- Фронтальные проекции этих точек лежат на горизонтальной оси сферы, т.е. принадлежат экватору сферы, их горизонтальная проекция лежит на очерке сферы и определяет зону видимости при построении эллипса на П 1.
Линия пересечения плоскости α и сферы на фронтальной плоскости проекций совпадает со следом плоскости на ней отмечаем точки 1 2… 8 2. Для нахождения горизонтальных проекций этих точек в общем случае используется метод вспомогательных секущих плоскостей (β - горизонтальные плоскости уровня). Например, через точки 2 2, 3 2 проведем след плоскости β 12, на горизонтальной плоскости проекций линией пересечения плоскости β 1 и сферы будет окружность m 11, а точки 2 1 и 3 1 лежат на этой окружности по линии связи (в данном случае осевой линии). Таким образом находятся все точки, кроме 1 1 и 8 1, которые ввиду своего положения на очерке фронтальной проекции сферы будут принадлежать горизонтальной осевой линии на плоскости П 1. Построенные точки 1 1… 8 1 соединим плавной кривой линией с учетом видимости.
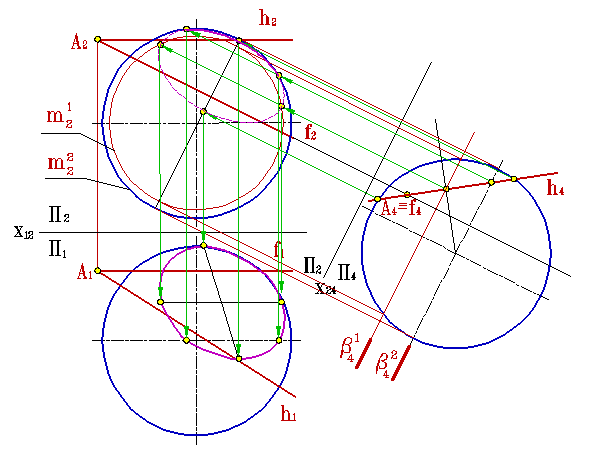
Задача, когда сферу пересекает плоскость общего положения, например заданная двумя пересекающимися прямыми α (h∩f) решается следующим образом:
| |
| Рисунок 8.20. Пересечение сферы плоскостью общего положения |
1. Произведем замену плоскостей проекций таким образом, чтобы плоскость α стала проецирующей, т.е. переведем плоскость общего положения в частное. h – горизонталь, f - фронталь, чтобы перевести плоскость α в положение проецирующей плоскости необходимо выбрать новую плоскость проекций, либо перпендикулярно горизонтальной проекции горизонтали h 1, либо перпендикулярно фронтальной проекции фронталь – f 2 (рис.8.20).
2. Дальнейшее решение аналогично предыдущей задаче.
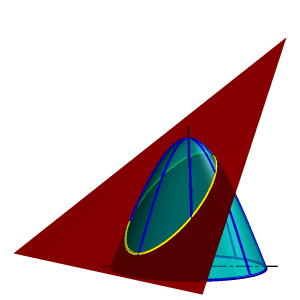
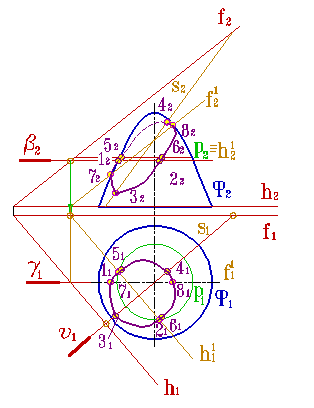
Рассмотрим еще один способ решения позиционной задачи по определению линии, пересечения поверхности вращения и плоскости общего положения, заданной двумя пересекающимися прямыми α (h∩f) (рис.8.21).
| 
| |
| а) модель | б) эпюр | |
| Рисунок 8.21. Пересечение параболоида вращения плоскостью общего положения |
Сечение поверхности Ф плоскостью α (h∩f) и проекции этого сечения на плоскость, перпендикулярную оси i, являются кривыми, имеющими ось симметрии. Для доказательства этого утверждения проведем вспомогательную плоскость β, перпендикулярную оси i. Вспомогательная плоскость пересечет заданную поверхность по параллели p, фронтальная проекция которой p 2, совпадает со следом плоскости β 2, а горизонтальная проекция p 1 - является окружностью. Линией пересечения вспомогательной плоскости с заданной плоскостью α (h∩f) является горизонталь h 1.
Параллель p и горизонталь h 1, находясь в одной плоскости β, пересекаются в точках 1 и 2, которые принадлежат искомой линии. Полученные точки симметричны друг другу относительно плоскости σ, перпендикулярной хорде 1-2 и проходящей через ее середину. Заметим, что плоскость σ, являясь множеством точек, равноудаленных от концов хорды 1 - 2, пройдет через ось i поверхности вращения, все точки которой также равноудалены от точек 1 и 2.
Очевидно, что для любой другой пары точек, расположенных на концах хорд других окружностей (но параллельных хорде 1-2), плоскость σ будет также являться плоскостью симметрии. Следовательно, кривая сечения поверхности вращения плоскостью α представляет собой кривую симметричную, осью симметрии которой служит линия пересечения плоскостей α и σ – прямая, пересекающая поверхность в точках 3 и 4 (линия наибольшего ската плоскости α проходящая через ось поверхности вращения).
Таким образом, используя вспомогательные горизонтальные секущие плоскости можно получить необходимое множество точек для построения линии пересечения плоскости α и поверхности Ф, которой является эллипс. Поэтому для более точного построения необходимо учитывать точки, определяющие положение осей эллипса (3, 4, 5 и 6)
Однако, если не учитывать характерные точки, определяющие границу зоны видимости линии пересечения и высшую и низшую точки этой линии, построение будет неточным.
Точки, определяющие зону видимости- 7 и 8, расположены на главном меридиане поверхности. Для построения их, через главный меридиан проведем вспомогательную секущую плоскость γ, параллельную фронтальной плоскости проекций. Плоскость γ пересекает плоскость α по фронтали f 1, которая, в свою очередь, находясь в одной плоскости с главным меридианом, пересекается с ним в искомых точках 7 и 8.
Высшая и низшая точки сечения - 3 и 4 находятся на линии наибольшего ската плоскости α, проходящей через ось поверхности Ф т.е. на прямой s. Эту прямую и меридиан поверхности, плоскость которого совпадает с прямой s, повернем вокруг оси i до положения s 1, когда прямая s и плоскость меридиана окажутся параллельными П 2. Отметим при этом, что точка К пересечения прямой s и осью i остается неподвижной, а вращаемый меридиан в итоге совместится с главным меридианом- очерком фронтальной проекции поверхности вращения. Отметим точки пересечения фронтальной проекции главного меридиана и повернутой прямой. Возвращая обратным поворотом прямую s с найденными точками в исходное положение, находим положение точек 3 и 4.
Соединив, полученные точки кривой с учетом видимости получим линию пересечения плоскости α с поверхностью Ф.
| Конические сечения. |
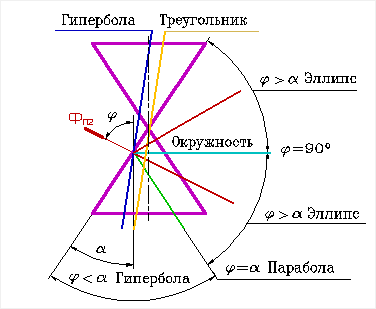Рисунок 8.22. Конические сечения
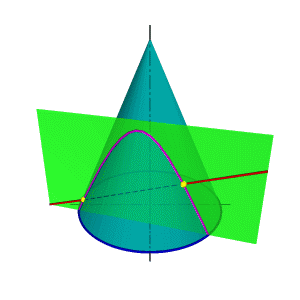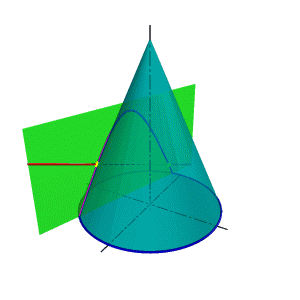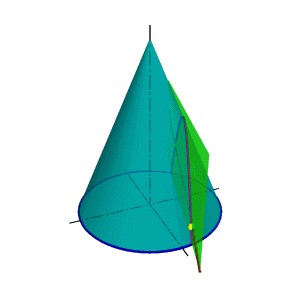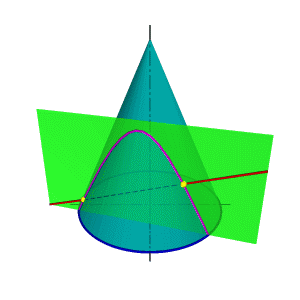
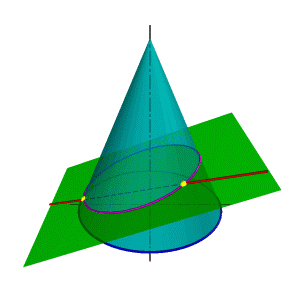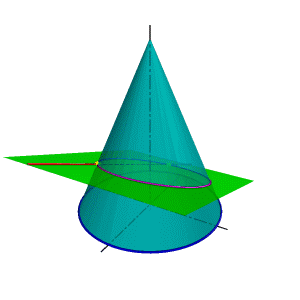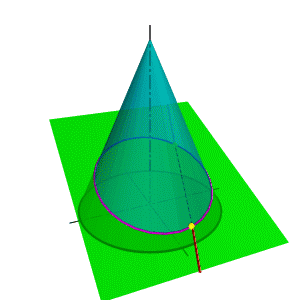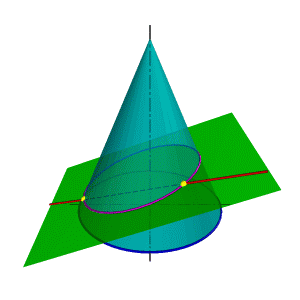
| В зависимости от положения секущей плоскости линиями сечения конической поверхности могут быть (рис.8.22): эллипс, парабола, гипербола, а в частных случаях: окружность, прямая, две пересекающиеся прямые и точка. Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ > α, то линией сечения является эллипс (рис.8.23) В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса. В частном случае (φ= 900) такая плоскость пересекает поверхность конуса по окружности (рис.8.24); и сечение вырождается в точку, если плоскость проходит через вершину конуса. Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ = α, то линией пересечения является парабола (рис.8.25). В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в прямую. |
| 
|
| Рисунок 8.23. Эллипс | Рисунок 8.24. Окружность |
| 
|
| Рисунок 8.25. Парабола | Рисунок 8.26. Гипербола |
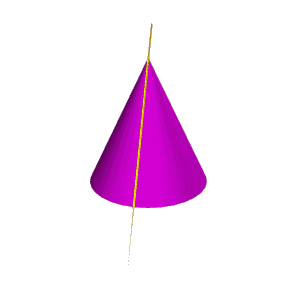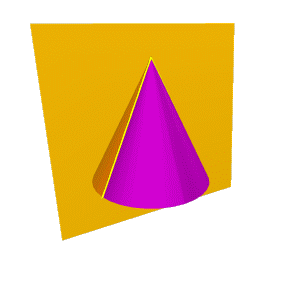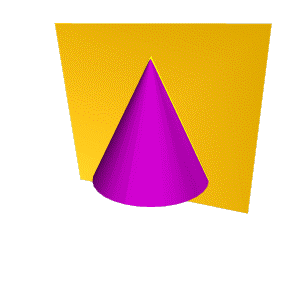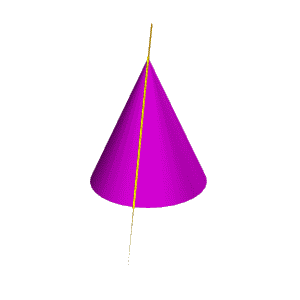
| Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), т.е. φ < α, то линией сечения является гипербола (рис.8.26). В случае прохождения плоскости через вершину конической поверхности фигурой сечения могут быть сами образующие, т.е. гипербола вырождается в две пересекающие прямые (рис.8.27). |
| Рисунок 8.27. Пересекающиеся прямые |
Лекция №8 часть 3
Метод вспомогательных секущих плоскостей. Метод вспомогательных секущих сфер.
Частные случаи пересечения поверхностей второго порядка.
| Пересечение линии с поверхностью |
| В общем случае для графического определения точек пересечения линии с поверхностью (рис.8.28) необходимо выполнить ряд геометрических построений, описываемых следующим алгоритмом: 1. Заключаем линию l в некоторую вспомогательную поверхность Δ; 1. Строим линию m пересечения данной поверхности Ф и вспомогательной поверхности Δ; 2. Определяем искомую точку К пересечения линии l и m (точка может быть не единственная). В качестве вспомогательной поверхности целесообразно использовать проецирующую цилиндрическую поверхность, направляющей которой должна служить заданная линия, а –прямолинейными образующими – проецирующие прямые. Пример: Определить точки пересечения прямой линии с поверхностью конуса вращения и определить видимость прямой по отношению к конусу. Если в качестве вспомогательной секущей плоскости можно выбрать горизонтально проецирующую или фронтально проецирующую плоскости, то в сечении получатся соответственно гипербола (рис.8.29а) или эллипс (рис.8.29б). Построение кривых линий значительно усложняет задачу. | |
| Рисунок 8.28. Пересечение линии с поверхностью | ||
| 
|
| а) горизонтально проецирующая плоскость | б) фронтально проецирующая плоскость |
| Рисунок 8.29 Пересечение прямой линии с конусом (вспомогательная секущая плоскость- проецирующая плоскость) |
| 
| ||||
| а) модель | б) эпюр | ||||
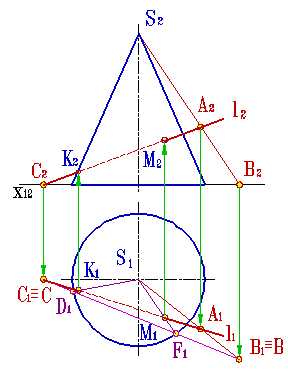
| Рисунок 8.30. Пересечение прямой линии с конусом (вспомогательная секущая плоскость-плоскость общего положения) | |||||
Поэтому в качестве вспомогательной секущей плоскости целесообразно выбрать такую плоскость, которая бы включала прямую l и пересекала конус по образующим (рис.8.30). Очевидно, что такая плоскость определяется прямой l и точкой S - вершиной конуса. Пусть основание конуса лежит в горизонтальной плоскости проекций, тогда линия пересечения вспомогательной секущей плоскости и горизонтальной плоскости проекций ВС пересекает основание конуса в точках D и F. Таким образом в сечении конуса вспомогательной секущей плоскостью получится треугольник DFS. Так как полученный треугольник и прямая l лежат в одной плоскости, точки их пересечения К и М и есть точки пересечения прямой с конусом.
| Взаимное пересечение поверхностей |
Линией пересечения двух поверхностей является множество точек, общих для данных поверхностей. Из этого множества выделяют характерные (опорные, или главные) точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно изменять положение вспомогательных секущих поверхностей для определения остальных точек.
К таким точкам относятся: экстремальные точки- верхняя и нижняя точки относительно той или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей точки границы зоны видимости и т.д.
Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей.
Иногда целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности (или одну из них) в частном положении.
Для определения этих точек часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.
Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.
Из общей схемы построения линии пересечения поверхностей выделяют два основных метода - метод секущих плоскостей и метод секущих сфер.
В общем случае решение задачи по построении линии пересечения двух поверхностей может быть сведено к рассмотренным ранее задачам по определению:
1. Точек пересечения линии с поверхностью;
2. Линии пересечения плоскости и поверхности;
3. Комбинации первой и второй задачи.
| Метод вспомогательных секущих плоскостей. |
Вспомогательные секущие плоскости чаще всего выбирают проецирующими и параллельными одной из плоскостей проекций - плоскостями уровня.
Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:
1. Если образующие (окружности) расположены в общих плоскостях уровня;
2. Если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;
3. Линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.
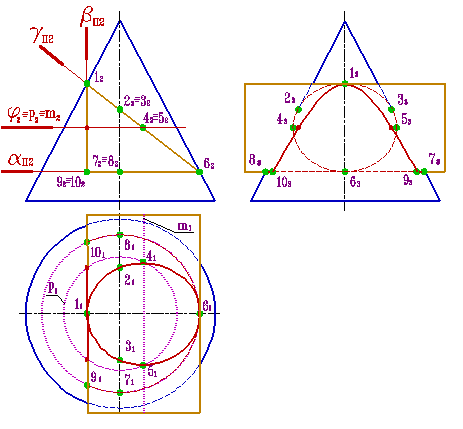
| Пример 1:Рассмотрим построение линии пересечения треугольной призмы с конусом (рис.8.31). Пусть ось вращения конуса перпендикулярна плоскости П 1, а грани призмы перпендикулярны плоскости П 2. В этом случае призму можно рассматривать, как три плоскости α, β, γ, проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом. При этом в соответствии с характерными сечениями конуса известно, что плоскость α пересекает конус по окружности параллельной П 1, β- по гиперболе параллельной П 3, а γ - по эллипсу. На плоскость П 2 линии пересечения от всех плоскостей проецируются в прямые, совпадающие со следами плоскостей α, β, и γ. Для построения проекций этих линий на плоскости П 1 и П 3 отметим характерные точки на уже имеющейся фронтальной проекции линий пересечения: |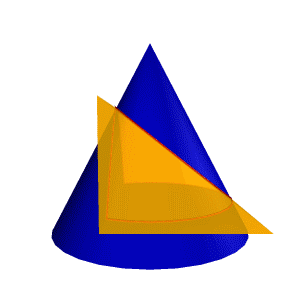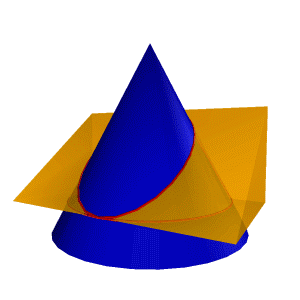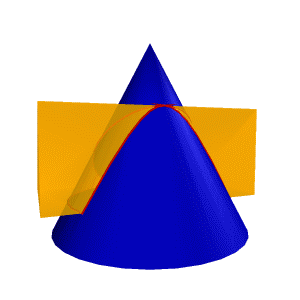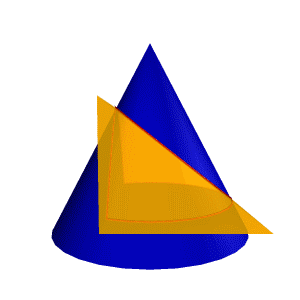 
| |
| а) модель | ||
| ||
| б) эпюр | ||
| Рисунок 8.31. Пересечение конуса и призмы | ||
Точки 12 и 62 – пересечения плоскости γ с очерком проекции конуса на плоскость П 2 (главным меридианом), эти точки определяют положение большой оси эллипса, кроме того точка 12 –проекция точки вершины гиперболы и одновременно принадлежит конусу (лежит на очерке фронтальной проекции конуса) и ребру призмы (линии пересечения плоскостей α и β), а точка 62 - проекция точки, одновременно принадлежащей конусу и ребру призмы (линии пересечения плоскостей α и γ); точки 2, 3, 7 и 8 – характерны тем, что их профильные проекции лежат на очерке проекции конуса; 42, 52 - точки, лежащие на середине отрезка 1262 (большой оси эллипса) и определяют положение малой оси эллипса; 9,10 – точки одновременно принадлежащие конусу и ребру призмы (образованному пересечением плоскостей α и β).
Рассмотрим последовательность нахождения проекций точек 4 и 5. Через фронтальные проекции этих точек проведем вспомогательную секущую плоскость φ. Эта плоскость пересекает конус по параллели p, а грань призмы по прямой линии m, параллельной ребру. На горизонтальной плоскости проекций пересечение p 1 и m 1 определяют положение точек 41 и 51. Для точного построения кривых линий пересечения поверхностей обозначенных точек не достаточно. После нахождения проекций всех точек их необходимо соединить с учетом видимости.
| Пример 2: Пересечение сферы и цилиндра (рис.8.32).В данном примере вспомогательные плоскости уровня могут быть параллельными плоскостям П 2 и П 1. В первом случае фронтальные плоскости пересекают сферу по окружности, а цилиндр по прямолинейным образующим. Одна из таких плоскостей α пересекается с поверхностями по дуге окружности a и прямой линии b. Точка 1 пересечения дуги окружности а и прямой b принадлежат искомой кривой. |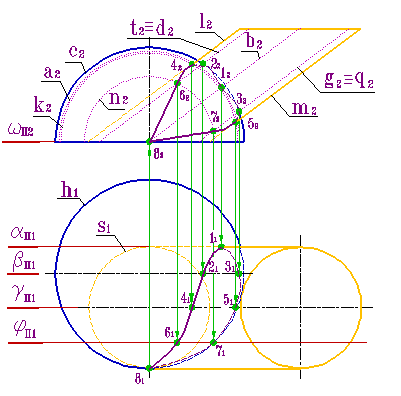 
| |
| ||
| а) модель | б) эпюр | |
| Рисунок 8.32. Пересечение полусферы и эллиптического цилиндра |
С помощью вспомогательной секущей плоскости b (плоскости главного фронтального меридиана полусферы) найдены точки 2 и 3, как точки пересечения главного фронтального меридиана полусферы - дуги окружности с с линиями d и g. Плоскость g - плоскость главного фронтального меридиана цилиндра, пересекает полусферу по дуге окружности - k которая в свою очередь пересекаясь с фронтальным меридианом цилиндра l и m определяет положение точек 4 и 5. Аналогично, с помощью плоскости j найдены точки 6 и 7.
Точка 8 найдена с помощью фронтально проецирующей плоскости w, параллельной горизонтальной плоскости проекций, которая пересекает полусферу по окружности - экватору h, а цилиндр по окружности основания s.
Характерными точками, в данном случае, являются точки 1- 5 и 8, лежащие на очерках проекций поверхностей. Кроме того, точки 1 и 8 определяют границу зоны видимости кривой на плоскость П 1, а точки 4 и 5 – границу зоны видимости на плоскость П 2.
| Метод вспомогательных секущих сфер. |
При определении линии пересечения двух поверхностей вращения, при их особом взаимном расположении, не всегда рационально применять вспомогательные секущие плоскости. В некоторых случаях применяют метод вспомогательных секущих сфер – концентрических или эксцентрических.
| Концентрические сферические посредники применяются при определении линии пересечения двух поверхностей вращения с пересекающимися осями. Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических сфер должно предшествовать такое преобразование чертежа в результате которого оси обеих поверхностей должны быть расположены параллельно одной и той же плоскости проекций (рис.8.33) или одна из осей становиться проецирующей прямой, а вторая - линией уровня (рис.34). |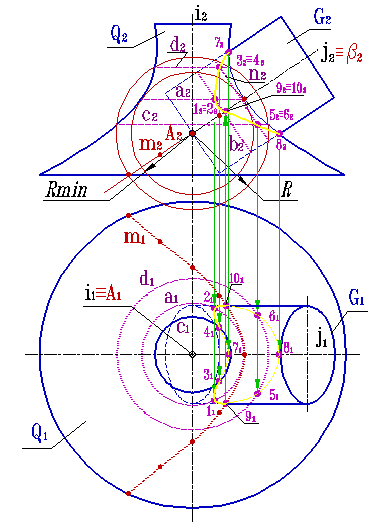 
| ||||
| |||||
| а) модель | б) эпюр | ||||
| Рисунок 8.33. Пересечение поверхностей вращения, оси которых параллельны фронтальной плоскости проекций. | |||||
Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А (рис.8.33). Эта точка принимается за центр всех вспомогательных концентрических сфер. Каждая из концентрических сфер пересекает поверхности по окружностям - параллелям (а, b, c, d, n), фронтальные проекции которых являются прямыми линиями (а 2, b 2, c 2, d 2, n 2). Проекции точек 1 2, 2 2, 3 2, 4 2, 5 2 и 6 2 пересечения проекций параллелей принадлежат проекции искомой линии пересечения поверхностей. Пересечение главных меридианов определяет крайние точки 7 и 8.
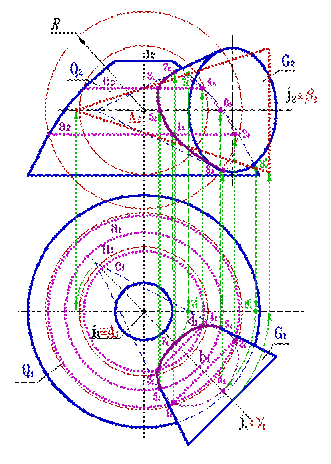
| Для точного построения линии пересечения поверхностей необходимо найти точки 9 и 10, которые определяют границу зоны видимости линии пересечения поверхностей на горизонтальной проекции. Для этой цели использовалась вспомогательная секущая плоскость b, которая пересекает поверхность Q по линии m, а поверхность G по образующим, горизонтальные проекции которых пересекаясь определяют положение искомых точек. Соединив найденные точки 1... 10 с учетом видимости получим линию пересечения поверхностей. Вторым примером использования в качестве вспомогательных поверхностей посредников концентрических сфер рассмотрим при определении линии пересечения поверхностей предложенных на рисунке 8.34. Оси поверхностей вращения G и Q пересекаются в точки А, при этом ось поверхности Q - фронтально проецирующая прямая, а ось поверхности G - горизонталь. Точка А принимается за центр всех вспомогательных концентрических сфер. Точки 1 и 2 линии пересечения построены с помощью сферы радиуса R. Эта сфера пересекает поверхность Q по окружности а, а поверхность G по окружности в, которая показана только на горизонтальной проекции. Пересечение горизонтальных проекций окружностей а 1 и в 1 определяют проекции 1 1 и 2 1 точек линии пересечения. Их фронтальные проекции 1 2 и 2 2 построены на а 2 пересечении с линиями связи. Аналогично найдены точки 3 и 4. Для нахождения точек 5 и 6 определяющих границу зоны видимости на горизонтальной проекции использовалась вспомогательная секущая плоскость b, которая пересекает поверхность Q по окружность n, а коническую поверхность G по треугольнику определяющему ее очерк на горизонтальной проекции. Точки 7 и 8 находятся на границе зоны видимости фронтальной проекции, для их нахождения используется вспомогательная секущая плоскость g. Соединив найденные точки 1... 8 с учетом видимости получим линию пересечения поверхностей G и Q. |
| Рисунок 8.34. Пересечение поверхностей вращения, ось одной - горизонтально проецирующая прямая, а второй - горизонталь |
| Эксцентрические сферические посредники применяются при определении точек линии пересечения поверхностей вращения с поверхностью несущей на себе непрерывное множество окружностей. Обе поверхности должны иметь общую плоскость симметрии. Вспомогательные эксцентрические сферы пересекаются с данными поверхностями по окружностям. |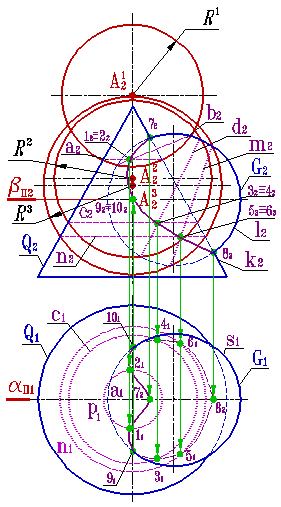 
| ||||
| |||||
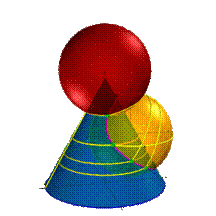
| а) модель | б) эпюр | ||||
| Рисунок 8.35. Пересечение конуса и сферы | |||||
Определения линии пересечения конуса и сферы применение эксцентричных сфер, как поверхностей - посредников. Центры сфер - точки расположены на оси конуса. Сфера пересекает конус и сферу по окружностям, которые пересекаются в двух точках, принадлежащих искомой линии пересечения (рис.8.35а).
Верхняя и нижняя точки линии пересечения найдены с помощью вспомогательной секущей плоскости - плоскости главного фронтального меридиана, пересекающая конус и сферу по треугольнику и окружности, являющимися очерками поверхностей на фронтальной плоскости проекций.
Точки определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости - горизонтальной плоскости уровня, пересекающей сферу по экватору - окружности являющейся очерком шара на горизонтальной проекции, а конус по окружности - параллели.
Найденные с помощью вспомогательных поверхностей посредников точки определяют линию пересечения конуса и шара.
Рассмотрим на примере определения линии пересечения конуса Q и сферы G (рис.8.35б) применение эксцентричных сфер, как поверхностей - посредников. Центры сфер - точки А 1, А 2 и А 3 расположены на оси конуса. Сфера радиуса R 1 с центром в точке А 1 пересекает конус и сферу по окружностям а и в, которые пересекаются в точках 1 и 2, принадлежащих искомой линии пересечения. С помощью сферы R 2 с центром А 2 исферы R 3 с центром А 3 определено положение точек 3, 4 и 5, 6 соответственно. Точки 7 и 8 найдены с помощью вспомогательной секущей плоскости a (плоскости фронтального меридиана), пересекающая конус и сферу по главном фронтальном меридианам k и l. Точки 9 и 10, определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости b (горизонтальной плоскости уровня), пересекающей сферу G по экватору s, а конус Q по окружности p. Найденные с помощью вспомогательных поверхностей посредников точки 1...10 определяют линию пересечения конуса и шара.
| Частные случаи пересечения поверхностей второго порядка |
Поверхностью второго порядка называется множество точек пространства, декартовы координаты, которых удовлетворяют алгебраическому уравнению второй степени.
Две поверхности второго порядка в общем случае пересекаются по пространственной линии четвертого порядка, которую называют биквадратной кривой.
В некоторых случаях биквадратная кривая распадается на две плоские кривые второго порядка, причем одна из них может быть мнимой.
Опуская доказательства, приведем некоторые теоремы и примеры, иллюстрирующие их применение.
