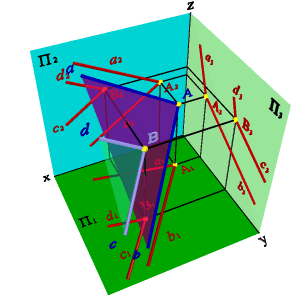
Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d.
Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой.
Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой
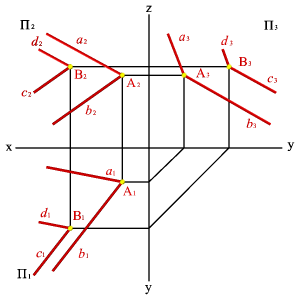
d // a, с // b Þ d 1 a 1, с 1// b 1; d 2 a 2, с 2// b 2; d 3 a 3, с 3// b 3.
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 5.24. Параллельные плоскости | |||
2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.
Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.5.25).
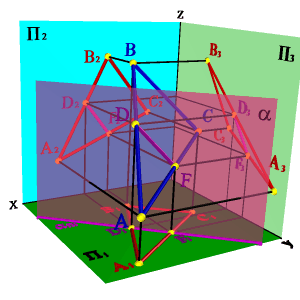
Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость - горизонтально проецирующая a.
Требуется построить линию пересечения плоскостей.
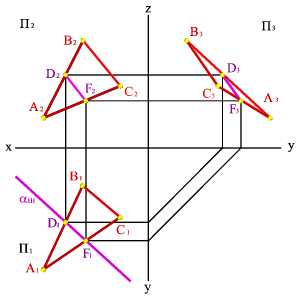
Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью a - точка D, прямой (AС) - F. Отрезок [ DF ] определяет линию пересечения плоскостей. Так как a - горизонтально проецирующая плоскость, то проекция D 1 F 1 совпадает со следом плоскости a П1, таким образом остается только построить недостающие проекции [ DF ] на П2 и П3.
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 6.25. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью | |||
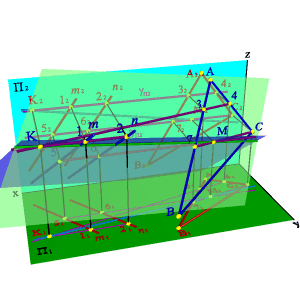
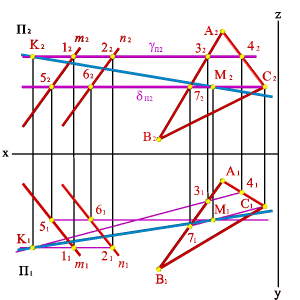
Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a (n,m) и b (ABC) (рис.5.26).
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 5.26. Пересечение плоскостей общего положения | |||
Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точка К - точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b - прямая (КМ).
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.
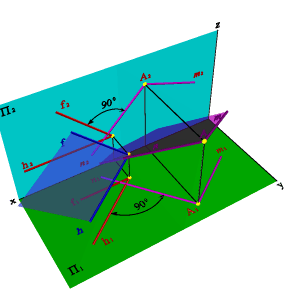
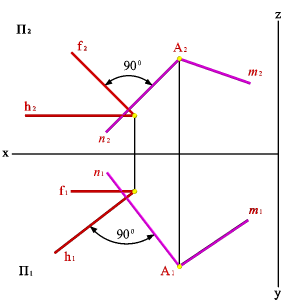
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a. Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.5.27).
| 
| |
| а) модель | б) эпюр | |
| Рисунок 5.27. Взаимно перпендикулярные плоскости |
Лекция №6-1
Многогранники
Многогранником называется совокупность таких плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого (но только одного).
| Виды многогранников |
Кратко охарактеризуем геометрические свойства некоторых многогранников:
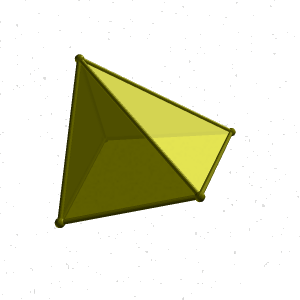
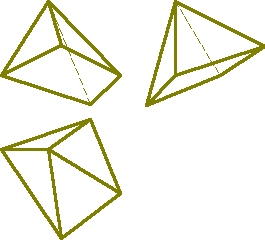
1. Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.6.1.).
| 
|
| а) модель | б) эпюр |
| Рисунок 6.1. Пирамида |
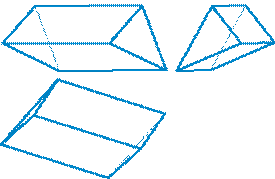
2. Призма - многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис 6.2.).
| 
|
| а) модель | б) эпюр |
| Рисунок 6.2. Призма |
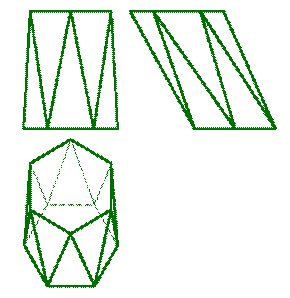
3. Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники и трапеции, вершины которых являются и вершинами многоугольников оснований (рис.6.3.).
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 6.3. Призматоид | |||
4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными Углы при вершинах такого многогранника равны между собой.
Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.
Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
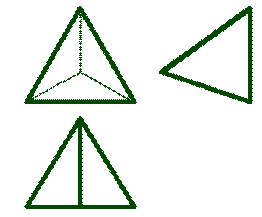
Тетраэдр - правильный четырехгранник (рис 6.4.). Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).
| 
|
| а) модель | б) эпюр |
| Рисунок 6.4. Тетраэдр |
Гексаэдр - правильный шестигранник (рис. 6.5.). Это куб состоящий из шести равных квадратов.
| 
|
| а) модель | б) эпюр |
| Рисунок 6.5. Гексаэдр |
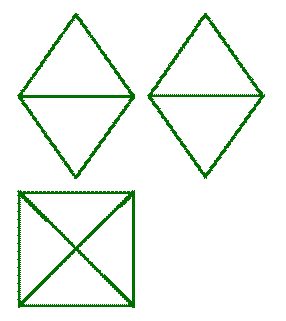
Октаэдр - правильный восьмигранник (рис.6.6.). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.
| 
|
| а) модель | б) эпюр |
| Рисунок 6.6. Октаэдр |
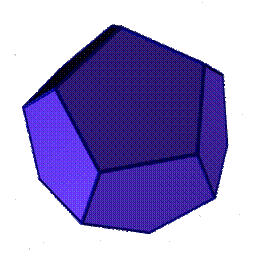
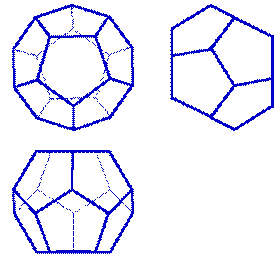
Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 6.7.).
| 
|
| а) модель | б) эпюр |
| Рисунок 6.7. Додекаэдр |
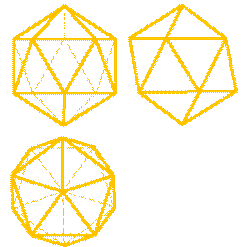
Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.6.8.).
| 
|
| а) модель | б) эпюр |
| Рисунок 6.8. Икосаэдр |
5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.
Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру (рис. 6.9.). Это малые тетраэдры основания которые совпадают с гранями октаэдра. его можно рассматривать как соединение двух пересекающихся тетраэдров центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.
| 
|
| Рисунок 6.9. Звездчатый октаэдр | Рисунок 6.10. Малый звездчатый додекаэдр |
Малый звездчатый додекаэдр - (рис.6.10) звездчатый додекаэдр первого продолжения. Он образован продолжением граней выпуклого додекаэдра до их первого пересечения. Каждая грань выпуклого додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые "куски", внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра. При дальнейшем продолжении граней до нового пересечения образуется средний звездчатый додекаэдр - звездчатый додекаэдр второго продолжения. Последней же звездчатой формой правильного додекаэдра является звездчатый додекаэдр третьего продолжения - большой звездчатый додекаэдр. Он образован продолжением граней звездчатого додекаэдра второго продолжения до их нового пересечения.
Лекция №6-2
| Пересечение плоскости с многогранником |
Построение сечения многогранника требует многократного решения задачи о нахождении точки пересечении прямой с плоскостью. Точки, в которых ребра многогранника пересекаются с заданной плоскостью, будут вершинами искомого сечения.
Тот же результат можно получить, сведя задачу к построению прямых пересечения плоскости с гранями тела.
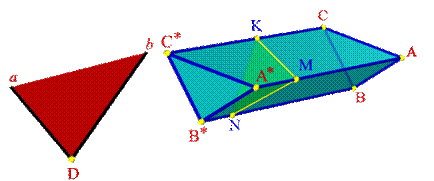
Дана призма и плоскость общего положения заданная двумя пересекающимися прямыми а и в (рис.6.11). Необходимо найти сечение призмы данной плоскостью.
| |||
| а) модель | |||
| |||
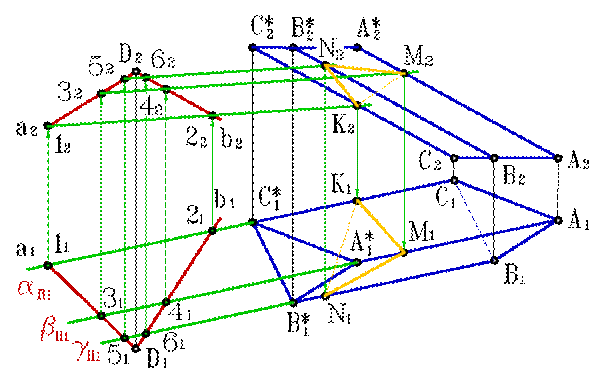
| б) эпюр | |||
| Рисунок 6.11. Пересечение плоскости общего положения с призмой | |||
Решим поставленную задачу нахождением точек пересечения ребер призмы с плоскостью. Для чего, через горизонтальные проекции ребер проведем вспомогательные секущие плоскости α, β и γ. Построив линии пересечения вспомогательных плоскостей с заданной, находим на фронтальной проекции точки пересечения их с соответствующими ребрами призмы К 2, М 2 и N 2 – вершины фронтальной проекции сечения призмы. По линиям связи находим горизонтальные проекции этих точек. Полученные точки соединяем прямыми линиями, с учетом видимости. При решении вопроса о видимости сторон построенного сечения следует иметь в виду достаточно очевидное правило: точка и линия, лежащие на поверхности многогранника, видимы только в том случае, если они расположены на видимой грани.
| Пересечение прямой линии с многогранником |
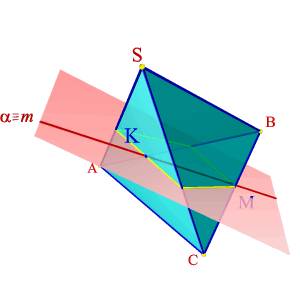
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с плоскостями граней (рис.6.12).
| Алгоритм решения задачи: 1. Провести плоскость a: mÎa. 2. Построить сечение многогранника плоскостью a. Определить искомые точки К,М - пересечения полученного сечения с прямой m. |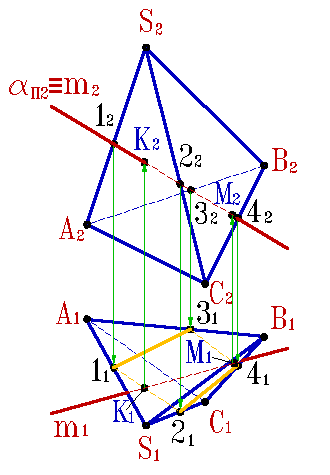 
| ||
| |||
| а) модель | б) эпюр | ||
| Рисунок 6.12. Пересечение прямой линии с пирамидой | |||
| Взаимное пересечение многогранников |
Построение линии взаимного пересечения многогранных поверхностей можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:
1. Определяют точки, в которых ребра одной из многогранных поверхностей пересекают грани другой и ребра второй пересекают грани первой (задача на пересечение прямой с плоскостью). Через найденные точки в определенной последовательности проводят ломаную линию, представляющую собой линию пересечения данных многогранников. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.
2. Определяют отрезки прямых, по которым грани одной поверхности пересекают грани другой (задача на пересечение двух плоскостей между собой); эти отрезки являются звеньями ломаной линии, получаемой при пересечении многогранных поверхностей.
| Если проекция ребра одной из поверхностей не пересекает проекции грани другой хотя бы на одной из проекций, то данное ребро не пересекает этой грани. Однако пересечение проекций ребра и грани еще не означает, что ребро и грань пересекаются в пространстве. |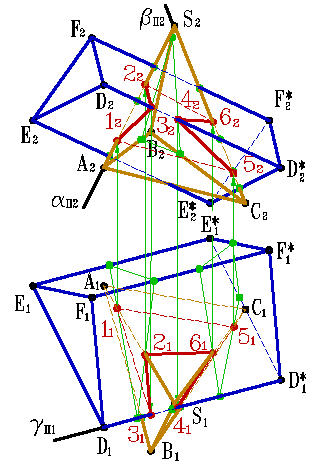 
| |
| ||
| а) модель | б) эпюр | |
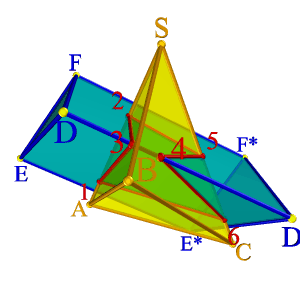
| Рисунок 6.13. Пересечение пирамиды с призмой |
На примере (рис.6.13) показано пересечение поверхности треугольной призмы с треугольной пирамидой. Построение основано на нахождении точек пересечения ребер одного многогранника с гранями другого. На рисунке 6.13 б показано построение линии пересечения пирамиды АВСS и треугольной призмы DEFD*E*F*.
Для нахождения точек 1 и 2 в которых ребро пирамиды AS пересекает грани DD*EE* и EE*FF* призмы, через проекцию ребра A 2 S 2 проведена фронтально проецирующая плоскость α П2, которая пересекает ребра призмы в трех точках, горизонтальные проекции этих точек пересечения плоскости α с ребрами призмы, образуют треугольник. Проекция ребра пирамиды A 1 S 1 пересекаетполученный треугольник в точках 1 1 и 2 1.
С помощью фронтально - проецирующей плоскости β, находим точки 5 и 6 пересечения ребра пирамиды SC с гранями призмы EE*FF* и EE*DD*, а при помощи горизонтально проецирующей плоскости γ находим точки 3 и 4 пересечения ребра призмы с гранями пирамиды. Соединив полученные точки, с учетом видимости, получим пространственную ломаную линию – линию пересечения данных многогранников.
Лекция №7-1
| Кривые линии |
Кривая линия - это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному. В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством и т.д.
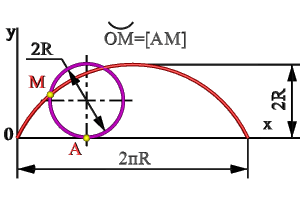Рисунок 7.1 Циклоида
| Например, (рис.7.1) циклоида – траектория движения точки окружности, катящейся без скольжения по прямой линии. Эта кривая состоит их ряда «арок», каждая из которых соответствует полному обороту окружности. Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные пространственными. Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую. |
Различны и способы задания кривых:
· Аналитический – кривая задана математическим уравнением;
· Графический – кривая задана визуально на носителе графической информации;
· Табличный – кривая задана координатами последовательного ряда точек.
Уравнением кривой линии называется такое соотношение между переменными, которому удовлетворяют координаты точки, принадлежащей кривой.
