5.1Построение модели произвести на примере уровня производительности труда рабочих промышленного предприятия (таблица 5.1).
Таблица 5.1 - Исходные данные
Таблица 5.1 - Исходные данные
| № предприятия | У 1 | У 2 | У 3 | Х 4 | Х 5 | Х 6 | Х 7 | Х 8 | Х 9 | Х 10 | Х 11 | Х 12 | Х 13 | Х 14 | Х 15 | Х 16 | Х 17 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9,26 | 204,20 | 13,26 | 0,23 | 0,78 | 0,40 | 1,37 | 1,23 | 0,23 | 1,45 | 167,69 | 6,40 | 166,32 | 10,08 | 17,72 | |||
| 9,38 | 209,60 | 10,16 | 0,24 | 0,75 | 0,26 | 1,49 | 1,04 | 0,39 | 1,30 | 186,10 | 7,80 | 92,88 | 14,76 | 18,39 | |||
| 12,11 | 222,60 | 13,72 | 0,19 | 0,68 | 0,40 | 1,44 | 1,80 | 0,43 | 1,37 | 220,45 | 9,76 | 158,04 | 6,48 | 26,46 | |||
| 10,81 | 236,70 | 12,85 | 0,17 | 0,70 | 0,50 | 1,42 | 0,43 | 0,18 | 1,65 | 169,30 | 7,90 | 93,96 | 21,96 | 22,37 | |||
| 9,35 | 62,00 | 10,63 | 0,23 | 0,62 | 0,40 | 1,35 | 0,88 | 0,15 | 1,91 | 39,53 | 5,35 | 173,88 | 11,88 | 28,13 | |||
| 9,87 | 53,10 | 9,12 | 0,43 | 0,76 | 0,19 | 1,39 | 0,57 | 0,34 | 1,68 | 40,41 | 9,90 | 162,30 | 12,60 | 17,55 | |||
| 8,17 | 172,10 | 25,83 | 0,31 | 0,73 | 0,25 | 1,16 | 1,72 | 0,38 | 1,94 | 102,96 | 4,50 | 88,56 | 11,52 | 21,92 | |||
| 9,12 | 56,50 | 23,39 | 0,26 | 0,71 | 0,44 | 1,27 | 1,70 | 0,09 | 1,89 | 37,02 | 4,88 | 101,16 | 8,28 | 19,52 | |||
| 5,88 | 52,60 | 14,68 | 0,49 | 0,69 | 0,17 | 1,16 | 0,84 | 0,14 | 1,94 | 45,74 | 3,46 | 166,32 | 11,52 | 23,99 | |||
| 6,30 | 46,60 | 10,05 | 0,36 | 0,73 | 0,39 | 1,25 | 0,60 | 0,21 | 2,06 | 40,07 | 3,60 | 140,76 | 32,40 | 21,76 | |||
| 6,22 | 53,20 | 13,99 | 0,37 | 0,68 | 0,33 | 1,13 | 0,82 | 0,42 | 1,96 | 45,44 | 3,56 | 128,52 | 11,52 | 25,68 | |||
| 5,49 | 30,10 | 9,68 | 0,43 | 0,74 | 0,25 | 1,10 | 0,84 | 0,05 | 1,02 | 41,08 | 5,65 | 177,84 | 17,28 | 18,13 | |||
| 6,50 | 146,40 | 10,03 | 0,35 | 0,66 | 0,32 | 1,15 | 0,67 | 0,29 | 1,85 | 136,14 | 4,28 | 114,48 | 16,20 | 25,74 | |||
| 6,61 | 18,10 | 9,13 | 0,38 | 0,72 | 0,02 | 1,23 | 1,04 | 0,48 | 0,88 | 42,39 | 8,85 | 93,24 | 13,32 | 21,21 | |||
| 4,32 | 13,60 | 5,37 | 0,42 | 0,68 | 0,06 | 1,39 | 0,66 | 0,41 | 0,62 | 37,39 | 8,52 | 126,72 | 17,28 | 22,97 | |||
| 7,37 | 89,80 | 9,86 | 0,30 | 0,77 | 0,15 | 1,38 | 0,86 | 0,62 | 1,09 | 101,78 | 7,19 | 91,80 | 9,72 | 16,38 | |||
| 7,02 | 62,50 | 12,62 | 0,32 | 0,78 | 0,08 | 1,35 | 0,79 | 0,56 | 1,60 | 47,55 | 4,82 | 69,12 | 16,20 | 13,21 | |||
| 8,25 | 46,30 | 5,02 | 0,25 | 0,78 | 0,20 | 1,42 | 0,34 | 1,76 | 1,53 | 59,75 | 32,61 | 5,46 | 66,24 | 24,84 | 14,48 | ||
| 8,15 | 103,50 | 21,18 | 0,31 | 0,81 | 0,20 | 1,37 | 1,60 | 1,31 | 1,40 | 103,25 | 6,20 | 67,68 | 14,76 | 13,38 | |||
| 8,72 | 73,30 | 25,17 | 0,26 | 0,79 | 0,30 | 1,41 | 1,46 | 0,45 | 2,22 | 38,95 | 4,25 | 50,40 | 7,56 | 13,69 | |||
| 6,64 | 76,60 | 19,40 | 0,37 | 0,77 | 0,24 | 1,35 | 1,27 | 0,50 | 1,32 | 81,32 | 5,38 | 70,56 | 8,64 | 16,66 | |||
| 8,10 | 73,10 | 21,01 | 0,29 | 0,78 | 0,10 | 1,48 | 1,58 | 0,77 | 1,48 | 67,26 | 5,88 | 72,00 | 8,64 | 15,06 | |||
| 5,52 | 32,30 | 6,57 | 0,34 | 0,72 | 0,11 | 1,24 | 0,68 | 1,20 | 0,68 | 59,92 | 9,27 | 97,20 | 9,00 | 20,09 | |||
| 9,37 | 199,60 | 14,19 | 0,23 | 0,79 | 0,47 | 1,40 | 0,86 | 0,21 | 2,30 | 107,34 | 4,36 | 80,28 | 14,76 | 15,98 | |||
| 13,17 | 598,10 | 15,81 | 0,17 | 0,77 | 0,53 | 1,45 | 1,98 | 0,25 | 1,37 | 512,60 | 10,31 | 51,48 | 10,08 | 18,27 | |||
| 6,67 | 71,20 | 5,23 | 0,29 | 0,80 | 0,34 | 1,40 | 0,33 | 0,15 | 1,51 | 53,81 | 4,69 | 105,12 | 14,76 | 14,42 | |||
| 5,68 | 90,80 | 7,99 | 0,41 | 0,71 | 0,20 | 1,28 | 0,45 | 0,66 | 1,43 | 80,83 | 4,16 | 128,52 | 10,44 | 22,76 | |||
| 5,22 | 82,10 | 17,50 | 0,41 | 0,79 | 0,24 | 1,33 | 0,74 | 0,74 | 1,82 | 59,42 | 3,13 | 94,68 | 14,76 | 15,41 | |||
| 10,02 | 76,20 | 17,16 | 0,22 | 0,76 | 0,54 | 1,22 | 0,03 | 0,32 | 2,62 | 36,96 | 4,02 | 85,32 | 20,52 | 19,35 | |||
| 8,16 | 119,50 | 14,54 | 0,29 | 0,78 | 0,40 | 1,28 | 0,99 | 0,89 | 1,75 | 91,43 | 5,23 | 76,32 | 14,40 | 16,83 | |||
| 3,78 | 21,90 | 6,24 | 0,51 | 0,62 | 0,20 | 1,47 | 0,24 | 0,23 | 1,54 | 17,16 | 2,74 | 153,00 | 24,84 | 30,53 | |||
| 6,48 | 48,40 | 12,08 | 0,36 | 0,75 | 0,64 | 1,27 | 0,57 | 0,32 | 2,25 | 27,29 | 3,10 | 107,64 | 11,16 | 17,98 | |||
| 10,44 | 173,50 | 9,49 | 0,23 | 0,71 | 0,42 | 1,51 | 1,22 | 0,54 | 1,07 | 184,33 | 10,44 | 90,72 | 6,48 | 22,09 | |||
| 7,65 | 74,10 | 9,28 | 0,26 | 0,74 | 0,27 | 1,46 | 0,68 | 0,75 | 1,44 | 58,42 | 5,65 | 82,44 | 9,72 | 18,29 | |||
| 8,77 | 68,60 | 11,42 | 0,27 | 0,65 | 0,37 | 1,27 | 1,00 | 0,16 | 1,40 | 59,40 | 6,67 | 79,92 | 3,24 | 26,05 | |||
| 7,00 | 60,80 | 10,31 | 0,29 | 0,66 | 0,38 | 1,43 | 0,81 | 0,24 | 1,31 | 49,63 | 5,91 | 120,96 | 6,48 | 26,20 | |||
| 11,06 | 355,60 | 8,65 | 0,01 | 0,84 | 0,35 | 1,50 | 1,27 | 0,59 | 1,12 | 391,27 | 11,99 | 84,60 | 5,40 | 17,26 | |||
| 9,02 | 264,80 | 10,94 | 0,02 | 0,74 | 0,42 | 1,35 | 1,14 | 0,56 | 1,16 | 258,62 | 8,30 | 85,32 | 6,12 | 18,83 | |||
| 13,28 | 526,60 | 9,87 | 0,18 | 0,75 | 0,32 | 1,41 | 1,89 | 0,63 | 0,88 | 75,66 | 1,63 | 101,52 | 8,64 | 19,70 | |||
| 9,27 | 118,60 | 6,14 | 0,25 | 0,75 | 0,33 | 1,47 | 0,67 | 1,10 | 1,07 | 123,68 | 8,94 | 107,64 | 11,88 | 16,87 | |||
| 6,70 | 37,10 | 12,93 | 0,31 | 0,79 | 0,29 | 1,35 | 0,96 | 0,39 | 1,24 | 37,21 | 5,82 | 85,32 | 7,92 | 14,63 | |||
| 6,69 | 57,70 | 9,78 | 0,38 | 0,72 | 0,30 | 1,40 | 0,67 | 0,73 | 1,49 | 53,37 | 4,80 | 131,76 | 10,08 | 22,17 | |||
| 9,42 | 51,60 | 13,22 | 0,24 | 0,70 | 0,56 | 1,20 | 0,98 | 0,28 | 2,03 | 32,87 | 5,01 | 116,64 | 18,72 | 22,62 | |||
| 7,24 | 64,70 | 17,29 | 0,31 | 0,66 | 0,42 | 1,15 | 1,16 | 0,10 | 1,84 | 45,63 | 4,12 | 138,24 | 13,68 | 26,44 | |||
| 5,39 | 48,30 | 7,11 | 0,42 | 0,69 | 0,26 | 1,09 | 0,54 | 0,68 | 1,22 | 48,41 | 5,10 | 156,96 | 16,56 | 22,26 | |||
| 5,61 | 15,00 | 22,49 | 0,51 | 0,71 | 0,16 | 1,26 | 1,23 | 0,87 | 1,72 | 13,58 | 3,49 | 137,52 | 14,76 | 19,13 | |||
| 5,59 | 87,50 | 12,14 | 0,31 | 0,73 | 0,45 | 1,36 | 0,78 | 0,49 | 1,75 | 63,99 | 4,19 | 135,72 | 7,92 | 18,28 | |||
| 6,57 | 108,40 | 15,25 | 0,37 | 0,65 | 0,31 | 1,15 | 1,16 | 0,16 | 1,46 | 104,55 | 5,01 | 155,52 | 18,36 | 28,23 | |||
| 6,54 | 267,30 | 31,34 | 0,16 | 0,82 | 0,08 | 1,87 | 4,44 | 0,85 | 1,60 | 222,11 | 11,44 | 48,60 | 8,28 | 12,39 | |||
| 4,23 | 34,20 | 11,56 | 0,18 | 0,80 | 0,68 | 1,17 | 1,06 | 0,13 | 1,47 | 25,76 | 7,67 | 42,84 | 14,04 | 11,64 | |||
| 5,22 | 26,80 | 30,14 | 0,43 | 0,83 | 0,03 | 1,61 | 2,13 | 0,49 | 1,38 | 29,52 | 4,66 | 142,20 | 16,92 | 8,62 | |||
| 18,00 | 43,60 | 19,71 | 0,40 | 0,70 | 0,02 | 1,34 | 1,21 | 0,09 | 1,41 | 41,99 | 4,30 | 145,80 | 11,16 | 20,10 | |||
| 11,03 | 72,00 | 23,56 | 0,31 | 0,74 | 0,22 | 1,22 | 2,20 | 0,79 | 1,39 | 78,11 | 6,62 | 120,52 | 14,76 | 19,41 |
Примечание: 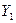 - производительность труда;
- производительность труда; 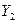 - индекс снижения себестоимости продукции;
- индекс снижения себестоимости продукции; 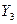 - уровень рентабельности;
- уровень рентабельности; 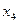 - трудоемкость единицы продукции;
- трудоемкость единицы продукции; 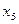 - удельный вес рабочих в составе ППП;
- удельный вес рабочих в составе ППП;  - удельный вес покупных изделий,
- удельный вес покупных изделий, 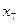 - коэффициент сменности оборудования;
- коэффициент сменности оборудования; 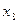 - премии и вознаграждения на одного работника,
- премии и вознаграждения на одного работника, 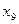 - удельный вес потерь от брака;
- удельный вес потерь от брака; 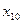 - фондоотдача;
- фондоотдача;  - среднегодовая численность ППП;
- среднегодовая численность ППП; 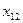 - среднегодовая стоимость ОПФ;
- среднегодовая стоимость ОПФ; 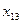 - среднегодовой фонд заработной платы ППП;
- среднегодовой фонд заработной платы ППП; 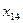 - фондовооруженность труда;
- фондовооруженность труда; 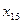 - оборачиваемость нормируемых оборотных средств;
- оборачиваемость нормируемых оборотных средств;  - оборачиваемость ненормируемых оборотных средств;
- оборачиваемость ненормируемых оборотных средств; 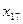 - непроизводственные расходы
- непроизводственные расходы
5.2 Рассмотрим пример построения многофакторной корреляционно-регрессионной модели.
5.3 Рассмотрим влияние на производительность труда рабочих предприятия следующих факторов:
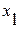 - коэффициент сменности оборудования;
- коэффициент сменности оборудования;
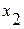 - среднегодовая численность персонала;
- среднегодовая численность персонала;
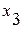 - фондоотдача;
- фондоотдача;
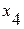 - среднегодовой фонд заработной платы персонала;
- среднегодовой фонд заработной платы персонала;
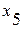 - трудоемкость единицы продукции;
- трудоемкость единицы продукции;
у - производительность труда.
5.4Сбор исходных данных и их первичная обработка.
Для получения статистически значимой модели требуется на один факторный признак объем выборки, равный 5 – 8 наблюдений.
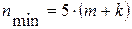 , ,
| (5.1) |
где m - число факторов, включаемых в модель;
k - число свободных членов в уравнении.
Так как в данную модель включены 5 факторов, то минимальный объем выборки равен 30 наблюдениям:

Исходные данные для выполнения многофакторного корреляционно-регрессионного анализа влияния факторов на зависимую переменную собраны в виде динамических рядов и представлены в табл. 5.2.
Таблица 5.2 - Исходные данные
| № наблюдения | Переменные | |||||
| Объясняющие переменные | Зависимая переменная | |||||
| Х 1 | Х 2 | Х 3 | Х 4 | Х 5 | У | |
| 1,35 | 0,91 | 0,23 | 9,35 | |||
| 1,39 | 0,68 | 0,43 | 9,87 | |||
| 1,16 | 0,94 | 0,31 | 8,17 | |||
| 1,27 | 0,89 | 0,26 | 9,12 | |||
| 1,16 | 0,94 | 0,49 | 5,88 | |||
| 1,25 | 2,06 | 0,36 | 6,30 | |||
| 1,13 | 1,96 | 0,37 | 6,22 | |||
| 1,10 | 1,02 | 0,43 | 5,49 | |||
| 1,15 | 1,85 | 0,35 | 6,50 | |||
| 1,23 | 0,88 | 0,38 | 6,61 | |||
| 1,39 | 0,62 | 0,42 | 4,32 | |||
| 1,38 | 1,09 | 0,30 | 7,37 | |||
| 1,35 | 1,60 | 0,32 | 7,02 | |||
| 1,42 | 59,75 | 1,53 | 0,25 | 8,25 | ||
| 1,37 | 1,40 | 0,31 | 8,15 | |||
| 1,41 | 2,22 | 0,26 | 8,72 | |||
| 1,35 | 1,32 | 0,37 | 6,64 | |||
| 1,48 | 1,48 | 0,29 | 8,10 | |||
| 1,24 | 0,68 | 0,34 | 5,52 | |||
| 1,40 | 2,30 | 0,23 | 9,37 | |||
| 1,45 | 1,37 | 0,17 | 13,17 | |||
| 1,40 | 1,51 | 0,29 | 6,67 | |||
| 1,28 | 1,43 | 0,41 | 5,68 | |||
| 1,33 | 1,82 | 0,41 | 5,22 | |||
| 1,22 | 2,62 | 0,22 | 10,02 | |||
| 1,28 | 1,75 | 0,29 | 8,16 | |||
| 1,47 | 1,54 | 0,51 | 3,78 | |||
| 1,27 | 2,25 | 0,36 | 6,48 | |||
| 1,51 | 1,07 | 0,23 | 10,44 | |||
| 1,46 | 1,44 | 0,26 | 7,65 |
5.5 Спецификация функции регрессии.
В нашем примере предполагаем, что имеет место множественная линейная регрессия, т.е. производительность труда линейно зависит от выбранных пяти факторов х1, х2, …, х5. Уравнение регрессии имеет следующий вид:
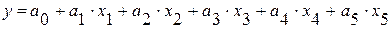
| (5.2) |
где 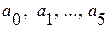 - параметры уравнения регрессии, подлежат оценке.
- параметры уравнения регрессии, подлежат оценке.
5.6 Оценка параметров функции регрессии.
Данный этап выполняется с использованием программного продукта EXCEL. Для этого данные табл. 5.2 необходимо ввести в электронную таблицу EXCEL.
Для выполнения регрессионного и корреляционного анализа в MS EXCEL имеется набор инструментов, называемый Пакет анализа, который может быть использован для решения сложных статистических задач. Порядок действий следующий:
1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис/Надстройки. Установите флажок Пакет анализа.
2) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК
3) заполните диалоговое окно ввода данных и параметров вывода (рис. 5.1):

Рис. 5.1. Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа, выполненного с использованием Пакета анализа, выводятся на экран (рис. 5.2). Уравнение регрессии строится по данным, указанным в графе «Коэффициенты» (ячейки В16:В22). Строка «Y – пересечение» показывает значение свободного члена и соответствующих статистик, строки «х1 – х5» – значения коэффициентов регрессии и соответствующих статистик. Уравнение регрессии имеет вид:

Для данной регрессии коэффициент множественной корреляции равен R = 0,866 (ячейка В4), что свидетельствует о высокой связи между выбранными факторными признаками и производительностью труда рабочих.
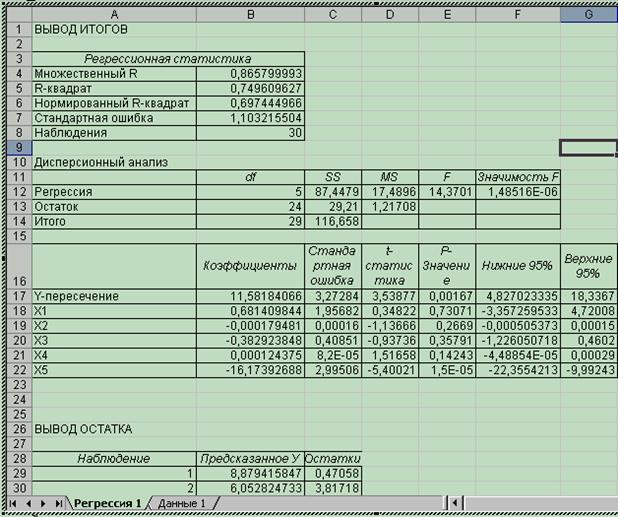
Рис. 5.2. Результаты выполнения функции регрессии
5.7 Отбор главных факторов. Необходимо произвести отбор главных факторов, оказывающих наиболее сильное влияние на функцию Y, т.к. модель, включающая большое количество факторов неустойчива. Неустойчивость модели заключатся в необъективном отражении изменения Y при соответствующих изменениях факторов. Отбор факторов производится на основе анализа значений специальных статистических характеристик.
Процедура отбора главных факторов включает следующие этапы:
5.8 Анализ факторов на мультиколлинеарность и ее исключение.
Определение мультиколлинеарности проводится путем анализа значений коэффициентов парной корреляции 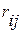 между факторами
между факторами  и
и 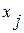 . Если
. Если 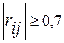 , то факторы
, то факторы  и
и 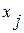 мультиколлинеарны.
мультиколлинеарны.
Для получения коэффициентов парной корреляции необходимо вычислить корреляционную матрицу. Для этого:
1) вернуться на лист «Данные 1»;
2) в главном меню выберите Сервис/Анализ данных/Корреляция. Щелкните по кнопке ОК.
3) заполните диалоговое окно ввода данных и параметров вывода (рис. 5.3):

Рис. 5.3. Диалоговое окно ввода параметров инструмента Корреляция
Результаты корреляционного анализа представлены на рис. 5.4.

Рис. 5.4 Корреляционная матрица
В рассматриваемом примере мультиколлинеарность присутствует между факторами х2 и х4 (коэффициент парной корреляции между ними равен 0,989).
Для устранения мультиколлинеарности один из факторов необходимо исключить из модели. Факторы, подлежащие исключению, определяются в ходе оценки следующих статистических характеристик: коэффициента парной корреляции между факторным и результативным признаками 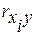 ; коэффициента β; критерия Стьюдента.
; коэффициента β; критерия Стьюдента.
5.9 Анализ тесноты взаимосвязи факторов (х) с зависимой переменной (у). Для анализа тесноты взаимосвязи х и у используются значения коэффициента парной корреляции между фактором и функцией (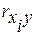 ), представленные в последней строке корреляционной матрицы.
), представленные в последней строке корреляционной матрицы.
Факторы, для которых 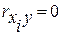 , т.е. не связанные с
, т.е. не связанные с 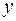 , подлежат исключению в первую очередь. Факторы, имеющие наименьшее значение
, подлежат исключению в первую очередь. Факторы, имеющие наименьшее значение 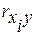 , могут быть потенциально исключены из модели. В данном примере фактор Х2 мультиколлинеарный с фактором Х4 в меньшей степени связан с результативным признаком (
, могут быть потенциально исключены из модели. В данном примере фактор Х2 мультиколлинеарный с фактором Х4 в меньшей степени связан с результативным признаком (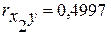 ), поэтому этот фактор потенциально исключается из модели.
), поэтому этот фактор потенциально исключается из модели.
Фактор Х3 необходимо исключить из модели, так как коэффициент парной корреляции между этим фактором и результативным признаком близок к нулю ( ).
).
Вопрос об их окончательном исключении решается в ходе анализа других статистических характеристик.
5.10 Анализ факторов на управляемость. В ходе логического анализа на основе экономических знаний исследователь должен сделать вывод: можно ли разработать организационно - технические мероприятия, направленные на улучшение (изменение) выбранных факторов на уровне предприятия. Если это возможно, то данные факторы управляемы. Неуправляемые факторы на уровне предприятия могут быть исключены из модели. В данном случае все факторы являются управляемыми на уровне предприятия.
5.11 Проверка коэффициентов регрессии на статистическую значимость. Проверка может быть произведена двумя способами: по критерию Стьюдента и по критерию Фишера.
В данном примере остановимся на проверке статистической значимости коэффициентов регрессии по критерию Стьюдента:
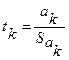 , ,
| (5.3) |
где  - коэффициент регрессии при
- коэффициент регрессии при 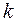 -ом факторе;
-ом факторе;
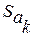 - стандартное отклонение оценки параметра
- стандартное отклонение оценки параметра  .
.
Критерий Стьюдента уже был вычислен при выполнении регрессионного анализа (см. Лист «Регрессия 1», столбец «t – статистика», рис. 5.2).
Число степеней свободы статистики  равно
равно  , где n - количество наблюдений,
, где n - количество наблюдений,  - количество факторов, включенных в модель. Расчетное значение показателя
- количество факторов, включенных в модель. Расчетное значение показателя  ,сравнивают с критическим значением, найденным по табл. 5.3.
,сравнивают с критическим значением, найденным по табл. 5.3.
Таблица 5.3 - Критические значения t – критерия Стьюдента при уровне значимости 0,10; 0,05; и 0,01
| Число степеней свободы d.f. | a | Число степеней свободы d.f. | a | ||||
| 0.10 | 0.05 | 0.01 | 0.10 | 0.05 | 0.01 | ||
| 6.313752 | 12.70620 | 31.82052 | 1.734064 | 2.10092 | 2.55238 | ||
| 2.919986 | 4.30265 | 6.96456 | 1.729133 | 2.09302 | 2.53948 | ||
| 2.353363 | 3.18245 | 4.54070 | 1.724718 | 2.08596 | 2.52798 | ||
| 2.131847 | 2.77645 | 3.74695 | 1.720743 | 2.07961 | 2.51765 | ||
| 2.015048 | 2.57058 | 3.36493 | 1.717144 | 2.07387 | 2.50832 | ||
| 1.943180 | 2.44691 | 3.14267 | 1.713872 | 2.06866 | 2.49987 | ||
| 1.894579 | 2.36462 | 2.99795 | 1.710882 | 2.06390 | 2.49216 | ||
| 1.859548 | 2.30600 | 2.89646 | 1.708141 | 2.05954 | 2.48511 | ||
| 1.833113 | 2.26216 | 2.82144 | 1.705618 | 2.05553 | 2.47863 | ||
| 1.812461 | 2.22814 | 2.76377 | 1.703288 | 2.05183 | 2.47266 | ||
| 1.795885 | 2.20099 | 2.71808 | 1.701131 | 2.04841 | 2.46714 | ||
| 1.782288 | 2.17881 | 2.68100 | 1.699127 | 2.04523 | 2.46202 | ||
| 1.770933 | 2.16037 | 2.65031 | 1.697261 | 2.04227 | 2.45726 | ||
| 1.761310 | 2.14479 | 2.62449 | 40. | 1,6839 | 2,0211 | 2,7045 | |
| 1.753050 | 2.13145 | 2.60248 | 60. | 1,6707 | 2,0003 | 2,6603 | |
| 1.745884 | 2.11991 | 2.58349 | 120. | 1,6577 | 1,9799 | 2,6174 | |
| 1.739607 | 2.10982 | 2.56693 | inf | 1.644854 | 1.95996 | 2.32635 |
При заданном уровне значимости α = 0,05 и числе степеней свободы 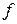 = 30 – 5 – 1 = 24, в данном примере
= 30 – 5 – 1 = 24, в данном примере 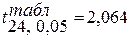 .
.
Так как все значения 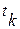 удовлетворяют неравенству
удовлетворяют неравенству 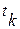 <
<  (за исключением х5), следовательно, влияние выбранных факторов на зависимую переменную статистически незначимо и полученную регрессионную модель можно использовать только для текущего анализа.
(за исключением х5), следовательно, влияние выбранных факторов на зависимую переменную статистически незначимо и полученную регрессионную модель можно использовать только для текущего анализа.
5.12 Анализ коэффициентов 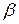 факторов. Для того, чтобы определить, какие факторы подлежат исключению проведем анализ коэффициентов
факторов. Для того, чтобы определить, какие факторы подлежат исключению проведем анализ коэффициентов 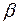 факторов.
факторов.
Коэффициент 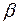 показывает влияние анализируемых факторов на результативный признак с учетом различий в уровне их колеблемости:
показывает влияние анализируемых факторов на результативный признак с учетом различий в уровне их колеблемости:
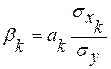 , ,
| (5.4) |
где - коэффициент 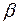
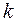 -го фактора;
-го фактора;
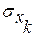 - среднеквадратическое отклонение
- среднеквадратическое отклонение 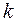 - го фактора;
- го фактора;
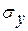 - среднеквадратическое отклонение функции;
- среднеквадратическое отклонение функции;
 - коэффициент регрессии при
- коэффициент регрессии при 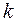 -ом факторе.
-ом факторе.
Из двух факторов  и
и 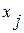 может быть исключен тот фактор, который имеет меньшее значение
может быть исключен тот фактор, который имеет меньшее значение 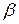 .
.
5.13 Для расчета коэффициентов  предварительно необходимо рассчитать среднеквадратическое отклонение (рис. 5.5).
предварительно необходимо рассчитать среднеквадратическое отклонение (рис. 5.5).
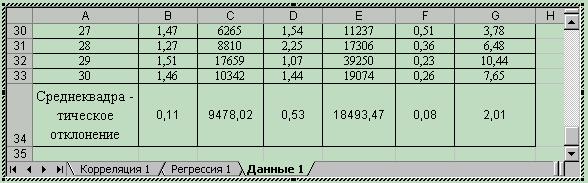
Рис. 5.5 Расчет среднеквадратического отклонения
5.14 На листе «Корреляция 1» создайте таблицу для расчета коэффициентов  . В столбце А разместите результативный признак Y и мультколлинеарные факторы х2 и х4. В столбец В - коэффициенты
. В столбце А разместите результативный признак Y и мультколлинеарные факторы х2 и х4. В столбец В - коэффициенты  , которые скопируйте с листа «Регрессия1». В столбец С необходимо скопировать среднеквадратическое отклонение с листа «Данные 1».
, которые скопируйте с листа «Регрессия1». В столбец С необходимо скопировать среднеквадратическое отклонение с листа «Данные 1».
5.15 В ячейку D14 необходимо ввести формулу для расчета коэффициента  .
.
Результаты расчета коэффициентов 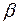 представлены на рис. 5.5.
представлены на рис. 5.5.
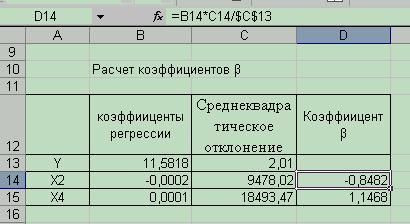
Рис. 5.5 Результаты расчета коэффициента 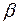
Из двух факторов  и
и 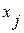 может быть исключен тот фактор, который имеет меньшее значение коэффициента
может быть исключен тот фактор, который имеет меньшее значение коэффициента 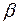 . Следовательно, исключить необходимо фактор х2.
. Следовательно, исключить необходимо фактор х2.
5.16 Построение новой регрессионной модели без исключенных факторов. После исключения факторных признаков х2 и х3 таблица исходных данных должна быть преобразована следующим образом (рис. 5.6):


Рис. 5.6 Фрагмент листа «Данные 2»
5.17 для новых исходных данных выполните функции «Регрессия» и «Корреляция»;
5.18 переименуйте листы с полученными результатами соответственно «Регрессия 2» и «Корреляция 2».
5.19 Исследование целесообразности исключения факторов из модели с помощью коэффициента детерминации. Прежде чем вынести окончательное решение об исключении переменных из анализа в силу их незначимого влияния на зависимую переменную, производят исследования совместного влияния факторов.
Для этого используется статистика, которая имеет F – распределение со степенями свободы 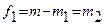 и
и 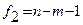 :
:
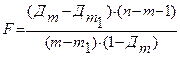 , ,
| (5.5) |
где  - означает коэффициент детерминации регрессии с
- означает коэффициент детерминации регрессии с 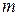 объясняющими переменными,
объясняющими переменными,
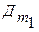 - коэффициент детерминации регрессии с
- коэффициент детерминации регрессии с 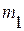 - факторами,
- факторами,
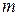 - число переменных в первой регрессии;
- число переменных в первой регрессии;
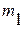 - число переменных во второй регрессии.
- число переменных во второй регрессии.
5.20 Расчетное значение необходимо сравнить с критическое значение  , найденным по специальным таблицам при заданном уровне значимости
, найденным по специальным таблицам при заданном уровне значимости  и степенях свободы
и степенях свободы 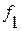 и
и 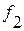 .
.
Если 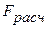 ≤
≤ 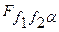 , то включение дополнительно объясняющих переменных совместно не оказывает значимого влияния на переменную
, то включение дополнительно объясняющих переменных совместно не оказывает значимого влияния на переменную 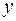 и факторы окончательно исключаются из модели.
и факторы окончательно исключаются из модели.
Если 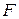 >
> 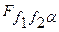 , то исключенные объясняющих переменных совместно оказывают существенное влияние на вариацию переменной y и, следовательно, в этом случае все переменные нельзя исключать из модели.
, то исключенные объясняющих переменных совместно оказывают существенное влияние на вариацию переменной y и, следовательно, в этом случае все переменные нельзя исключать из модели.
5.21 Вычислим 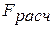 :
:
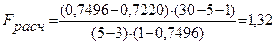 .
.
5.22 Определим критическое значение статистики F при 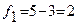 и
и  и уровне значимости α = 0,05:
и уровне значимости α = 0,05: 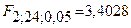 , с помощью таблицы П.3.1.
, с помощью таблицы П.3.1.
Так как 1,32<3,40, следовательно, ранее исключенные факторы 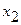 и
и 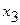 совместно не оказывают статистически значимого влияния на переменную у.
совместно не оказывают статистически значимого влияния на переменную у.
5.23 Проверка адекватности модели.
Данный этап анализа включает:
а) оценку значимости коэффициента детерминации, т.е. оценивается влияние выбранных факторов на зависимую переменную, она производится с помощью статистики:
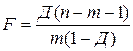 , ,
| (5.6) |
где Д – коэффициент множественной детерминации (второй регрессии).
Расчетное значение статистики F, вычисленное по эмпирическим данным, сравнивается с табличным значением, которое определяется по табл. П.3.1, при заданном уровне значимости  и степенях свободы:
и степенях свободы: 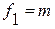 и
и 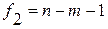 .
.
В нашем случае имеем 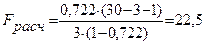 .
.
Табличное значение F – статистики равно: 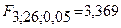 при
при  и
и 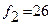 и α = 0,05.
и α = 0,05.
Так как 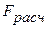 ≥
≥ 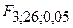 , то вычисленный коэффициент детерминации значимо отличается от 0 и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную, что позволяет говорить о значимости самой регрессии (модели);
, то вычисленный коэффициент детерминации значимо отличается от 0 и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную, что позволяет говорить о значимости самой регрессии (модели);
б) проверку качества подбора теоретического уравнения с использованием средней ошибки аппроксимации:
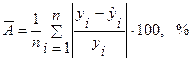 , ,
| (5.7) |
где 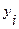 - фактическое значение результативного признака для i -го наблюдения
- фактическое значение результативного признака для i -го наблюдения
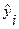 - теоретическое значение результативного признака для i -го наблюдения, вычисленное по уравнению множественной регрессии;
- теоретическое значение результативного признака для i -го наблюдения, вычисленное по уравнению множественной регрессии;
5.24 Вычисления средней ошибки аппроксимации происходит следующим образом:
1) на листе «Регрессия 2» в ячейку D26 введите заголовок «Фактическое Y», в ячейку Е26 – «Составляющие для ошибки»;
2) с листа «Данные 2» скопируйте на лист «Регрессия 2» фактические значения результативного признака:
а) на листе «Данные 2» выделите диапазон ячеек Е4:Е33 и нажмите кнопку «Копировать» на панели Стандартная;
б) на листе «Регрессия 2» выделите ячейки D27:D56 и нажмите кнопку «Вставить»;
3) в ячейку Е27 введите формулу для расчета.
4) в ячейку D57 введите «Средняя ошибка»;
5) для вычисления средней ошибки аппроксимации регрессии необходимо воспользоваться формулой вычисления среднего значения.
Результаты расчета средней ошибки аппроксимации представлены на рис. 5.7.

Рис. 5.7 Результаты расчета средней ошибки аппроксимации
В нашем примере ошибка аппроксимации превышает допустимое значение (8 – 10 %), что свидетельствует о недостаточно высоком уровне качества подбора уравнения регрессии. Следовательно, полученное уравнение регрессии можно использовать только для текущего анализа.
5.25 Исходя из всех вышеперечисленных расчетов, используя коэффициенты регрессии (лист «Регрессия 2»), запишем корреляционно-регрессионное уравнение производительности труда:
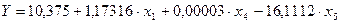 .
.
5.26 Вывод.
В ходе корреляционно-регрессионного анализа было выявлено, что главными факторами определяющими вариацию уровня производительности труда работников промышленного предприятия в ретроспективном периоде являются: коэффициент сменности оборудования, фонд оплаты труда рабочих и трудоемкость единицы продукции. Очевидно, в будущем периоде для повышения производительности труда, необходимо, прежде всего, уделить особое внимание на снижении трудоемкости изготовления продукции предприятия.
Содержание отчета и его форма
Отчет должен содержать:
6.1 Постановку экономической проблемы и ее качественный анализ
6.2 Формирование перечня факторов и их логический анализ.
6.3 Сбор исходных данных и их первичная обработка.
6.4 Спецификацию функции регрессии.
6.5 Оценку параметров функции регрессии.
6.6 Отбор главных факторов.
6.7 Проверку адекватности модели.
6.8 Экономическую интерпретация.
6.9 Прогнозирование неизвестных значений зависимой переменной.
6.10 Выводы.
Контрольные вопросы и защита работы
7.1 Общий вид уравнения множественной регрессии.
7.2 Этапы построения многофакторной корреляционно-регрессионной модели.
7.3 Что в себя включает априорное исследование и постановка экономической проблемы.
7.4 Каким образом производится оценка параметров функции регрессии.
7.5 Методика отбора главных факторов.
Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы представленных выше.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА






