При проведении научных исследований, в основе которых лежит активный эксперимент, на первом этапе происходит описание эксперимента, и формируется его цель. Выбирается целевая функция, которая является обобщенным показателем качества исследуемого процесса или явления. Например, при исследовании топливной экономичности автомобиля целевой функцией может быть часовой расход или удельный расход топлива и т.п.
Далее определяются основные факторы, оказывающие влияние на целевую функцию, и границы их измерения.
Например, на топливную экономичность автомобиля оказывает влияние:
· техническое состояние системы питания, которое может характеризоваться уровнем топлива в поплавковой камере карбюратора, пропускной способностью жиклеров, давлением нагнетания и всасывания бензонасоса;
· техническим состоянием системы зажигания, характеризующимся следующими факторами: углом опережения зажигания, углом замкнутого состояния контактов прерывателя, зазором в свече зажигания и и.д.;
· техническим состоянием ходовой части и трансмиссии автомобиля (давление воздуха в шинах, люфты в трансмиссии и т.д.);
· техническое состояние двигателя (величина давления в конце такта сжатия, зазор в клапанах и т.д.).
При выборе факторов, предпочтение отдается наиболее влияющим на целевую функцию. При этом используют метод экспертных оценок, метод случайного баланса, корреляционно-регрессионного анализа.
При планировании эксперимента различают понятие полнофакторного эксперимента и понятие дробной реплики.
Если все уровни каждого фактора сочетаются со всеми уровнями остальных факторов, то такой эксперимент называют полнофакторным. Для него число опытных точек определяется по формуле:
n = ak , (1)
где а — число уровней каждого фактора;
k — число факторов эксперимента.
Для повышения точности эксперимента проводят в каждой точке по несколько параллельных опытов - r.
Таким образом, общее число наблюдений составит:
N’ = n×r. (2)
Совокупность уровней факторов образует факторное пространство. Сочетание уровней факторов отражает матрица планирования эксперимента. Она представляет собой таблицу, в которой содержится как информация о сочетании уровней факторов в каждом эксперименте, так и данные для статистического анализа результатов эксперимента. Информация в матрицу обычно вводится в кодированном виде. Значения уровней факторов в кодированном виде (xik) определяется по формуле
 (3)
(3)
где хji — j-й уровень фактора;
х0i — основной уровень фактора;
хвi — верхний уровень фактора;
хнi — нижний уровень фактора.
Например. Нормальный зазор впускных и выпускных клапанов двигателя внутреннего сгорания составляет 0,2 мм. В процессе эксплуатации двигателя зазор в клапанах изменяется в пределах (0,1- 0,3) мм. Проведем кодирование уровней данного фактора.
Для верхнего уровня
 .
.
Для нижнего уровня
 .
.
Полно-факторный эксперимент несет значительную избыточность числа проводимых опытов. Это удорожает эксперимент, делает его громоздким, длительны и т.д.
Избыточность плана определяется по формуле:
D и = ак - (к+1). (4)
Каждый эксперимент в матрице планирования принято обозначать буквой латинского алфавита. Например, если фактор х1 находится на верхнем уровне, то а, если фактор х2 находится на верхнем уровне, то b и т.д. Эффект взаимодействия факторов, находящихся на верхнем уровне, обозначается произведением соответствующих букв. Например, если факторы х1 и х2 находятся на верхнем уровне, то эксперимент обозначают через а×b и т.д. Эксперимент обозначают единицей (I), если все факторы находятся на нижнем уровне.
Если планирование ведется на 2-х уровнях, то кодированные значения уровней аргументов будет равняться или +1 или -1. На практике их заменяют “плюсом” и “минусом” соответственно.
Множество точек хi, в которых производятся наблюдения, и соответствующее число наблюдений в этих точках называют планом эксперимента.
Если все факторы имеют одинаковое число уровней, то план называется симметричным.
Пример заполнения матрицы планирования эксперимента для трехфакторного двухуровневого эксперимента без взаимодействия представлен в таблице 1. Модель эксперимента имеет следующий вид:
 . (5)
. (5)
Для вычисления свободного члена b0 в уравнениях регрессии необходимо в матрицу ввести вектор-столбец фиктивного фактора х0, который имел бы во всех опытах значение (+1).
Таблица 1 - План эксперимента
| Номер эксперимента | х0 | Матрица планирования | Условное обозначение | У | ||
| х1 | х2 | х3 | ||||
| + | - | - | - | (I) | y1 | |
| + | + | - | - | a | y2 | |
| + | - | + | - | b | y3 | |
| + | + | + | - | ab | y4 | |
| + | - | - | + | c | y5 | |
| + | + | - | + | ac | y6 | |
| + | - | + | + | bc | y7 | |
| + | + | + | + | abc | y8 |
Выбирается вид математической модели, с помощью которой предполагается описать исследуемый процесс. Как правило, вид модели устанавливают, используя априорную информацию. Если же она не дает представлений о характере поверхности отклика, то выбор вида модели осуществляется шаговым поиском. При этом первоначально поверхность отклика полагается линейной и аппроксимируеся моделью вида
 . (6)
. (6)
Если полученная модель неадекватна исследуемому процессу, то она расширяется путем включения эффектов взаимодействия первого порядка
 . (7)
. (7)
Если же и эта модель неадекватна, то добавляют экспериментальные точки для получения квадратичной модели
 . (8)
. (8)
Определение коэффициентов линейной многофакторной модели могут применяться два способа:
Ø Способ, основанный на составлении и решении нормальных уравнений;
Ø Способ, основанный на применении матричного исчисления.
Используя первый способ, значения коэффициентов регрессии определяем по формулам:
- свободного члена
 ; (9)
; (9)
- линейных коэффициентов
 ; (10)
; (10)
- коэффициентов характеризующих парное взаимодействие
 . (11)
. (11)
Используя второй способ необходимо найти информационную матрицу (ХТХ) и матрицу ошибок (ХТХ)-1. При этом ХТ - транспонированная матрица, т.е. если в заданной матрице Х заменить строки столбцами, то в этом случае получается транспонированная матрица. Например, если
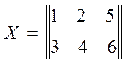 , то
, то 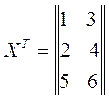 .
.
Перемножение матриц производится по определенному правилу. Для этого, элементы каждой из строк первой матрицы последовательно умножаются на элементы соответствующего столбца другой матрицы и результаты перемножения складываются.
Например, если заданы 2 матрицы:
 и
и  ,
,
то  .
.
Выражение для вычисления матричным способом коэффициентов математической модели по методу наименьших квадратов имеет следующий вид:







