Проверка воспроизводимости эксперимента

После произведения опытов необходимо производить проверку воспроизводимости эксперимента. Проверку необходимо проводить потому, что при фиксировании наблюдаемых значений функции отклика в различных точках факторного пространства могут возникать ошибки, например, ошибки эксперимента, ошибки отсчета по шкалам приборов, ошибки от влияния неучтенных и неуправляемых факторов и т.п. Значения указанных ошибок характеризуются отвечающими им в различных точках построчными дисперсиями:

 

S²{y₁}, S²{y₂},.....S²{y_n}.

Если построчные дисперсии в различных точках факторного пространства мало отличаются друг от друга, то говорят, что дисперсии однородны и имеет место хорошая воспроизводимость эксперимента. В противном случае говорят, что дисперсии неоднородны.

Простым и удобным способом проверки однородности дисперсии эксперимента является критерий Кохрена. Опытное значение критерия Кохрена определяется по формуле:

 

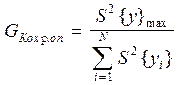, (12)

 

где G_{кахр.оп} — опытное значение критерия Кохрена;

G_{кахр.табл} — табличное значение критерия Кохрена (таблица 2);

S²{y₁ } _max — максимальное значение построчной дисперсии;

²{y₁ } —сумма построчных дисперсий;

a — уровень значимости;

k = r-1 - число степеней свободы;

r — число параллельных опытов;

N — число рассматриваемых дисперсий.

 

Если G_{кахр.оп} £ G_{кахр.табл -} гипотеза об однородности дисперсий не отвергается;

если G_{кахр.оп} >G_{кахр.табл -} гипотеза об однородности дисперсий отвергается;

 

Таблица 2 — Табличные значения критерия Кохрена G_табл,

вычисленные в зависимости от числа степеней свободы k = r—1 и числа испытаний n при уровне значимости a=0,05

Уровень значимости a=0,05
n	k
1	2	3	4	5	6	7	8	8	10
	0,97	0,93	0,90	0,87	0,85	0,81	0,78	0,73	0,66
	0,93	0,79	0,74	0,70	0,66	0,63	0,60	0,54	0,47
	0,76	0,68	0,62	0,59	0,56	0,51	0,48	0,43	0,36
	0,68	0,60	0,54	0,50	0,48	0,44	0,41	0,36	0,30
	0,61	0,53	0,48	0,44	0,42	0,38	0,35	0,31	0,25
	0,56	0,48	0,43	0,39	0,37	0,34	0,31	0,27	0,23
	0,51	0,43	0,39	0,36	0,33	0,30	0,28	0,24	0,20
	0,47	0,40	0,35	0,33	0,30	0,28	0,25	0,22	0,18
	0,44	0,37	0,33	0,30	0,28	0,25	0,23	0,20	0,16
	0,39	0,32	0,29	0,26	0,24	0,22	0,20	0,17	0,14
	0,33	0,27	0,24	0,22	0,20	0,18	0,17	0,14	0,11
	0,27	0,22	0,19	0,17	0,16	0,14	0,13	0,11	0,08
	0,23	0,19	0,16	0,15	0,14	0,12	0,11	0,09	0,07
	0,20	0,16	0,14	0,12	0,11	0,10	0,09	0,07	0,06
	0,16	0,12	0,10	0,09	0,08	0,07	0,07	0,06	0,04
	0,11	0,08	0,07	0,06	0,06	0,05	0,05	0,04	0,02
	0,06	0,04	0,04	0,03	0,03	0,02	0,02	0,02	0,01

 

 

Статистическая оценка значимости коэффициентов математической модели

 

Статистическая оценка значимости коэффициентов математической модели производится с помощью критерия Стьюдента, согласно следующему альтернативному условию:

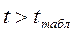— коэффициент значим

 

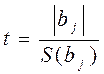; (13)

 

; (14)

 

где S²(b_j) – дисперсия коэффициентов модели;

S² (у) – дисперсия эксперимента.

 

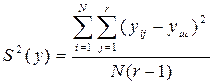. (15)

 

Табличное значение критерия Стьюдента выбирается в зависимости от уровня значимости a=0,05 и числа степеней свободы к = N—1 из таблицы 3

 

Таблица 3 - Табличные значения критерия Стьюдента t_табл(a; k), вычисленные в зависимости от числа степеней свободы k=N—1 при заданном уровне значимости a

 

k	Уровень значимости a
0,1	0,05	0,01
	6.31	12.71	63.66
	2.92	4.3	9.93
	2.35	3.18	5.84
	2.13	2.78	4.6
	2.02	2.57	4.03
	1.94	2.45	3.71
	1.90	2.37	3.5
	1.86	2.31	3.36
	1.83	2.26	3.25
	1.81	2.23	3.11
	1.75	2.13	2.95
	1.73	2.09	2.85
	1.7	2.02	2.75
	1.68	2.02	2.7
	1.67	2.00	2.66
	1.66	1.98	2.62
¥	1.65	1.96	2.58