При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.
Методика и порядок выполнения работы
5.1 Определить координаты кривых в системе ограничений.
5.2 Графически представить ограничения.
5.3 Определить оптимальную структуру цикла светофорного регулирования.
Содержание отчета и его форма
Отчет должен содержать:
6.1 Расчет координат кривых в системе ограничений.
6.2 График ограничений.
6.3 Расчет оптимальной структуры цикла светофорного регулирования.
6.4 Выводы.
Контрольные вопросы и защита работы
7.1 Каково минимальное значение основного такта?
7.2 Каково максимальное значение цикла регулирования?
7.3 Что такое целевая функция?
7.4 Какова целевая функция?
7.5 К чему сводится решение задачи оптимизации циклов светофорного регулирования?
Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.
Практическое занятие 23
Корреляционно-регрессионный анализ. расчет параметров уравнений
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Регрессия – это односторонняя вероятностная зависимость между случайными переменными.
Уравнение простой регрессии характеризует вероятностную связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений
, (1)
где у – зависимая переменная (результативный признак);
х – независимая, или объясняющая, переменная (признак – фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия:
у=а+bх+ε, (2)
где а – свободный член уравнения,
b – коэффициент регрессии,
ε – случайная величина, характеризующая отклонение реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Нелинейные регрессии делятся на два класса:
- регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам,
- регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
1) полиномы разных степеней: у = а + b1 x + b2 x2 + b3 x3 + … + bnxn + e
2) равносторонняя гипербола: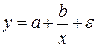 
Регрессии, нелинейные по оценивающим параметрам:
1) степенная: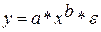 
2) экспоненциальная: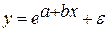 
3) показательная: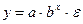 
Построение уравнения парной регрессии сводится к оценке ее параметров. Наиболее часто для этого применяется метод наименьших квадратов (МНК), который позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических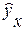 
минимальна, т.е. 
.
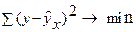В парной регрессии выбор вида математической функции (2.1) может быть осуществлен тремя методами:
- графическим;
- аналитическим;
- экспериментальным.
При изучении зависимости между двумя признаками графический метод подбора вида уравнения достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 2.1.
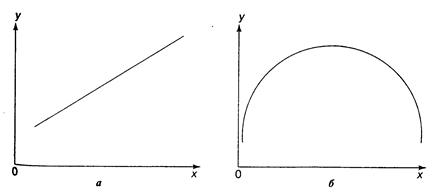
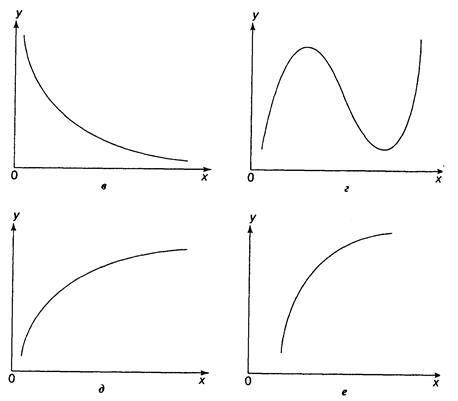
Рис. 1 Основные типы кривых, используемые при количественной оценке связей между двумя переменными:
а) у=а+bх б) у=а+bx+cx2
в) у=а+b/х г) у=а+bx+cx2+dx3
д) у=а*хb е) у=а*bx
Аналитический метод основан на изучении материальной природы связи исследуемых признаков. Например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х. Все потребление электроэнергии у можно подразделить на две части:
· не связанные с производством продукции а;
· непосредственно связанные с объемом выпускаемой продукции, пропорционально возрастающие с увеличением объема выпуска (b∙х).
Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида
 =а+bх.
| (3) |
При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т.е. путем сравнения величины остаточной дисперсии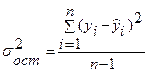 
рассчитанной при разных моделях. Чем меньше величина остаточной дисперсии, тем меньше влияние неучтенных в модели факторов на результативный и лучше уравнение регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции из них выбирается та, для которой дисперсия является наименьшей.
Пример
1Расчет произведен на примере объема продукции предприятия от среднегодовой стоимости ОПФ (таблица 5.1).
2 В качестве наглядного примера рассмотрим зависимость потребительских расходов на душу населения от денежные доходов (табл. 2).
Таблица 2 - Исходные данные
| № п/п | Район | Потребительские расходы на душу населения, тыс. руб. | Денежные доходы на душу населения, тыс. руб. |
| Восточно-Сибирский | |||
| Республика Бурятия | |||
| Республика Тыва | |||
| Республика Хакасия | |||
| Красноярский край | |||
| Иркутская область | |||
| Усть-Ордынский Бурятский авт. округ | |||
| Читинская область | |||
| Дальневосточный | |||
| Республика Саха (Якутия) | |||
| Еврейская автономная область | |||
| Чукотский автономный округ | |||
| Приморский край | |||
| Хабаровский край | |||
| Амурская область | |||
| Камчатская область | |||
| Магаданская область | |||
| Сахалинская область |
3 Определить факторный и результативный признаки. Так как расходы населения зависят от их доходов, то факторным признаком x (тыс. руб.) будет денежные доходы на душу населения, а потребительские расходы на душу населения – результативным y (тыс. руб.).
4 Построить поле корреляции. Поле корреляции, характеризующее зависимость расходов населения от их денежных доходов, представлено на рис. 1.
5 Сделать предварительный вывод о функции тренда. Анализируя поле корреляции, можно предположить, что между изучаемыми переменными существует линейная или степенная зависимости.
Рис. 1 - Поле корреляции
6 Рассчитать параметры линейной регрессии. Для расчета параметров а и b линейной регрессии y = a + bx необходимо решить систему нормальных уравнений относительно a и b:
 .
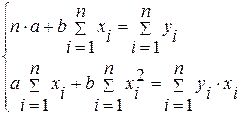| (1) |
Для расчета можно воспользоваться готовыми формулами:
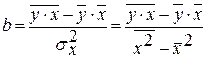
| (2) |
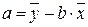
| (3) |
7 Промежуточные расчеты представить в таблице (таблица 3).
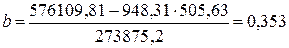
Уравнение регрессии: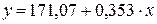 
. Следовательно, с увеличением доходов на 1 тыс. руб. расходы возрастают в среднем на 0,353 тыс. руб.
Таблица 3 – Оценка параметров линейного уравнения регрессии
| № п/п |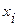 
| 
| 
| 
| 
| 
| 
| 
|
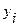
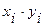
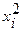
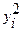
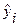
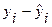
| 355,9 | 52,1 | 0,13 | ||||||
| 302,0 | -53,0 | 0,21 | ||||||
| 330,9 | -77,9 | 0,31 | ||||||
| 529,5 | 50,5 | 0,09 | ||||||
| 522,8 | 128,2 | 0,20 | ||||||
| 247,6 | -108,6 | 0,78 | ||||||
| 342,5 | -20,5 | 0,06 | ||||||
| 872,8 | 26,2 | 0,03 | ||||||
| 381,0 | -51,0 | 0,15 | ||||||
| 717,9 | -271,9 | 0,61 | ||||||
| 501,6 | 140,4 | 0,22 | ||||||
| 439,5 | 102,5 | 0,19 | ||||||
| 441,7 | 62,3 | 0,12 | ||||||
| 777,9 | 83,1 | 0,10 | ||||||
| 784,2 | -77,2 | 0,11 | ||||||
| 542,2 | 14,8 | 0,03 | ||||||
| Итого | х | 0,0 | 3,33 | |||||
| Среднее значение | 948,31 | 505,63 | 576109,81 | 1173171,8 | 300191,25 | х | х | 0,208 |
| Дисперсия | 273875,2 | 44534,6 | х | х | х | х | х | х |
| СКО | 523,33 | 211,03 | х | х | х | х | х | х |
8 Построить степенную модель. Построению степенной модели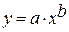 
предшествует процедура линеаризации переменных. Линеаризацию можно провести путем логарифмирования обеих частей уравнения:
 ;
| (4) |
 .
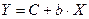| (5) |
где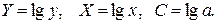 
9 Результаты расчетов представить в таблице (таблица 5.4).
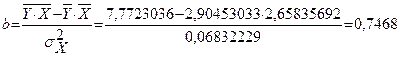
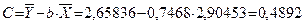
Таблица 4 – Оценка параметров степенной модели
| № п/п |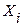 
| 
| 
| 
| 
|
|
|
|
| 
| 
| 
|
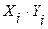
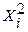
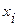
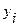
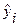
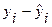
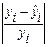
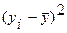
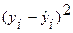
| 2,7193 | 2,6107 | 7,0992 | 7,3948 | 6,8155 | 331,1 | 76,9 | 0,19 | 9530,6 | 5914,31 | |||
| 2,5694 | 2,3962 | 6,1567 | 6,6017 | 5,7418 | 255,8 | -6,8 | 0,03 | 65856,4 | 46,76 | |||
| 2,6561 | 2,4031 | 6,3829 | 7,0549 | 5,7750 | 297,0 | -44,0 | 0,17 | 63819,4 | 1934,45 | |||
| 3,0069 | 2,7634 | 8,3093 | 9,0414 | 7,6365 | 542,9 | 37,1 | 0,06 | 5531,6 | 1377,80 | |||
| 2,9987 | 2,8136 | 8,4371 | 8,9922 | 7,9162 | 535,3 | 115,7 | 0,18 | 21133,9 | 13390,79 | |||
| 2,3365 | 2,1430 | 5,0071 | 5,4590 | 4,5925 | 171,4 | -32,4 | 0,23 | 134413,9 | 1050,12 | |||
| 2,6866 | 2,5079 | 6,7377 | 7,2180 | 6,2893 | 313,0 | 9,0 | 0,03 | 33718,1 | 81,10 | |||
| 3,2986 | 2,9538 | 9,7434 | 10,8810 | 8,7247 | 896,6 | 2,4 | 0,00 | 154743,9 | 5,98 | |||
| 2,7745 | 2,5185 | 6,9877 | 7,6979 | 6,3429 | 364,1 | -34,1 | 0,10 | 30844,1 | 1159,68 | |||
| 3,1903 | 2,6493 | 8,4523 | 10,1782 | 7,0190 | 744,2 | -298,2 | 0,67 | 3555,1 | 88930,05 | |||
| 2,9717 | 2,8075 | 8,3433 | 8,8312 | 7,8823 | 511,0 | 131,0 | 0,20 | 18598,1 | 17151,49 | |||
| 2,8814 | 2,7340 | 7,8777 | 8,3024 | 7,4748 | 437,5 | 104,5 | 0,19 | 1323,1 | 10920,96 | |||
| 2,8848 | 2,7024 | 7,7960 | 8,3220 | 7,3031 | 440,1 | 63,9 | 0,13 | 2,6 | 4087,04 | |||
| 3,2355 | 2,9350 | 9,4963 | 10,4686 | 8,6142 | 804,4 | 56,6 | 0,07 | 126291,4 | 3208,34 | |||
| 3,2400 | 2,8494 | 9,2323 | 10,4979 | 8,1192 | 810,6 | -103,6 | 0,15 | 40551,9 | 10740,38 | |||
| 3,0220 | 2,7459 | 8,2980 | 9,1326 | 7,5397 | 557,2 | -0,2 | 0,00 | 2639,4 | 0,03 | |||
| Итого | 46,4725 | 42,5337 | 124,3569 | 136,0739 | 113,7868 | х | х | х | 77,92 | х | 712553,8 | 159999,3 |
| Среднее значение | 2,904530 | 2,658356 | 7,772303 | 8,505 | 7,112 | х | 505,6 | х | х | 0,15 | 44534,61 | 9999,96 |
| Дисперсия | 0,068322 | 0,044813 | х | х | х | х | х | х | х | х | х | х |
| СКО | 0,2614 | 0,2117 | х | х | х | х | х | х | х | х | х | х |
Получим линейное уравнение: 
Выполнив его потенцирование, получим:
ЗАДАНИЕ
Согласно исходным данным определить параметры уравнения.
Таблица 1 - Исходные данные
| № предприятия | Среднегодовая стоимость ОПФ, млн. руб. | Объем продукции в сопоставимых ценах, млн. руб. | № предприятия | Среднегодовая стоимость ОПФ, млн. руб. | Объем продукции в сопоставимых ценах, млн. руб. | № предприятия | Среднегодовая стоимость ОПФ, млн. руб. | Объем продукции в сопоставимых ценах, млн. руб. |
| 63,5 | 80,8 | 31,6 | 40,7 | 51,1 | 42,1 | |||
| 75,3 | 94,6 | 5,1 | 4,8 | 40,8 | ||||
| 66,1 | 112,1 | 31,6 | 36,2 | 4,3 | ||||
| 33,2 | 34,2 | 56,2 | 79,2 | 31,9 | 36,8 | |||
| 40,4 | 42,4 | 68,1 | 69,1 | 56,8 | 79,2 | |||
| 80,6 | 102,4 | 29,7 | 35,4 | 30,1 | ||||
| 51,5 | 58,6 | 27,3 | 23,3 | 9,8 | ||||
| 49,1 | 53,3 | 47,8 | 45,8 | 10,7 | 11,8 | |||
| 67,2 | 70,7 | 52,1 | 49,9 | 70,5 | 75,2 | |||
| 34,3 | 29,1 | 69,4 | 76,4 | 45,3 | 56,1 | |||
| 33,8 | 33,2 | 73,1 | 118,5 | 81,5 | 79,8 | |||
| 39,6 | 54,3 | 29,4 | 63,7 | 60,3 | ||||
| 50,6 | 45,3 | 49,1 | 66,9 | 65,7 | ||||
| 59,6 | 70,2 | 128,5 | 10,3 | 9,1 | ||||
| 64,2 | 79,8 | 78,1 | 102,3 | 47,2 | 45,8 | |||
| 39,7 | 64,3 | 8,5 | 7,1 | 27,4 | 23,1 | |||
| 56,8 | 46,6 | 29,4 | 32,2 | |||||
| 35,7 | 41,5 | 43,4 | 48,2 | 68,3 | ||||
| 30,1 | 38,1 | 55,2 | 57,7 | 65,1 | 71,3 | |||
| 54,3 | 85,3 | 43,6 | 48,6 | 34,6 | 35,1 | |||
| 20,1 | 18,4 | 91,4 | 109,1 | 31,9 | ||||
| 45,5 | 46,8 | 14,2 | 12,7 | 35,5 | ||||
| 48,7 | 52,6 | 76,1 | 86,7 | 41,1 | 45,6 | |||
| 59,9 | 90,5 | 36,2 | 36,8 | 58,6 | 75,1 | |||
| 72,6 | 86,3 | 44,7 | 67,1 | 69,4 | ||||
| 78,2 | 121,7 | 69,5 | 84,3 | 38,7 | 43,2 | |||
| 41,2 | 53,9 | 46,1 | 69,9 | 41,6 | 59,6 | |||
| 48,1 | 58,3 | 67,1 | 56,5 | 48,4 | ||||
| 55,6 | 57,3 | 117,7 | 179,3 | 45,5 | 58,1 | |||
| 43,7 | 48,2 | 104,2 | 42,2 | |||||
| 91,8 | 109,9 | 109,3 | 155,3 | 61,4 | 84,3 | |||
| 69,3 | 76,7 | 94,3 | 98,9 | 73,5 | ||||
| 73,7 | 112,3 | 89,1 | 92,1 | 20,9 | 21,5 | |||
| 29,1 | 32,4 | 40,7 | 42,1 | 64,3 | 78,9 | |||
| 45,6 | 104,6 | 40,1 | 42,6 | |||||
| 14,7 | 12,1 | 51,3 | 58,9 | 80,9 | 106,9 | |||
| 76,1 | 86,4 | 49,6 | 53,1 | 51,4 | 58,3 | |||
| 36,2 | 36,2 | 63,4 | 80,4 | 49,7 | 53,9 | |||
| 44,8 | 67,7 | 75,2 | 94,1 | 43,2 | 49,2 | |||
| 69,3 | 84,1 | 66,5 | 112,6 | 58,1 | 60,4 | |||
| 46,2 | 69,3 | 33,2 | 72,6 | 104,1 | ||||
| 58,4 | 67,1 | 70,6 | 66,3 | 69,2 | ||||
| 117,2 | 179,2 | 34,5 | 29,4 | 30,1 | 35,9 | |||
| 74,6 | 104,1 | 33,9 | 33,1 | 67,5 | 72,4 | |||
| 155,3 | 39,3 | 54,5 | 69,4 | 100,5 | ||||
| 9,2 | 7,9 | 41,5 | 50,3 | 89,1 | 120,3 | |||
| 115,4 | 163,1 | 59,8 | 70,2 | 35,5 | ||||
| 35,4 | 30,1 | 79,3 | 57,1 | 45,5 | ||||
| 9,1 | 6,2 | 39,3 | 64,5 | 37,7 | 34,9 | |||
| 10,9 | 11,4 | 56,4 | 46,2 | 56,2 | 88,4 | |||
| 70,2 | 75,8 | 35,1 | 41,4 | 45,2 | 35,9 | |||
| 45,3 | 56,1 | 38,9 | 71,8 | 96,3 | ||||
| 81,6 | 76,2 | 54,6 | 85,6 | 26,4 | ||||
| 63,4 | 60,4 | 20,5 | 18,1 | 139,8 | ||||
| 55,2 | 84,3 | 45,1 | 46,9 | 65,5 | 68,1 | |||
| 66,7 | 65,2 | 48,2 | 52,7 | 75,1 | 99,7 | |||
| 10,3 | 9,1 | 59,3 | 90,4 | 71,1 | 96,3 | |||
| 16,2 | 72,4 | 86,1 | 108,2 | |||||
| 39,4 | 42,3 | 16,9 | 56,4 | 89,1 | ||||
| 33,8 | 39,4 | 42,4 | 45,3 | 70,4 | ||||
| 49,2 | 44,1 | 33,1 | 45,9 | 80,9 | ||||
| 30,1 | 20,3 | 49,1 | 44,8 | 30,1 | 25,3 | |||
| 51,4 | 42,1 | 30,5 | 20,1 | 69,9 | 92,6 |
ВОПРОСЫ
3.1 Что такое регрессия.
3.2 Классификация регрессий.
3.3 Сущность метода наименьших квадратов.
3.4 Методы выбора математической функции.
3.5 Сущность графического метода.
3.6 Сущность аналитического метода.
3.7 Сущность экспериментального метода.
3.8 Основные типы кривых, используемые при количественной оценке связей между переменными.
Практическое занятие 24
Корреляционно-регрессионный анализ. оценка качества уравнений
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Оценить тесноту взаимосвязи факторного и результативного признаков можно с помощью коэффициента (индекса) корреляции и детерминации. Используя данные примера ПЗ №8, рассчитаем коэффициент корреляции для линейной функции и индекс корреляции для степенной модели, а также коэффициенты детерминации. В таблице 5 приведена характеристика силы связи в зависимости от значения коэффициента корреляции.
Таблица 5 - Характеристика силы связи между признаками
| Показания тесноты связи - коэффициент корреляции (по модулю) | Характеристика силы связи |
| 0,1 – 0,3 | слабая |
| 0,3 – 0,5 | умеренная |
| 0,5 – 0,7 | заметная |
| 0,7 – 0,9 | высокая |
| 0,9 – 0,99 | весьма высокая |
Для линейной функции:
- коэффициент корреляции: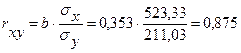 
.
Связь сильная, прямая.
- коэффициент детерминации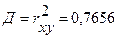 
Следовательно, уравнением регрессии объясняется 76,56 % дисперсии результативного признака, а на долю прочих факторов приходится 23,44% ее дисперсии (т.е. остаточная дисперсия).
Для степенной функции:
- индекс корреляции: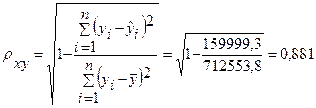 
Связь сильная.
- коэффициент детерминации: Д = 0,7756.
Рассчитать коэффициент эластичности. Коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1 % от своего среднего значения и рассчитывается по формуле:
 .
| (1) |
где 
- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Для уравнения прямой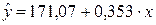 
:
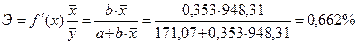
Расчеты показали, что при увеличении доходов населения на 1%, потребительские расходы в среднем вырастут на 0,662 %
Для уравнения степенной зависимости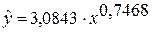 
:
%.
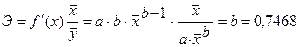Найти величину средней ошибки аппроксимации. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения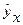 
(табл. 1.2 и 1.3). Найдем величину средней ошибки аппроксимации 
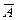по формуле:
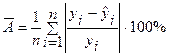
| (2) |
Для линейной: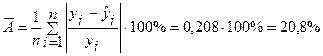 
Для степенной: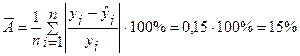 
.
Допустимый предел значений ошибки аппроксимации составляет 8 – 10 %. Обе выбранные модели недостаточно точно описывают исходную информацию. Поэтому данные уравнения регрессии можно использовать только для текущего анализа.
Большое значение ошибки аппроксимации объясняется сильной вариацией исходных данных, так по результативному признаку размах вариации составляет (при минимальном значении 139 и максимальном – 861) 722 тыс. руб. Из этого можно сделать вывод о неоднородности исходной совокупности данных.
Произвести оценку значимости уравнения регрессии. Оценка значимости уравнения регрессии в целом дается с помощью F – критерия Фишера. При этом выдвигается гипотеза, что коэффициент регрессии равен нулю, т.е. b = 0, и, следовательно, фактор х не оказывает влияния на результат у. Для F - теста выполняется сравнение фактического 
и критического (табличного)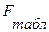 
значений критерия. Фактическое значение определяется из соотношения факторной и остаточной дисперсией, рассчитанных на одну степень свободы:
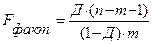
| (3) |
где Д – коэффициент детерминации.
n – число единиц совокупности;
m – число параметров при переменных х.
.
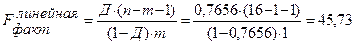
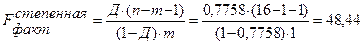Расчетное значение необходимо сравнить с критическим, найденным по специальным таблицам. Табличное значение - это максимально возможное значение критерия под влиянием случайных факторов при степенях свободы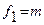 
и 
и уровне значимости a.
Если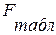 
< 
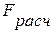, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если 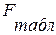> 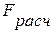, то гипотеза не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Табличное значение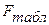 
равно 4,60 пр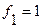и 
и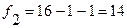 
и a=0,05. Так как, оба расчетных значения превышают табличное значение, это позволяет говорить о статистической значимости обоих уравнений регрессии.
Однако, учитывая, что у степенной функции все рассчитанные характеристики имеют лучшие значения, то для дальнейшего анализа оставляем именно это уравнение .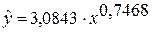
Определить прогнозное значение зависимой переменной 
. Прогнозное значение зависимой переменной определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения независимой переменной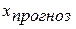 
.
Если прогнозное значение денежных доходов населения составит: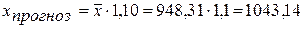 
тыс. руб., тогда прогнозное значение потребительских расходов на душу населения составит:
Ошибка прогноза составит:
 ,
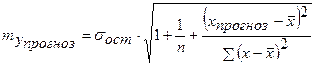| (4) |
где 
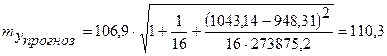тыс. руб.
Предельная ошибка прогноза, которая в 95 % случаев не будет превышена, составит: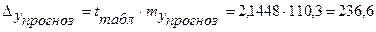 
Доверительный интервал прогноза:
 ± 
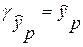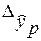
| (5) |
 – ;
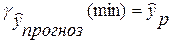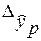| (6) |
 +
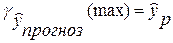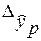
| (7) |
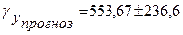
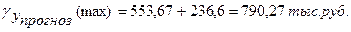
ЗАДАНИЕ
Согласно исходным данным (Практическое занятие 8) произвести оценку тесноты взаимосвязи факторного и результативного признаков.
ВОПРОСЫ
3.1 Что такое регрессия.
3.2 Классификация регрессий.
3.3 Сущность метода наименьших квадратов.
3.4 Методы выбора математической функции.
3.5 Сущность графического метода.
3.6 Сущность аналитического метода.
3.7 Сущность экспериментального метода.
Практическое занятие 25.
Временные ряды в научных исследованиях
Цель и содержание
Цель работы – ознакомиться с основными моделями и методами, прогнозирования приобрести навыки прогнозирования с помощью методов экстраполяции.
В результате выполнения работы студенты должны:
1. Установить цели и задачи исследования;
2. Подготовить исходные данные;
3. Осуществить фильтрацию исходного временного ряда;
4. Осуществить отбор видов аппроксимирующей функции;
5. Оценить параметры математической модели прогнозирования;
6. Выбрать математическую модель прогнозирования;
7. Осуществить точечный и интервальный прогноз;
8. Осуществить верификацию прогноза.
Теоретическое обоснование
Временной ряд – это совокупность значений, какого либо показателя за несколько последовательных моментов или периодов.
Временные ряды бывают моментными (например, списочная численность работников на начало месяца) и интервальными (например, заработная плата в определенные месяцы).
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.
Если во временном ряду проявляется длительная тенденция изменения экономического показателя, то говорят что, имеет место тренд. Таким образом, под трендом понимается изменение, определяющее общее направление развития, основную тенденцию временных рядов.
В связи с этим экономико-математическая динамическая модель, в которой развитие моделируемой экономической системы отражается через тренд ее основных показателей, называется трендовой моделью.
В самом общем случае временной ряд экономических показателей можно разложить на три компоненты:
1. тренд, составляющий которого будем обозначать Тt; 
2. сезонная (циклическая) компонента - St;
3. случайная (стохастическая) компонента - Еt;
Различают следующие виды моделей:
1. Тренд: y(t) = T(t) + E(t)
2. Сезонность (цикличность): y(t) = S(t) + E(t)
3. Тренда и сезонности: y(t) = T(t) + S(t) + E(t)
y(t) = T(t) * S(t) * E(t)
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени или тренд. Этот способ называют аналитическим выравниванием временного ряда.
Для построения трендов чаще всего применяют следующие функции:
1)линейный тренд:
 ;
| (2.1) |
2) гиперболическая:
 ;
| (2.2) |
3) степенная:
 ;
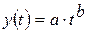| (2.3) |
4) экспоненциальная:
 ;
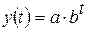| (2.4) |
5) парабола второго и более высоких порядков:
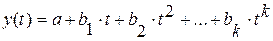
| (2.5) |
Параметры каждого из перечисленных выше трендов можно определить при помощи МНК, используя в качестве независимой переменной время 
, а в качестве зависимой переменной – фактические уровни временного ряда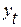 
. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации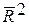 
, рассчитанное для нескольких форм тренда.
Среди большого разнообразия экономико-математических методов, используемых в эконометрике, особое место занимают методы и модели прогнозирования. Для математических методов прогнозирования характерен подбор и обоснование математической модели исследуемого процесса, а также способов определения ее неизвестных параметров. Задача прогнозирования при этом сводится к решению уравнений, описывающих данную модель для заданного момента времени.
Среди математических методов прогнозирования в особую группу выделяются методы экстраполяции, которые отличаются простотой, наглядностью и легко реализуемые на ЭВМ.
Прогнозирование с помощью методов экстраполяции должно включать в себя следующие этапы работ:
1. Установление цели и задачи исследования, анализ объекта прогнозирования.
2. Подготовка исходных данных.
3. Фильтрация исходного временного ряда.
4. Логический отбор видов аппроксимирующей функции.
5. Оценка параметров математической модели прогнозирования.
6. Выбор математической модели прогнозирования.
7. Получение точечного и интервального прогнозов.
8. Верификация прогноза.
Подробнее прогнозирование с помощью методов экстраполяции рассмотрена в п. 5 данной работы.
3 Аппаратура и материалы:
микрокалькулятор, программное обеспечение MS Excel.
