После статистической оценки значимости коэффициентов приступают к проверке математической модели на адекватность.
Указанная процедура производится с помощью критерия Фишера, согласно следующему альтернативному условию:
 , (16)
, (16)
где Fопытн — опытное значение критерия Фишера;
S2{у}н.а. — дисперсия неадекватности, т.е. остаточная дисперсия;
S2{у}воспр — дисперсия воспроизводимости всего эксперимента;
a — уровень значимости;
N — число складываемых дисперсий;
d — число значащих коэффициентов математической модели (b0,
b1,b2 и т.д.).
Величина дисперсии неадекватности вычисляется по формуле:
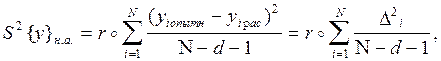 (17)
(17)
где уi расч — расчетное значение функции отклика, получаемое
на основании уравнения регрессии;
уi опытн — среднее значение функции отклика получаемое на опыте;
r — число параллельных опытов;
Fтабл — табличное (критическое) значение Фишера, величина которого вычисляется в зависимости от уровня значимости a и числа степеней свободы большей дисперсии к1 и числа степеней свободы меньшей дисперсии к2. Данное значение выбирается из табл. 4.
Если Fопытн £ Fтабл — гипотеза об адекватности математической модели не отвергается;
Если Fопытн > Fтабл — гипотеза об адекватности математической модели отвергается.
Таблица 4 — Табличные значения критерия Фишера Fтабл, вычисленные в зависимости от значений большей и меньшей дисперсий при уровне значимости a=0,05 (k1 - большая дисперсия и к2 - меньшая дисперсия)
| k2 | Число степеней свободы большей дисперсии k1 | ||||||||
| ¥ | |||||||||
| 19.3 | 19.3 | 19.4 | 19.5 | 19.5 | |||||
| 9.6 | 9.3 | 9.1 | 9.0 | 8.9 | 8.7 | 8.6 | 8.5 | ||
| 7.7 | 6.9 | 6.6 | 6.4 | 6.3 | 6.2 | 5.9 | 5.8 | 5.6 | |
| 6.6 | 5.8 | 5.4 | 5.2 | 5.1 | 5.0 | 4.7 | 4.5 | 4.4 | |
| 6.0 | 5.1 | 4.8 | 4.5 | 4.4 | 4.3 | 4.0 | 3.8 | 3.7 | |
| 5.6 | 4.7 | 4.4 | 4.1 | 4.0 | 3.9 | 3.6 | 3.4 | 3.2 | |
| 5.3 | 4.5 | 4.1 | 3.8 | 3.7 | 3.6 | 3.3 | 3.1 | 2.9 | |
| 5.1 | 4.3 | 3.9 | 3.6 | 3.5 | 3.4 | 3.1 | 2.9 | 2.7 | |
| 5.0 | 4.1 | 3.7 | 3.5 | 3.3 | 3.2 | 2.9 | 2.7 | 2.5 | |
| 4.8 | 4.0 | 3.6 | 3.4 | 3.2 | 3.1 | 2.8 | 2.6 | 2.4 | |
| 4.8 | 3.9 | 3.5 | 3.3 | 3.1 | 3.0 | 2.7 | 2.5 | 2.3 | |
| 4.7 | 3.8 | 3.4 | 3.2 | 3.0 | 2.9 | 2.6 | 2.4 | 2.2 | |
| 4.6 | 3.7 | 3.3 | 3.1 | 3.0 | 2.9 | 2.5 | 2.3 | 2.1 | |
| 4.5 | 3.7 | 3.3 | 3.1 | 2.9 | 2.8 | 2.5 | 2.3 | 2.1 | |
| 4.4 | 3.5 | 3.1 | 2.9 | 2.7 | 2.6 | 2.3 | 2.1 | 1.8 | |
| 4.2 | 3.3 | 2.9 | 2.7 | 2.5 | 2.4 | 2.1 | 1.9 | 1.6 | |
| 4.1 | 3.2 | 2.9 | 2.6 | 2.5 | 2.3 | 2.0 | 1.8 | 1.5 | |
| 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 1.9 | 1.7 | 1.4 | |
| 3.9 | 3.1 | 2.7 | 2.5 | 2.3 | 2.2 | 1.8 | 1.6 | 1.3 | |
| ¥ | 3.8 | 3.0 | 2.6 | 2.4 | 2.2 | 2.1 | 1.8 | 1.5 | 1.0 |
Задание
2.1. Выбрать из задания на практику целевую функцию, которая является обобщенным показателем качества исследуемого процесса или явления.
2.2. Определить основные факторы, оказывающие влияние на целевую функцию, и границы их измерения.
2.3. Указать число опытных точек и количество наблюдений.
2.4. Определить избыточность плана наблюдений.
2.5. Составить матрицу планирования эксперимента.
2.6. Выбрать вид математической модели.
2.7. Вычислить коэффициенты регрессии и определить вид целевой функции.
2.8. Проверить воспроизводимость эксперимента с использованием критерия Кохрена.
2.9. Выполнить статистическую оценку значимости коэффициентов математической модели
2.10. Проверить математическую модель на адекватность, используя критерий Фишера.
2.11. Составить план эксперимента, привести данные, используемые для проверки адекватности математической модели и построить график целевой функции.
2.12. Сформулировать выводы.
ВОПРОСЫ
3.1 Какова последовательность реализации задач исследования?
3.2 Способы определения коэффициентов линейной многофакторной модели.
3.3 Как производится статистическая оценка значимости коэффициентов математической модели?
3.4 Как производится проверка математической модели на адекватность?




