Электроны проводника образуют электронный газ. Хаотические тепловые движения электронов разлагаем на сумму коллективных перемещений электронного газа в виде множества стоячих волн смещений газа от равномерного распределения со всеми возможными длинами волн. На концах проводника электроны не смещаются, так как не могут выйти за пределы проводника, и возникают узлы смещений. В результате смещения газа разлагаются в ряд Фурье из 
стоячих волн, показанных на рисунке. Смещение электронов создает электрическое поле внутри проводника и разность потенциалов на его концах. Найдем флуктуацию этого напряжения, рассматривая каждую волну как гармонический осциллятор с тепловой энергией 
.
Узлы на концах проводника означают, что на длине проводника l укладывается целое число n полуволн
, 
,
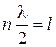где λ – длина волны, тогда
.
C учетом двух проекций спина электрона число волн в интервале частот (0,n) равно
,
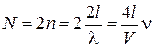где 
; V – скорость волны. В интервале частот d n число волн
.
Каждая волна является гармоническим осциллятором с тепловой энергией kT, тогда энергия dN волн
.
Время распространения волны по проводнику
,
тепловая мощность перемещения электронов
.
Тепловая мощность связана с ЭДС законом Джоуля–Ленца
.
Для фурье-компоненты флуктуационной ЭДС на частоте n находим
. (П.4.2)
Результат получил один из основателей теории информации Гарри Найквист в 1928 г.
Гарри Найквист (1889–1976)
При Т ~ 300 К ЭДС слабо зависит от частоты, в спектре флуктуаций присутствуют все частоты, флуктуации имеют «белый спектр». Из (П.4.2) находим флуктуацию напряжения на концах проводника
, (П.4.3)
где Dn – полоса частот, регистрируемая измерителем сигналов. Теория применима при относительно высокой температуре
,
когда не существенны квантовые эффекты.
Молярная теплоемкость простого тела.
Закон Дюлонга и Пти
Простое вещество состоит из атомов одного химического элемента. Кристаллическая решетка удерживает атом в узле потенциальным полем
.
Гамильтониан узла в виде трехмерного осциллятора
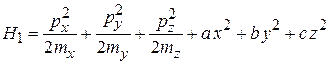
сравниваем с (2.38)
,
находим
, 
.
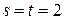Из (2.39)
получаем среднюю тепловую энергию атома
.
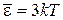Внутренняя энергия моля
.
Молярная теплоемкость
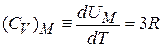. (П.4.4)
Простые твердые тела обладают одинаковой, не зависящей от температуры молярной теплоемкостью – закон Дюлонга и Пти (1819 г.). Закон не применим для объектов, где существенны квантовые явления.
Пьер Луи Дюлонг (1785–1838) Алексиз Терез Пти (1791–1820)
Вопросы коллоквиума
1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.
2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.
3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.
4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц. Наиболее вероятные и средние значения.
5. Распределение Больцмана по координатам для концентрации частиц. Формула Больцмана для однородного поля тяжести.
6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциал. Условие равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.
