Весы – одномерная система с потенциальной энергией
,
x – отклонение указателя от положения равновесия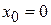 
;
– коэффициент жесткости пружины.
Упругая возвращающая сила
.
При равновесии упругой и гравитационной сил деформация x пропорциональна гравитационной массе тела
.
Добавление массы 
изменяет показание весов на 
,
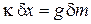тогда флуктуации связаны соотношением
,
где чувствительность
.
Чем меньше коэффициент жесткости, тем выше чувствительность весов.
Получим неустранимую погрешность положения указателя весов
,
используя теорему о распределении тепловой энергии по степеням свободы системы. Сравниваем потенциальную энергию упругой силы
с (2.38)
,
в виде
,
находим
, 
.
С учетом 
из (2.39)
получаем среднюю потенциальную энергию, связанную с одномерным тепловым хаотическим движением весов:
.
Находим 
и получаем флуктуацию положения указателя весов
.
Неустранимой погрешностью измерения массы
вызвана хаотическими тепловыми движениями молекул пружины и окружающего воздуха.
Для уменьшения погрешности необходимо уменьшать температуру и увеличивать чувствительность весов. Это требует уменьшениякоэффициента жесткости, который определяет частоту колебаний указателя весов:
.
Используем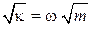 
и находим относительную погрешность измерения
.
При w = 10 Гц, Т = 290 К, m = 10–3 г, получаем d m / m» 10–5.
Предельная чувствительность усилителя сигналов
Колебательного контура
LCR – колебательный контур; У – усилитель
Полезный сигнал, регистрируемый колебательным контуром LRC, поступает на усилитель У и далее на регистратор в виде осциллографа. Усилитель с обратной связью увеличивает амплитуду колебаний напряжения на конденсаторе, начиная с некоторого минимального порогового значения. Оно зависит от коэффициента усиления и определяет минимальную величину полезного сигнала, который можно зарегистрировать устройством. Для устранения зашумленности выходящего сигнала пороговое значение усиливаемого сигнала должно превышать величину тепловых флуктуаций напряжения в контуре. Найдем эту величину.
Хаотическое движение электронов в резисторе R создает кратковременный ток, конденсатор заряжается, в контуре возникают колебания. Из определения электроемкости
получаем связь между среднеквадратичными значениями заряда и напряжения
.
Конденсатор рассматриваем как одномерную систему с энергией
,
где заряд аналогичен импульсу. Сравниваем с гамильтонианом (2.38)
,
находим
, 
.
Из теоремы (2.39)
получаем среднюю тепловую энергию колебательного контура
.
Откуда находим
,
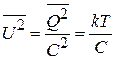
и флуктуацию напряжения
.
Чем выше температура и меньше электроемкость колебательного контура, тем больше флуктуация напряжения на конденсаторе.
Параметры колебательного контура 
выражаем через ширину частотной полосы пропускания сигнала 
и реактивное сопротивление X, используя теорию колебательного контура:
,
.
Мощность, передаваемая от контура к усилителю, достигает максимума при согласованной нагрузке, когда входное сопротивление потребителя, то есть усилителя 
, равняется сопротивлению источника X
.
Получаем
,
тогда
и флуктуация напряжения
. (П.4.1)
Для приемника с полосой пропускания Dn = 10 кГц, входным сопротивлением R у = 10 кОм, температурой Т = 290 К получаем флуктуацию напряжения на входе усилителя d U = 1,6 мкВ, что ограничивает предельную чувствительность приемника.
Приведенный вывод не вскрывает механизма возникновения флуктуаций. Рассмотрим этот процесс.
