Уравнение состояния газа 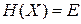 описывает гиперповерхность
описывает гиперповерхность  в фазовом пространстве, на которой находятся микросостояния идеального газа с фиксированными значениями E, V, N. Интегрируем (2.9)
в фазовом пространстве, на которой находятся микросостояния идеального газа с фиксированными значениями E, V, N. Интегрируем (2.9)
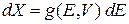 ,
,
и выражаем число микросостояний  внутри гиперповерхности через энергетическую плотность состояний
внутри гиперповерхности через энергетическую плотность состояний
 .
.
Учитываем (2.8) и (2.10)
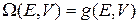 ,
,
 ,
,
находим
 .
.
Переставляем порядок интегрирований и получаем число микросостояний внутри гиперповерхности 
 .
.
Варьируем  по объему при постоянной энергии. От объема зависит гамильтониан, тогда
по объему при постоянной энергии. От объема зависит гамильтониан, тогда
 ,
,
 .
.
Учитываем симметрию величин в аргументе дельта-функции и заменяем
 ,
,
получаем

 .
.
При вычислении внутреннего интеграла учтено
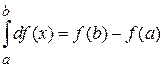 ,
,
на нижнем пределе  , поскольку
, поскольку 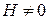 . Используем (2.10а) в виде
. Используем (2.10а) в виде
 ,
,
тогда
 .
.
По определению среднего для распределения 
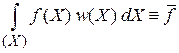
получаем
 . (2.11)
. (2.11)
Внутренняя энергия U
Полная энергия описывается гамильтонианом системы H, и включает кинетическую и потенциальную энергию всех частиц системы. В общем случае эта энергия флуктуирует на микроскопическом уровне. При усреднении по фазовому ансамблю получаем макрохарактеристику – внутреннюю энергию
 .
.
Внутренняя энергия является полной энергией системы, усредненной по фазовому ансамблю.
Давление Р
Давление равно средней силе, действующей со стороны газа на единицу площади стенки сосуда. Давление выражаем через внутреннюю энергию изолированной системы с помощью первого начала термодинамики.
Первое начало термодинамики связывает количества тепла  , переданное газу, с изменением его внутренней энергии
, переданное газу, с изменением его внутренней энергии  и совершенной им работой
и совершенной им работой 
 ,
,
где
 .
.
Для изолированной системы
 ,
,
 ,
,
 .
.
Используем
 . (2.11)
. (2.11)
В результате давление выражается через статистические характеристики микросостояний
 . (2.12)
. (2.12)
Энтропия S
Для равновесного обратимого изотермического процесса изменение энтропии пропорционально количеству полученного тепла
 .
.
Вычисляем
 ,
,
где учтено (2.12) и
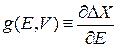 . (2.9а)
. (2.9а)
Используем первое начало термодинамики для равновесного процесса
 ,
,
получаем
 .
.
Сравниваем сомножители бесконечно малой величины между собой
 ,
,
и сомножители конечной величины между собой
 ,
,
где k – постоянная. В результате
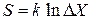 , (2.13)
, (2.13)
 , (2.13а)
, (2.13а)
 . (2.14)
. (2.14)
При рассмотрении конкретных систем и сравнении результатов с формулами термодинамики будет показано, что k – постоянная Больцмана, тогда kT – тепловая энергия.
Из (2.13) получаем – энтропия пропорциональна логарифму числа микросостояний.
Из (2.14) находим – число микросостояний равно произведению энергетической плотности состояний на тепловую энергию. Следовательно, микросостояния создаются за счет тепловой энергии.




