Объект – равновесный идеальный газ из N частиц в объеме V в термостате с температурой Т. Полная энергия системы не постоянная, через стенки сосуда поступают и уходят микроскопические порции энергии. Поэтому разные микросостояния имеют отличающиеся энергии.
Получим распределение микросостояний по фазовому пространству.
Функция распределения
Идеальный газ – любые подсистемы независимые, потенциальная энергия их взаимодействия друг с другом равна нулю. Систему делим на подсистемы 1 и 2. Соответствующие гамильтонианы связаны соотношением
.
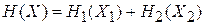Распределения для подсистем и для всей системы выражаются по теореме Лиувилля через гамильтонианы
,
,
.
По теореме об умножении вероятностей независимых событий распределения связаны
,
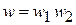тогда
.
Логарифмируем
,
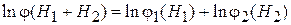берем бесконечно малое приращение – дифференциал
,
где 
.
Учитываем, что 
и 
– независимые величины, тогда
.
Равенство выполняется при условии
,
где k – постоянная Больцмана. Далее будет показано, что T – температура.
Следовательно:
– универсальная функция, удовлетворяющая уравнению:
.
Интегрируем
.
Полагаем
,
как показано далее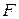 
– свободная энергия системы. Получаем каноническое распределение
(2.15)
– вероятность обнаружения микросостояний в единице объема фазового пространства около точки X,
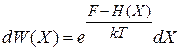(2.15а)
– вероятность обнаружения микросостояний в объеме dX фазового пространства около точкиX.
Статистический интеграл системы Z
Полагаем 
, тогда
,
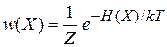. (2.16)
Условие нормировки вероятности
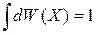
дает макрохарактеристику – статистический интеграл системы
. (2.17)
Статистический интеграл частицы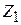 
Для идеального газа из N тождественных частиц
,
,
где 
– гамильтониан частицы n.
С учетом 
интеграл (2.17)
распадается на произведение N одинаковых интегралов. Получаем выражение стат. интеграла системы Z через стат. интеграл частицы Z 1
, (2.18)
где статистический интеграл частицы
, (2.19)
.
Для независимых видов движения частицы: поступательного, вращательного, колебательного и внутреннего
,
тогда
. (2.20)
Для N частиц
. (2.21)
Далее получено
. (2.22)
Для двухатомной молекулы с моментом инерции J и частотой собственных колебаний w
,
. (2.23)
Физический смысл T
Общее начало термодинамики утверждает –если температуры систем одинаковые, то приведение систем в тепловой контакт не изменяет их макросостояний.
До контакта систем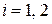 
их функции распределения
. (2.16)
В момент контакта в силу независимости систем их общее распределение по теореме об умножении вероятностей
.
С течением времени гамильтонианы изменяются, их сумма сохраняется. Если температуры систем были одинаковыми, то распределение не должно меняться согласно общему началу термодинамики. Это возникает при 
. Следовательно, Т – температура по шкале Кельвина.
