Состояния с энергией Е находятся в фазовом пространстве на гиперповерхности 
. Изменение энергии на dE вызывает переход к соседней гиперповерхности, объем внутри гиперповерхности меняется на dX, причем
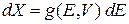, (2.9а)
где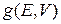 
– энергетическая плотность состояний.
В каноническом распределении (2.15) и (2.16)
,
переходим от гамильтониана 
к переменной энергии системы Е. С учетом (2.9а) получаем
(2.24)
– вероятность обнаружения микросостояний с энергией в интервале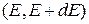 
.
Свободная энергия и статистический интеграл
Из (2.24) получаем соотношение между свободной энергией F и статистическим интегралом Z
,
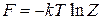. (2.25)
Полученное соотношение выражает термодинамическую характеристику F через величину Z, которая вычисляется по гамильтониану системы
.
Внутренняя энергияUи статистический интеграл
Внутренняя энергия является средним значением полной энергии системы
.
Используем (2.16) и (2.17)
 ,
,
|
находим
,
где воспользовались
, 
.
Учитываем
,
получаем выражение внутренней энергии через статистический интеграл
. (2.26)
Уравнение Гиббса–Гельмгольца
Соотношение между внутренней энергией и свободной энергией называется в термодинамике уравнением Гиббса–Гельмгольца. Для его получения исключим статистический интеграл из (2.25) и (2.26).
Выражение (2.25)
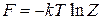
записываем в виде
и подставляем в (2.26). Получаем известное в термодинамике уравнение Гиббса–Гельмгольца
. (2.27)
Следовательно, в (2.25) F – свободная энергия.
Из первого равенства в (2.27) выражаем
.
Интегрируем
. (2.28)
Свободная энергия выражена через внутреннюю энергию.
Термодинамический потенциал
Потенциалом называется функция состояния системы, не зависящая от пути перехода системы в это состояние. Тогда изменение потенциала при переходе системы из начального состояния в это же состояние по замкнутому пути равно нулю и потенциал является полным дифференциалом своих аргументов
.
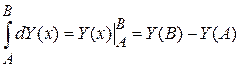Примером потенциальной функции является электростатический потенциал 
, являющийся функцией координат.
Термодинамические потенциалы являются функциями макроскопических характеристик системы: T, V, P, S, N, и отличаются друг от друга набором этих характеристик.
Внутренняя энергия является термодинамическим потенциалом
,
полный дифференциал
.
Свободная энергия является термодинамическим потенциалом
,
. (2.30а)
Смысл свободной энергии
Используем соотношение термодинамики
. (2.31)
Берем дифференциал
. (2.31а)
Для равновесного, обратимого процесса используем определение энтропии и первое начало термодинамики
,
,
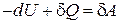тогда
,
и из (2.31а) при 
получаем
.
Свободная энергия является частью внутренней энергии, которая при изотермическом процессе переходит в работу.
Из (2.31) следует, что при 
свободная энергия равна внутренней энергии.
Связанная энергия
– часть внутренней энергии, которая при изотермическом процессе не может быть превращена в работу и выделяется в виде теплоты.
Понятия свободной и связанной энергий ввел Герман Гельмгольц в 1847 г.
