4. Зв’язності. ("а)("в) (а¹в Þ а<в або в<а), а, в ÎR.
5. Правило скорочення для додавання: ("а) ("в) ("с) (а+с<в+с Þа<в), а, в, с ÎR.
6. Монотонність множення:
а) ("а) ("в) ("с) (а < в Ù с > 0 Þ ас < вс), а, в, с ÎR.
б) ("а) ("в) ("с) (а < в Ù с < 0 Þ ас > вс), а, в, с ÎR.
7. Правило скорочення множення:
("а) ("в) ("с) (ас < вс Ù с > 0 Þ а < в), а, в, с ÎR.
("а) ("в) ("с) (ас < вс Ù с < 0 Þ а > в), а, в, с ÎR.
8. Рівняння з однією змінною
Візьмемо два вирази із змінною: 4х і 5х+2. З’єднавши їх знаком рівності, одержимо речення 4х=5х+2. Воно містить змінну і при підстановці значень змінної перетворюється уявлення. Наприклад, при х=1 речення 4х=5х+2 перетворюється в хибну числову рівність 4·1=5·1+2, а при х=-2 – в істинну 4·(-2)=5·(-2)+2. Тому речення 4х=5х+2 є висловлювальна форма. Її називають рівністю із змінною або рівнянням з однією змінною.
В загальному вигляді поняття рівняння з однією змінною можна визначити так:
Означення. Нехай f(х) і g(х) – два вирази із змінною х і областю визначення Х. Тоді висловлювальна форма виду f(х) = g(х) називається рівнянням із однією змінною.
Значення змінної х із множини Х, при якому рівняння перетворюється в істинну числову рівність, називається його розв’язком (або коренем). Знайти множину рішень даного рівняння – значить розв’язати це рівняння.
Наведемо декілька прикладів рівнянь із однією змінною.
1) 4х=5х+2, х  R. Ця рівність перетворюється в істинну числову рівність тільки при х=-2. Значить, його множина розв’язків є
R. Ця рівність перетворюється в істинну числову рівність тільки при х=-2. Значить, його множина розв’язків є  .
.
2) (х-1) (х+2)=0, х  R. Ця рівність з однією змінною перетворюється в істинну числову рівність при х=1 і при х=-2. Тобто, множина розв’язків даного рівняння така:
R. Ця рівність з однією змінною перетворюється в істинну числову рівність при х=1 і при х=-2. Тобто, множина розв’язків даного рівняння така:  .
.
3) (3х+1)·2=6х+2, х  R. Якщо розкрити дужки у виразі, який стоїть в лівій частині, то дане рівняння набуває вигляду 6х+2=6х+2. Отриманий запис означає, що таке рівняння перетворюється в істинне висловлення при будь-якому значенні змінної х. В цьому випадку говорять, що множина розв’язків даного рівняння є множиною дійсних чисел.
R. Якщо розкрити дужки у виразі, який стоїть в лівій частині, то дане рівняння набуває вигляду 6х+2=6х+2. Отриманий запис означає, що таке рівняння перетворюється в істинне висловлення при будь-якому значенні змінної х. В цьому випадку говорять, що множина розв’язків даного рівняння є множиною дійсних чисел.
4) (3х+1)·2=6х+1, х  R. Легко впевнитися в тому, що дане рівняння не перетворюється в істинну числову рівність ні при одному дійсному значенні х: після перетворень в лівій частині маємо 6х+2, а в правій 6х+1, але 1
R. Легко впевнитися в тому, що дане рівняння не перетворюється в істинну числову рівність ні при одному дійсному значенні х: після перетворень в лівій частині маємо 6х+2, а в правій 6х+1, але 1  2. В цьому випадку говорять, що дані рівняння не мають розв’язку або що множина його розв’язків порожня.
2. В цьому випадку говорять, що дані рівняння не мають розв’язку або що множина його розв’язків порожня.
У початковому курсі математики розглядаються найпростіші рівняння виду х+а=b, а-х= b, х-а= b, х·а= b, х:а= b і інші, де а, b – цілі невід’ємні числа, х – змінна. Поняття рівняння і його розв’язків визначаються неявно, через контекст і в ході розв’язування таких рівнянь у дітей повинно бути поступово сформоване поняття рівняння як рівності, яка містить невідоме число, позначене буквою. Вони повинні зрозуміти, що кожен раз, як ми зустрічаємося з рівнянням, задача заключається в тому, щоб знайти те значення невідомого числа, при якому рівність буде правильною.
Рівносильність рівнянь. Щоб розв’язати дане рівняння, його, як правило, перетворюють, замінюючи послідовно іншими, найбільш простішими. Цей процес заміни продовжують до тих пір, доки не отримають рівняння розв'язок якого можна знайти відомим способом. Але щоб ці розв'язки були розв'язками даного рівняння, необхідно, щоб в процесі перетворень отримались рівняння, множини коренів яких співпадають. Такі рівняння називають рівносильними.
Означення. Два рівняння називаються рівносильними, якщо їх множини розв’язків рівні.
Наприклад, рівняння (х+1)2=9 і (х-2)·(х+4)=0 рівносильні на множині дійсних чисел, так як множина розв’язків першого рівняння 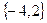 і множина розв’язків другого рівняння
і множина розв’язків другого рівняння  рівні.
рівні.
Визначимо тепер, які перетворення дозволяють одержати рівняння, рівносильні даному. Ці перетворення знайшли відображення в наступних теоремах.
Теорема 1. Нехай рівняння f(х) = g(х) задано на множині Х і h(x) – вираз, визначений на тій же множині. Тоді рівняння f(х) = g(х) (1) і f(x)+ h(x)= g(х)+ h(x) (2) рівносильні на множині Х.
Цю теорему можна сформулювати інакше: якщо до обох частин рівняння з областю визначення Х додати один і той же вираз із змінною, визначене на тій же множині Х, одержимо нове рівняння, рівносильне даному.
Доведення. Позначимо через Т1 множину розв’язків рівняння (1), а через Т2 множину розв’язків рівняння (2). Тоді рівняння (1) і (2) будуть рівносильними, якщо Т1=Т2. Але щоб переконатися в цьому необхідно показати, що кожен корінь із Т1 є коренем рівняння (2) і, навпаки, кожен корінь із Т2 є коренем рівняння (1).
Нехай число а – корінь рівняння (1). Тоді а  Т1 і при підстановці в рівняння (1) перетворює його в істинну числову рівністьf(а) = g(а), а вираз h(x) перетворює в числовий вираз h(а). Додамо до обох частин істинної рівності f(а) = g(а) числовий вираз h(а). Одержимо, істинну числову рівність f(a)+h(a)=g(a)+h(a).
Т1 і при підстановці в рівняння (1) перетворює його в істинну числову рівністьf(а) = g(а), а вираз h(x) перетворює в числовий вираз h(а). Додамо до обох частин істинної рівності f(а) = g(а) числовий вираз h(а). Одержимо, істинну числову рівність f(a)+h(a)=g(a)+h(a).
Але ця рівність говорить про те, що число а є також і коренем рівняння (2).
Отже, доведено, що кожен корінь рівняння (1) є коренем і рівняння (2), тобто Т1  Т2.
Т2.
Нехай тепер b – корінь рівняння (2). Тоді b  Т2 і при підстановці в рівняння перетворює його в істинну числову рівність f(b)+h(b)=g(b)+h(b).
Т2 і при підстановці в рівняння перетворює його в істинну числову рівність f(b)+h(b)=g(b)+h(b).
Додамо до обох частин цього рівняння числовий вираз - h(b). Одержимо істинну числову рівність f(b)= g(b), яке говорить про те, що число b – корінь рівняння (1).
Тобто, доведено, що кожен корінь рівняння (2) є і коренем рівняння (1), тобто Т2  Т1.
Т1.
Так як Т1  Т2 і Т2
Т2 і Т2  Т1, то по визначенню рівних множин Т1=Т2, а значить, рівняння (1) і (2) рівносильні на множині Х.
Т1, то по визначенню рівних множин Т1=Т2, а значить, рівняння (1) і (2) рівносильні на множині Х.
При розв’язуванні рівнянь частіше використовується не сама дана теорема, а наслідки із неї:
1. Якщо до обох частин рівняння додати одне і теж число, то одержимо рівняння, рівносильне даному.
2. Якщо який-небудь доданок (числовий вираз або вираз із змінною) перенести з однієї частини рівняння в іншу, змінивши знак додання на протилежний, то одержимо рівняння, рівносильне даному.
Теорема 2. Нехай рівняння f(x) = g(x) задано на множині Х і h(x) – вираз, визначений на тій же множині і не дорівнює нулю ні при яких значеннях х із множини Х. Тоді рівняння f(x) = g(x) і f(x)∙h(x)=g(x)∙h(x) рівносильні на множині Х.
Доведення цієї теореми аналогічне доведенню теореми 1.
З теореми 2 випливає наслідок, який часто використовується при розв’язуванні рівнянь:
Якщо обидві частини рівняння помножити (або розділити) на одне і теж число, відмінне від нуля, то одержимо рівняння, рівносильне даному.
Розв’яжемо рівняння  , і вияснимо, які теоретичні положення при цьому були використані.
, і вияснимо, які теоретичні положення при цьому були використані.
| Хід розв’язання | Використані теоретичні положення |
1. Зведемо вираз, який знаходиться в лівій і правій частинах рівняння до спільного знаменника:  
| Виконали тотожне перетворення виразу в лівій частині рівняння, одержали рівняння, рівносильне даному. |
| 2. Відкинемо спільний знаменник: 6-2х=х. | Помножили на 6 обидві частини рівняння (теорема 2), одержали рівняння, рівносильне попередньому і, значить, даному. |
| 3. Вираз – 2х переносимо в праву частину рівняння: 6=х+2х. | Скориставшись наслідком із теореми 1 (або згідно теореми 1 додали до обох частин вираз 2х, визначений для всіх дійсних чисел), одержали рівняння, рівносильне попередньому і, значить, даному. |
| 4. Звели подібні члени в правій частині рівняння: 6=3х. | Виконали тотожне перетворення, одержали рівняння, рівносильне попередньому і, значить, даному. |
| 5. Розділили обидві частини рівняння на 3: х=2. | Скористались наслідком із теореми 2 (або згідно теоремі 2 помножили обидві частини рівняння на  ), одержали рівняння, рівносильне попередньому і, значить, даному. ), одержали рівняння, рівносильне попередньому і, значить, даному.
|
Таким чином, множина розв’язків даного рівняння складається з одного числа 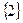 .
.
Візьмемо тепер рівняння х(х-1)=2х, х  R. Іноді учні розв’язують його так: ділять обидві частини на х, одержують рівняння х-1=2, звідки знаходять, що х=3, і роблять висновок:
R. Іноді учні розв’язують його так: ділять обидві частини на х, одержують рівняння х-1=2, звідки знаходять, що х=3, і роблять висновок: 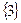 - множина розв’язків даного рівняння.
- множина розв’язків даного рівняння.
Але чи вірно розв’язане дане рівняння? Чи знайдені всі такі дійсні значення х, які перетворюють рівняння х (х-1)=2х в істинну числову рівність?
Не важко бачити, що при х=0 дане рівняння перетворюється в істинну числову рівність 0∙(0-1)=2∙0. Значить, 0 – корінь даного рівняння. Чому ж виникла втрата цього кореня?
Справа в тому, що рівняння х-1=2 не рівносильне рівнянню 2(х-1)=2х на множині дійсних чисел, так як отримано з останнього множенням на вираз  , який визначений не для всіх дійсних чисел (зокрема, при х=0 воно не має змісту), тобто нами не виконано умову теореми 2, що і привело до втрати кореня.
, який визначений не для всіх дійсних чисел (зокрема, при х=0 воно не має змісту), тобто нами не виконано умову теореми 2, що і привело до втрати кореня.
Як правильно розв’язати рівняння х(х-1)=2х? Розглянемо один із можливих варіантів рішення.
| Хід розв’язання | Використані теоретичні положення |
| 1. Перенесемо вираз 2х з правої частини в ліву: х(х-1)-2х=0. | Скористалися слідуванням з теореми 1, одержали рівняння, рівносильне даному. |
| 2. Винесемо в лівій частині рівняння за дужки х і наведемо подібні члени: х(х-3)=0. | Виконали тотожне перетворення, вони не порушили рівносильності рівняння. |
| 3. Творення двох множників рівно нулю в тому і тільки в тому випадку, коли хоча б один із них рівний нулю, тому х=0 або х-3=0. | Скористалися умовою рівності нулю творення декількох множників, одержали сукупність рівнянь, рівносильних висхідному. |
| 4. Переносячи число 3 в праву частину другого рівняння, одержимо: х=0 або х=3. | Скориставшись слідуванням з теореми 1, одержали рівняння, рівносильне рівнянню х-3=0. |
Таким чином, множина розв’язків даного рівняння складається із двох чисел 0 і 3, є вигляд  .
.
Зазначимо, що невиконання умов теорем 1 і 2 може привести не тільки до втрати коренів рівнянь, але і до появи так званих сторонніх коренів.
Які корені називаються сторонніми?
Нехай дані два рівняння: f1(x)=g1(x) (1) і f2(x)=g2(x) (2). Якщо відомо, що всі корені рівняння (1) є коренями рівняння (2), то про рівнянні (2) можна сказати, що воно слідує з рівняння (1). Якщо ж рівняння (2) має корені, які не задовольняють рівняння (1), то вони і будуть сторонніми для рівняння (1). Наприклад, розв’язуючи рівняння 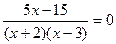 , ми звільнюємося від знаменника, помноживши обидві частини рівняння на (х=2) (х-3), і отримуємо 5х-15=0, звідки х=3. Але при х=3 знаменник дробу
, ми звільнюємося від знаменника, помноживши обидві частини рівняння на (х=2) (х-3), і отримуємо 5х-15=0, звідки х=3. Але при х=3 знаменник дробу  , перетворюється в нуль, і тому х=3 не може бути коренем даного рівняння, тобто х=3 є для нього стороннім коренем.
, перетворюється в нуль, і тому х=3 не може бути коренем даного рівняння, тобто х=3 є для нього стороннім коренем.
Взагалі, якщо при розв’язуванні рівняння його замінюють наслідком (а не рівносильним рівнянням), то треба знайти всі корені рівняння-наслідку, а потім їх перевірити, підставивши в дане рівняння. Сторонні корені відкидають.
Потрібно зауважити, що поява сторонніх коренів менш «небезпечне» явище, чим їх втрата. Тому при розв’язуванні рівнянь необхідно в першу чергу строго слідкувати за правильним використанням теорем про рівносильність.
В початковому курсі математики теоретичною основою розв’язування рівнянь є взаємозв’язок між компонентами і результатами дій. Наприклад, розв’язування рівняння (х∙9):24=3 обґрунтовується слідуючим чином. Так як невідоме знаходиться в діленому, то, щоб знайти ділене, треба дільник помножити на частку: х∙9=24∙3, або х∙9=72. Щоб знайти невідомий множник, треба добуток поділити на відомий множник: х=72:9, або х=8. Отже, рішенням даного рівняння є число 8.
9. Нерівність з однією змінною. Рівносильність нерівностей
Речення виду 2х+7 >10-х, х2+7х<2, (х+2) (2х-3)>0 називають нерівностями з однією змінною.
Означення. Нехай f(x) і g(x) – два вирази із змінною х і областю визначення Х. Тоді нерівність виду f(x)>g(x) або f(x)<g(x) називається нерівністю з однією змінною.
Значення змінної х із множини Х, при якому нерівність обертається в істинну числову нерівність називається його розв’язком. Знайти множину розв’язків даної нерівності – значить розв’язати цю нерівність.
В шкільному курсі математики розглядаються різноманітні нерівності з однією змінною. Нас будуть цікавити в основному нерівності першого степеня. В основі розв’язування таких нерівностей так як і розв’язування рівнянь, лежить поняття рівносильності і теореми про рівносильність нерівностей.
Означення. Дві нерівності називаються рівносильними, якщо їх множини розв’язків рівні.
Наприклад, нерівності 2х+7>10 і 2х>3 рівносильні, так як їх більшість рішень рівні і являють собою проміжок 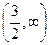 .
.
Теореми про рівносильність нерівностей і наслідки з них по своєму змісту схожі на відповідні теореми про рівносильність рівнянь, а доведення їх проводяться аналогічно доведенням теореми 1 про рівносильності рівнянь.
Теорема 3. Нехай нерівність f(x)>g(x) задано на множині Х і h(x) – вираз, визначений на тій же множині. Тоді нерівності х(х)>g(x) і f(x)+h(x)>g(x)+h(x) рівносильні на множині Х.
З цієї теореми випливають наслідки, які часто використовуються при розв’язуванні нерівностей:
1. Якщо до обох частин нерівності f(x)>g(x) додати одне і теж дійсне число d, то одержимо нерівність f(x)+d>g(x)+d, рівносильну даній.
2. Якщо який-небудь доданок (числовий вираз або вираз із змінною) перенести з однієї частини нерівності в іншу, змінивши знак доданка на протилежний, то одержимо нерівність, рівносильну даній.
Теорема 4. Нехай нерівність f(x)>g(x) задано на множині Х і h(x) – вираз, визначений на тій же можині і для всіх х з множини Х h(x)>0. Тоді нерівності f(x)>g(x) і f(x)∙h(x)>g(x)∙h(x) рівносильні на множині Х.
З цієї теореми випливає наслідок:
Якщо обидві частини нерівності f(x)>g(x) помножити на одне і теж від’ємне дійсне число d, то отримаємо нерівність f(x)∙d<g(x)∙d, рівносильну висхідній.
Теорема 5. Нехай нерівність f(x)>g(x) задано на можині Х і h(x) – вираз, визначений на тій же множині і для всіх х з множини Х h(x)<0. Тоді нерівності f(x)>g(x) і f(x)∙h(x)<g(x)∙h(x) рівносильні на множині Х.
З цієї теореми виходить наступне:
Якщо обидві частини нерівності f(x)<g(x) помножити на одне і те ж від’ємне дійсне число d і знак нерівності змінити на протилежний, то одержимо нерівність f(x)∙d<g(x)∙d, рівносильну даній.
Розв’яжемо нерівність 5х-5<2х-16, х  R, і вияснимо, які теоретичні положення були при цьому використані.
R, і вияснимо, які теоретичні положення були при цьому використані.
| Хід розв’язання | Використані теоретичні положення |
| 1. Перенесемо вираз 2х в ліву частину, а число – 5 в праву: 5х-2х<16+5. | Скористувались наслідком 2 із теореми 3, одержали нерівність, рівносильну даній. |
| 2. Зведемо подібні члени в лівій і правій частинах нерівності: 3х<21. | Виконали тотожне перетворення виразів в лівій і правій частинах нерівності, вона не порушили рівносильності нерівностей. |
| 3. Розділимо обидві частини нерівності на 3: х<7. | Скористувались наслідком з теореми 4, одержали нерівність, рівносильну даній. |
Розв’язком нерівності х<7 є проміжок  . Таким чином множина розв’язків нерівності 5х-5<2х+16 є множина чисел
. Таким чином множина розв’язків нерівності 5х-5<2х+16 є множина чисел  .
.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Боровик В. Н. Курс математики: Навч. посібник / - К.: Вища пік., 1995.- С. 238-240, 244-247, 248-259.
2. Кухар В. М. Математика (практикум): Навч. посібник / - К.: Вища пік., 1989.- С. 79-85.
3. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. -К.: Вища пік., 1987. - С. 76-77.
4. Стойлова Л. П. Основи начального курса математики. М.: Просвещение. 1988. - С. 242-247. 252-259.
 Практичне заняття № 5
Практичне заняття № 5
Тема. Вирази. Рівняння та нерівності, способи їх розв’язування
Мета. Застосувати теоретичні відомості про рівняння та нерівності до розв’язування вправ.
Студенти повинні знати:
· числові вирази;
· вирази із змінними;
· тотожні перетворення виразів. Тотожності;
· числові рівності і нерівності;
· основні властивості числових рівностей;
· основні властивості числових нерівностей;
· рівняння з однією змінною. Множина коренів рівняння. Рівносильні рівняння;
· нерівності з однією змінною.
Студенти повинні вміти:
· використовувати теореми про рівносильність рівнянь;
· розв'язувати нерівності з однією змінною, використовуючи теореми про
рівносильність нерівностей;
· розв'язувати текстові задачі з допомогою складання рівнянь.
Література
1. Курс математики: Навч. посібник / В. Н. Боровик. – К.: Вища шк., 1995. С. 238 – 287. 349 – 379.
2. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1980. С. 153-154, 157-161.
3. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1987. С. 192 -199.
4. Основы начального курса математики: Учеб. пособие Л. П. Стойлова. - М. “Просвещение” 1988. С. 242 - 307.
План та хід заняття
І. Актуалізація опорних знань числові вирази;
1. Вирази із змінними.
2. Тотожні перетворення виразів. Тотожності.
3. Числові рівності і нерівності.
4. Основні властивості числових рівностей.
5. Основні властивості числових нерівностей.
6. Рівняння з однією змінною. Множина коренів рівняння. Рівносильні рівняння. Теорема про рівносильність рівнянь.
7. Нерівності з однією змінною.
ІІ. Розв’язування вправ
1. Перевірте, чи є число -4 коренем рівняння х-0,5∙(х-12)=13-0,25∙х, якщо воно задано на множині дійсних чисел.
2. Рівняння 2х4 +4х2-6=0 розглядається на множині натуральних чисел. Поясніть, чому х=1 є коренем рівняння, а х=2 і х=-1 не є коренями цього рівняння.
3. Замість трьох крапок поставте або «необхідно», або «достатньо», або «необхідно і достатньо» так, щоб отримати істинні висловлювання:
1) Для того, щоб число а було коренем рівняння  , …, щоб число а належало області визначення рівняння.
, …, щоб число а належало області визначення рівняння.
2) Для того, щоб число а було коренем рівняння  , …, щоб при підстановці числа а замість х рівняння перетворювалось в правильну числову рівність.
, …, щоб при підстановці числа а замість х рівняння перетворювалось в правильну числову рівність.
3) Для того, щоб число а було коренем рівняння  , …, щоб число а належало області визначення і при підстановці числа а замість х рівняння перетворювалось в правильну числову рівність.
, …, щоб число а належало області визначення і при підстановці числа а замість х рівняння перетворювалось в правильну числову рівність.
4. Чи правильні висловлення:
1) Для того, щоб добуток (х-3)(х+5)(х-1) дорівнював нулю, необхідно, щоб х=3.
2) Для того, щоб добуток (х-3)(х+5)(х-1) був рівним нулю, достатньо, щоб х=1.
5. Учень розв’язав рівняння 5х+15=3х+9 так:
5(х+3)=3(х+3); 5=3 – і сказав, що це рівняння коренів не має, так як його розв’язання приводить до хибної рівності. Чи правий учень?
6. Розв’яжіть рівняння  і визначте, яке його перетворення призводить до появи стороннього кореня х=2.
і визначте, яке його перетворення призводить до появи стороннього кореня х=2.
7. Встановіть, які з наступних пар рівнянь рівносильні на множині дійсних чисел:
1) 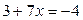 і
і 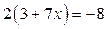 ;
;
2) 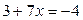 і
і 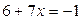 ;
;
3) 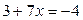 і
і  .
.
8. Розв’яжіть рівняння (всі вони визначені на множині дійсних чисел) і поясніть, які теоретичні положення були при цьому використані:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 
9. Розв’яжіть рівняння, використовуючи залежність між компонентами і результатами дій:
1) (х+70)·4=328;
2) 560:(х+9)=56;
3) (85·х+765):170=98;
4) (х-13581):709=36.
10. Розв’яжіть рівняння різними способами:
1) (х+1)2+3(х-1)=0;
2) (х+1)(х-2)+(х-2)(х+4)=6(2х+5).
11. При яких значення х вирази 2 х +3(х +2) і  мають рівні значення?
мають рівні значення?
12. Розв'яжіть задачі алгебраїчним способом:
1) На першій поличці на 16 книжок більше, ніж на другій. Якщо з кожної полиці зняти по 3 книжки, то на першій полиці книжок буде в півтора рази більше, ніж на другій. Скільки книжок на кожній полиці?
2) 16 км від турбази до санаторію велосипедист проїхав за 1 год 10 хв. Перші 40 хвилин цього часу він їхав з однією швидкістю, а решту часу – зі швидкістю, на 3 км/год меншою. Знайдіть швидкість велосипедиста на першій ділянці шляху.
13. Чи є число 3 розв’язком нерівності  <
<  , визначеної на множині дійсних чисел? А число 4,25?
, визначеної на множині дійсних чисел? А число 4,25?
14. Чи рівносильні на множині дійсних чисел наступні пари нерівностей:
1)  <
<  і
і 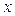 >3;
>3;
2)  >0 і
>0 і  >0;
>0;
3) 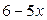 >
>  і
і 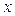 <2?
<2?
15. Які з наступних висловлень істинні:
1)  <
<  >4; 3)
>4; 3) 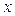 <
<  <5;
<5;
2) 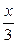 <
< 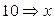 <30; 4)
<30; 4) 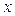 <
<  <20?
<20?
16. Розв'яжіть нерівності і поясніть, які теоретичні положення були при цьому використані:
1)  <
< 
2) 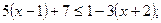 4)
4) 
3) 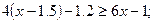 5)
5) 
17. Доведіть, що розв’язком нерівності  >
>  є будь-яке дійсне число.
є будь-яке дійсне число.
18. Доведіть, що не існує дійсного числа, яке є розв’язком нерівності  >
>  .
.
19. Доведіть, що при будь-якому дійсному а значення виразу  менше, ніж значення виразу
менше, ніж значення виразу 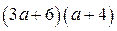 .
.
20. Одна сторона трикутника дорівнює 18 см, а друга 23 см. Встановіть:
1) якою може бути найменша довжина третьої сторони (у см);
2) якою може бути найбільша довжина третьої сторони (у см).
21. Одна сторона трикутника дорівнює 5 м, а друга 8 м. Які натуральні значення може приймати довжина третьої сторони, якщо периметр трикутника:






