В недесяткових системах числення 3 страница

 

5. Ознаки подільності чисел на 2 і на 5

Ознаки подільності на 2, 3, 4, 5, 9 чисел, записаних у десятковій системі числення, відомі з математики середньої школи. Обґрунтуємо ці ознаки, спираючись на введене означення відношення подільності та його властивості.

Теорема (ознака подільності на 2 і 5). Для того щоб число ділилося на 2 (на 5), необхідно й достатньо, щоб на 2 (на 5) ділилося число його одиниць.

Доведення. Запишемо число а = а_nа_n-1...а₀ у вигляді суми розрядних одиниць, яку розіб'ємо на два доданки: а=(а_n10ⁿ+…a₁10) + а_n. Як бачимо, перший доданок ділиться і на 2, і на 5. Отже, щоб сума ділилася на 2 або на 5, необхідно й достатньо, щоб і другий доданок а_n ділився відповідно на 2 або на 5. Теорему доведено.

Наслідок 1. Для того щоб число а ділилося на 2, необхідно й достатньо, щоб воно закінчувалося однією з цифр 0, 2, 4, 6, 8.

Наслідок 2. Для того щоб число а ділилося на 5, необхідно й достатньо, щоб воно закінчувалося цифрою 0 або 5.

 

6. Ознаки подільності чисел на 4 і на 25

Теорема (ознака подільності на 4 і 25). Для того щоб число ділилося на 4 (на 25), необхідно й достатньо, щоб на 4 (на 25) ділилося число, утворене його двома останніми цифрами.

Доведення. Число а = а_nа_n-1...а₀ запишемо у вигляді суми двох доданків: a = (а_n10ⁿ +... +a₂10²) + (a₁10 + a₀). Перший до­данок ділиться як на 4, так і на 25. Отже, число а як сума двох до­данків ділиться на 4 (на 25) тоді і тільки тоді, коли на 4 (на 25) ділиться число a₁a₀ = a₁10+a₀, утворене двома останніми цифрами числа а. Теорему доведено.

 

7. Ознаки подільності чисел на 3 і на 9

Теорема (ознака подільності на 3 і на 9). Для того щоб чис­ло а ділилося на 3 або на 9, необхідно і достатньо, щоб на 3 або на 9 ділилася сума цифр цього числа.

Доведення. Запишемо число а у вигляді: а =a_n10ⁿ +...+a₁10+a₀. Оскільки 10=9+1, 10² = 99+1,..., 10ⁿ = 99...9 + 1, то а_n (99...9 + 1) +... + a₁ (9+1) + а₀ =. (а_n99.2..9+…+a₁9)+(a_n+…+a₁+a₀).

n

Перші доданки суми діляться як на 3, так і на 9. Отже, для того щоб число а ділилося на 3 або на 9, необхідно й достатньо, щоб сума однозначних чисел, виражених його цифрами (сума цифр) а_n +... + a₁ + a₀, ділилася на 3 або на 9. Теорему доведено.

8. Загальна ознака подільності Паскаля

У XVII ст. відомий французький математик Б. Паскаль довів загальну ознаку подільності, яка доводиться для чисел, записа­них у будь-якій позиційній системі числення. Сформулюємо й доведемо її для натуральних чисел, записаних у десятковій системі числення.

Теорема (ознака подільності Паскаля). Для того щоб число а_n+…а₀ ділилося на число m, необхідно й достатньо, щоб на число т ділилося число r= a_nr_n+…+a₁r₁+a₀, де rn — остача від ді­лення 10^k на число m, k = 1, 2,..., п.

Доведення. Запишемо число a у вигляді а =a_n10ⁿ +... +a₁10 + а₀ = mq_k + г_k, 0 < r_k < m, k = 1, 2,..., п. Піс­ля підстановки цих значень у запис числа а дістанемо: a = (a_nq_n+ …+ a₁q₁)m + a_nr_n + … + a₁r₁ + a₀).

Теорему доведено.

Наведемо приклад застосування цієї ознаки для m = 11. Маємо 10 = 11-1; 10² = 11 · 9 + 1; 10³ = 11. 91 - 1; 10⁴ =11. 99 +1, ….

Oтже, число а = а_n...а₁a₀ ділиться на 11 тоді і тільки тоді, коли різниця між сумою цифр, які стоять на непарних місцях, і су­мою цифр, які стоять на парних місцях, ділиться на 11, тобто число r = (а₀ + а₂ + …) — (a₁+a₃+...) ділиться на 11.

Так, число 6 671 829 ділиться на 11, бо число r = (9 + 8 + 7 + 6) - (2 + 1 + 5) = 30 – 8 = 22 ділиться на 11.

 

РЕКОМЕНДОВАНА ЛІТЕРАТУРА

1. Курс математики. Навч. посібник. В. Н. Боровик. – К.: Вища шк.1995р. с. 156-161.

2. Основы начального курса математики. Учеб. пособие. Л. П. Стойлова. – М. Просвещение. 1988 г. с. 197 - 206.

3. Математика. Множини. Логіка. Цілі числа. Практикум. В. М. Кухар. – К. Вища школа. 1989 р. с. 275 – 281, 277-278.

Практичне заняття № 2

Тема. Подільність чисел. Застосування ознак подільності суми, різниці, добутку цілих невід’ємних чисел

Мета. Пригадати теоретичні відомості про подільність чисел та застосувати їх до розв’язування задач.

Студенти повинні знати:

· поняття відношення подільності;

· символ для позначення відношення “ділитись націло”;

· означення простого і складеного числа;

· властивості відношення подільності;

· ознаки подільності суми, різниці, добутку цілих невід’ємних чисел.

Студенти повинні вміти:

· виконувати ділення одного числа на інше з остачею і націло;

· доводити ознаки подільності;

Література

1. Курс математики: Навч. посібник / В. Н. Боровик. – К.: Вища шк., 1995. с. 156-158, 170-171.

2. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1980. с. 153-154, 157-161.

3. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1987. с. 192 -199.

4. Основы начального курса математики: Учеб. пособие Л. П. Стойлова. - М. “Просвещение” 1988. с. 197-203, 206-215.

5. Математика. Множини. Логіка. Цілі числа. Практикум. В. М. Кухар. – К. Вища шк., с. 1989. с. 275-283, 286-294.

План та хід заняття

І. Актуалізація опорних знань

1. Що означає число а поділити на число b без остачі?

2. Яким символом позначається відношення подільності і чи відрізняється цей символ від дії ділення?

3. Чому не можна будь-яке число поділити на нуль? Чому не можна нуль ділити на нуль?

4. Яке число називається простим, а яке складеним?

5. Назвіть властивості відношення подільності.

6. Сформулюйте і доведіть теореми про подільність суми, різниці, добутку.

7. Доведіть теорему про подільність суми для: 1) трьох доданків; 2) m доданків.

8. Доведіть теорему про подільність різниці цілих невід’ємних чисел на натуральне число.

9. Відомо, що а не кратне n і b не кратне n. Чи правильно, що: 1) не кратне n; 2) не кратне n?

 

ІІ. Розв’язування вправ

1. Чому число 15 є дільником числа 60; кратним числа 3? Відповідь обґрунтуйте.

2. Які із чисел 2, 3, 5 є дільниками чисел 230; 225; 450?

3. Які із чисел 804, 75, 144, 150 є кратними 2; 3; 5; 9?

4. Назвіть п’ять чисел, кратних 3. За якою формулою можна одержати інші числа, кратні 3?

5. Запишіть множину дільників чисел: 24; 38; 13; 1.

6. Множина цілих невід’ємних чисел в залежності від остачі при діленні на два розбивається на два класи. Із яких чисел складається кожний із цих класів? Назвіть по два представники кожного класу. Яка формула дає можливість одержати всі парні числа, а яка непарні?

7. Поясніть, чому число 19 просте, а число 18 – складене.

8. При яких значеннях q значення виразу 11q є простим числом?

9. Запишіть всі прості дільники числа 60.

10. Серед даних висловлень назвіть істинні:

а) множина натуральних чисел розбивається на клас простих чисел і клас і клас складених;

б)множина натуральних чисел складається із простих чисел, складених чисел і числа 1.

11. Побудуйте граф відношення “число x – дільник числа y ” на множині X = {12, 9, 6, 3,18}. Які особливості цього графа? Чим від нього буде відрізнятися граф відношення “ x кратне y”, якщо відношення задано на тій же множині.

12. Чи кратна числу 4 сума двох послідовних а) парних чисел; б) непарних чисел.

13. Відомо, що і . Який висновок можна зробити про подільність числа а на 2?

14. Які остачі можуть бути отримані при діленні а на 3? Який вигляд чисел, які на 3 не діляться?

15. А – множина цілих невід’ємних чисел виду 3q, В – множина цілих невід’ємних чисел виду 3q+1, С – множина цілих невід’ємних чисел виду 3q+2. Чи можна стверджувати, що ?

16. З множини цілих невід’ємних чисел виділили підмножину чисел, кратних 7. Розбийте будь-яким чином на класи підмножину чисел, не кратних 7. Скільки класів розбиття множини отримали?

17. Не виконуючи додавання, встановіть, чи ділиться значення виразу на 3:

1) 180+144; 2) 720+308; 3) 103+370.

18. Не виконуючи віднімання, вкажіть вирази, значення яких ділиться на 5: 1) 535-413; 2) 1215-470; 3) 20 147-1 307.

19. Не виконуючи обчислень, встановіть, чи буде добуток ділиться на 5, 8, 9, 10, 18, 45.

20. Якщо до двоцифрового числа додати число, записане тими ж цифрами, але в зворотньому порядку, то сума буде кратна 11. Доведіть це.

21. Доведіть, що добуток трьох послідовних натуральних чисел ділиться на 3.

22. Доведіть, що квадрат непарного натурального числа при діленні на 8 дає остачу 1.

23. Доведіть, що сума квадратів двох послідовних натуральних чисел при діленні на 4 дає остачу 1.

24. Записати числа виду , які діляться на 4. (Відповідь: 13752; 13756).

25. Скільки чисел виду 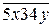діляться на 4?

Розв’язок. Розглянемо число , де замість y будемо послідовно підставляти цифри, так щоб утворене двозначне число ділилось на 4. Отримаємо: 40 – ділиться на 4; 40+4=44 – ділиться на 4; 44+4=48 – ділиться на 4. Отже, кожне з трьох чисел , та при довільному значенні x ділиться на 4. У кожному з них x може приймати будь-яке з 10 значень від 0 до 9. Тому маємо 3×10=30 чисел.

Відповідь: 30 чисел.

26. Доведіть, що сума і різниця квадратів двох послідовних натуральних чисел завжди непарні числа, а добуток цих квадратів ділиться на 4.

 

ІІІ. Завдання для самостійного виконання

Варіант 1

1. Запишіть усі числа, кратні 5, які задовольняють нерівності 570 < b < 581.

Відповідь поясніть.

 

2. Не виконуючи додавання, вияснити, чи ділиться сума: а) 124+420+213 на 4; б) 1080+123+124 на 9.

 

3. Який з добутків чисел 243 ∙ 42 чи 123 ∙ 42 ділиться на 9?

4. Записати усі числа виду , що діляться на 4.

 

5. Довести, що добуток двох послідовних парних чисел ділиться на 8.

 

Варіант 2

1. Запишіть усі числа, кратні 2, які задовольняють нерівності 572 b < 585.

Відповідь поясніть.

2. Не виконуючи додавання, вияснити, чи ділиться сума: а) 124+420+213 на 5; б) 1080+123+124 на 3.

 

3. Який з добутків чисел 244 ∙ 25 чи 122 ∙ 42 ділиться на 4.

 

4. Записати усі числа виду , що діляться на 4.

 

5. Довести, що різниця між трицифровим числом і числом, записаним тими ж цифрами, але взятими в зворотному порядку, діляться на 9.

 

 

Варіант 3

1. Запишіть усі числа, кратні 9, які задовольняють нерівності 570 < b 585.

Відповідь поясніть.

2. Не виконуючи додавання, вияснити, чи ділиться сума: а) 256+184+231 на 3; б) 156+236+216 на 4.

 

3. Який з добутків чисел 256·36 чи 126·33 ділиться на 6.

 

4. Скільки чисел виду діляться на 4?

 

5. Довести, що різниця між кубом будь-якого числа і самим числом ділиться на 6.

Варіант 4

1. Запишіть усі числа, кратні 3, які задовольняють нерівності 270 < b < 281.

Відповідь поясніть.

2. Не виконуючи додавання, вияснити, чи ділиться сума: а) 438+246+178 на 2; б) 225+658+355 на 5.

 

3. Який з добутків чисел 144·29 чи 561·56 ділиться на 12.

 

4. Скільки чисел виду діляться на 4?

 

5. Довести, що трицифрове число, записане однаковими цифрами, ділиться на 37.

ІV. Підсумок. Домашнє завдання

1. Найбільший спільний дільник і найменше спільне кратне

Раніше ми знаходили дільники лише одного числа. Часто виникає необхідність знати спільні дільники двох і більше натуральних чисел, зокрема при додаванні і відніманні звичайних дробів.

Візьмемо два числа. 12 і 18. Дільники числа 12 є: 1, 2, 3, 4, 6, 12, а числа 18 – 1, 2, 3, 6, 9, 18. Спільні дільники чисел 12 і 18: 1, 2, 3, 6. Серед них є найбільший дільник – число 6. Його називають найбільшим спільним дільником чисел 12 і 18.

Означення. Спільним дільником натуральних чисел a і b називається натуральне число, яке є дільником кожного з даних чисел.

Означення. Найбільшим спільним дільником натуральних чисел а і b називається найбільше число з усіх спільних дільників даних чисел і позначається НСД (а, b) або Д(а, b).

Аналогічно означується поняття найбільшого спільного дільника для кількох натуральних чисел. Так, Д(12, 48, 24) = 12.

Найбільший спільний дільник має такі найпростіші властивості.

1. Для будь-яких натуральних чисел а і b існує єдиний НСД. Справді, множина спільних дільників чисел а і b непорожня, бо вона має принаймні число 1, крім того, вона скінчена. Тому серед її елементів знайдеться єдине число, яке є НСД (а, b).

2. НСД (а, b) не перевищує меншого з даних чисел, тобто якщо а < b, то

НСД(а, b) £ а.

3. НСД (а, b) ділиться на будь-який їхній спільний дільник. Справді, нехай

НСД (а, b) = d, а d₁ – будь-який їхній спільний дільник. Тоді а = dq, b = dq₁ , де числа q i q₁ мають спільним дільником тільки 1. Отже, спільний дільник d₁ чисел а і b є дільником їхнього найбільшого спільного дільника d.

Якщо а M b, то НСД (а, b) = b.

Означення. Якщо НСД (а₁, а₂, …, а_k) = 1, то числа а₁, а₂, …, а_k називаються взаємно простими. Якщо, крім того, кожна пара цих чисел взаємно проста, то числа а₁, а₂,.., а_k називаються попарно взаємно простими.

Так, числа 4, 6, 7 – взаємно прості, НСД (4, 6,7) = 1. Проте, вони не є попарно взаємно простими, НСД (4, 6) = 2. Отже, попарно взаємно прості числа є взаємно простими, але обернене твердження, взагалі кажучи, не справджується.

Як відомо, число а є кратним числа b, якщо а M b, або а = bq. Очевидно, нуль є кратним будь-якого числа, тому далі розглядатимемо лише натуральні числа.

Візьмемо числа 12 і 18. Кратними числа 12 є 12, 24, 36,… а кратними числа 18 – 18, 36, 54,… Числа 12 і 18 мають спільні кратні: 36, 72, … Серед них є найменше кратне - число 36. Його називають найменшим спільним кратним чисел 12 і 18.

Означення. Спільним кратним натуральних чисел а і b називається натуральне число, кратне кожному з даних чисел.

Означення. Найменшим спільним кратним натуральних чисел а і b називається найменше число з усіх спільних кратних даних чисел.

Найменше спільне кратне чисел а і b Позначається НСК (а, b) або К (а, b). Так, К (12, 18) = 36.

Найменше спільне кратне має такі найпростіші властивості:

1. Для будь – яких натуральних чисел а і b існує єдине найменше спільне кратне.

Справді, множина спільних кратних даних чисел непорожня, бо вона містить добуток даних чисел. За принципом найменшого числа у множині спільних кратних існує найменше число. Це число і є найменшим спільним кратним даних чисел.

2. Найменше спільне кратне чисел а і b не менше більшого з даних чисел, тобто якщо a > b, то НСК (а, b) ³ а.

3. Кожне спільне кратне даних чисел а і b ділиться на найменше спільне кратне цих чисел.

Справді, нехай М – довільне спільне кратне чисел а і b, m = НСК (a,b). За теоремою про ділення з остачею М = mq + r, де 0 £ r < m. За умовою числа m i М ділиться на а і b, отже, і число r = М – mq теж ділиться на кожне з них. Проте, при r < m це можливо лише тоді, коли r = 0. Таким чином, М = mq.

4. Якщо а M b, то НСК (а, b) =а.

 

2. Обчислення найбільшого спільного дільника і найменшого спільного кратного за канонічним розкладом чисел

 

Теорема. НСД (а,b) є найменшим спільним кратним усіх спільних дільників чисел а і b.

Нехай треба знайти НСД і НСК двох чисел 360 і 525. За основною теоремою арифметики ці числа можна подати однозначно у канонічному вигляді.(Будь-яке натуральне число, більше 1, може бути розкладене в добуток простих співмножників. Цей розклад є єдиним, якщо не враховувати порядок слідування співмножників.)

360 = 2³×3²×5; 525 = 3×5²×7. У розклад на прості множники НСД цих чисел повинні ввійти всі спільні прості множники, причому кожний з них треба взяти з найменшим показником, з яким він входить в канонічні розклади даних чисел. Отже, НСД (360, 525) = 3×5 = 15.

У розклад на прості множники НСК (360, 525) повинні ввійти всі прості множники, які входять принаймні в один розклад, причому кожний з них треба взяти з найбільшим показником. НСК (360, 525) = 2³ × 3² × 5² × 7 = 12600.

За аналогічним правилом знаходять НСК і НСД будь-яких двох чисел.

Теорема. НСД(а, b) × НСК(а, b) = а × b.

Наслідок. Якщо НСД(а, b) = 1, то НСК(а, b) = аb.

Таким чином, НСК двох чисел дорівнює добутку цих чисел тоді і тільки тоді, коли ці числа взаємно прості.

Щоб знайти НСД натуральних чисел за їхнім канонічним розкладом, треба спочатку розкласти ці числа на прості множники. Для великих чисел це складна задача. З часів Евкліда (ІІІ ст. н. е.) відомий більш ефективний спосіб знаходження НСД, який оснований на діленні з остачею і називається алгоритмом Евкліда.

Лема 1. Якщо а M b, то НСД(а, b) = b.

Лема 2. Якщо a = bq + r, де a, b, r – натуральні числа, то НСД(а, b) = НСД(b, r).

Покажемо, що сукупність спільних дільників а і b збігається з множиною дільників b і r то d буде спільним дільником а = bq + r і b. Справедливе й обернене, якщо d – спільний дільник а і b, то d є дільником і числа r = a – bq, a отже, спільним дільником чисел b i r. Таким чином, множина спільних дільників чисел а і b збігається з множиною спільних дільників b i r. Тому вони мають один і той самий найбільший дільник. Отже, НСД(а, b) = НСД(b, r). Лему доведено.

3. Алгоритм Евкліда

Розглянемо алгоритм Евкліда для знаходження НСК довільних натуральних чисел а і b. Нехай а ³ b. Якщо а M b, то за лемою 1 НСД(а, b) = b. Якщо а = bq + r, де r ¹ 0, то за лемою 2 задача знаходження НСД зводиться до обчислення НСД чисел b i r, де r < b. Якщо b M r, то НСД(b, r) = r, а отже, і НСД(а, b) = r. Якщо при діленні b на r матимемо остачу 0 < r₁ < r, то b = rq₁ + r₁, і тому НСД(а, b) = НСД(b, r) = НСД(r, r₁). Продовжуючи описаний процес, діставатимемо все менші і менші остачі: r, r₁, … r_m. З рештою дістанемо остачу, яка ділить попередню остачу. Згідно з лемою 2, ця, відмінна від 0, остача і є НСД(а, b).

Таким чином, доведено теорему: НСД двох натуральних чисел дорівнює останній, відмінній від нуля остачі в алгоритмі Евкліда для цих чисел.

Алгоритм Евкліда як спосіб послідовного ділення зручно записувати у вигляді многократного ділення кутом.

Приклад. Знайдемо НСД(90, 35).

90 35 Таким чином,

70 2 90 = 35 × 2 + 20

35 20

20 1 35 = 20 × 1 + 15

20 15

15 1 20 = 15 × 1 + 5

15 5

15 3 15 = 5 × 1 + 0

Отже, остання відмінна від нуля остача дорівнює 5, тому НСД(90,35) = 5.

Позначимо 90 через а, 35 – через b. Рівність 20 = 15 × 1+ 5 запишемо так: 5 = 20 – 15 × 1. З попередньої рівності знайдемо: 15 = b – 20 × 1. Підставимо це значення 15 у вираз 5 = 20 – 15 × 1. Дістанемо: 5 = 20 –(b – 20 × 1)×1. З рівності: 90=35 × 2 + 20 запишемо 20 =а – b × 2. Підставимо це значення у попередній вираз. Тоді 5 = а – b × 2-(b - (a – b × 2) ×1). Після виконання обчислень матимемо: 5= а × 2 + b × (-5). Отже, d=ax - by.

З алгоритма Евкліда випливає таке твердження: для будь-яких двох натуральних чисел а і b знайдуться такі натуральні числа x i y, що НСД(а, b) = ax – by.

На основі цього твердження можна дійти висновку про те, що коли d = НСД(a,b), то рівняння виду d = ax – by завжди розв’язне у множині цілих чисел.

Рівність НСД(a,b) = ax – by має велике значення для доведення багатьох властивостей про натуральні числа. Для прикладу доведемо таке твердження: якщо добуток натуральних чисел ділиться на просте число, то принаймні один із множників ділиться на це просте число.

Справді, нехай добуток ab натуральних чисел a i b ділиться на просте число p. Припустимо, що а не ділиться на p. Тоді НСД(а, p) =1. Отже, знайдуться такі числа x i y, що 1 = ax + py. Помножимо дану рівність на число b. Дістанемо: b = abx + pby. Як бачимо, кожний з доданків суми ділиться на р, тому й b M p.

Після обчислення за допомогою алгоритма Евкліда НСД двох чисел, можна знайти їхнє НСК, використовуючи залежність між НСД і НСК. Так, НСК(90, 35) = 90 × 35: 5 = 630.

Алгоритм Евкліда є тим загальним методом, за яким через скінчене число кроків можна обчислити НСД і НСК будь-яких двох і більше натуральних чисел.

 

4. Ознака подільності на складені числа

Доведені ознаки дають змогу визначити подільність чисел на 2, 3, 4, 9.

Сформулюємо ознаки подільності на 8, 25 і 11:

Число а ділиться на 8 тоді й тільки тоді, коли а ₂ а ₁ а ₀ ділиться на 8.

Число а ділиться на 25 тоді і тільки тоді, коли а ₁ а ₀ ділиться на 25.

Число а ділиться на 11, якщо різниця цифр, що стоять на парних і непарних місцях, ділиться на 11. Наприклад. Чи ділиться число 256 375 на 11?

(5 + 3 + 5) – (7 + 6 + 2) = - 2. – 2 не M на 11. Значить 256 375 не M на 11.

Розглянемо ознаки подільності на складені числа.

Теорема. (ознаки подільності на 6) Для того щоб число а ділилося на 6, необхідно й достатньо, щоб воно ділилося на 2 і 3.

Доведення. Необхідність. Дано а M 6. Довести, що а M 2 і а M 3.

Нехай а M 6. Тоді оскільки а M 6 і 6 M 2, то а M 2. Через те що а M 6 і 6 M 3, то

а M 3.

Достатність. Дано: а M 2 і а M 3. Довести: а M 6.

Якщо а M 2 і а M 3, то а – спільне кратне чисел 2 і 3, а будь-яке кратне чисел ділиться на їхнє НСК. Отже, а M К(2,3). Оскільки Д(2, 3) = 1, то К(2, 3) = 2 × 3 = 6. Таким чином, а M 6. Теорему доведено.

Теорема. (ознаки подільності на 12) Для того щоб число а ділилося на 12, необхідно й достатньо, щоб воно ділилося на 3 і 4.

Доведення цієї теореми аналогічне попередній.

Теорема. (ознаки подільності на 15) Для того щоб число а ділилося на 15, необхідно й достатньо, щоб воно ділилося на 3 і 5.

Список ознак подільності на складені числа можна продовжити. Їх узагальненням є теорема:

Теорема. (Ознака подільності на складені числа). Для того щоб натуральне число ділилось на складене число n = bc, де числа b і c такі, що Д (b, c) = 1, необхідно і достатньо, щоб воно ділилось на b і на c.

Доведення цієї теореми проводиться аналогічне доведенню ознаки подільності на 6.

Розглянемо ознаку подільності на 60. Для того щоб число ділилось на 60, необхідно і достатньо, щоб воно ділилось на 4 і на 15.

Але, в свою чергу, число ділиться на 15 тоді й тільки тоді, коли воно ділиться на 3 і на 5. Тому ознаку подільності на 60 можна сформулювати так:

Для того, щоб число ділилось на 60, необхідно й достатньо, щоб воно ділилось на 4, на 3 і на 5.

Задача. Встановити, чи діляться числа 1548 і 942 на 18.

Сформулюємо спочатку ознаку подільності на 18:

Для того щоб число ділилось на 18, необхідно і достатньо, щоб воно ділилось на 2 й на 9.

Чому вибрано числа 2 і 9? По-перше, 2 × 9 = 18, а по-друге, Д (2, 9) = 1, тобто числа 2 і 9 задовольняють теорему про подільність на складені числа.

Представлення 18 у вигляді 3 × 6 не підходить, тому що Д (3, 6) ¹ 1.