Користуючись ознаками подільності на 2 і на 9, стверджуємо, що 1548 M 2 і 1548 M 9. Отже, 1548 M 18.
Число 942 M 2, але воно не ділиться на 9. Тому число 942 не ділиться на 18.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Курс математики. Навч. посібник. В. Н. Боровик. - К.: Вища шк. 1995 р. с. 164-171.
2. Основы начального курса математики. Учеб. пособие. Л. П. Стойлова. – М. Просвещение. 1988 г. с. 208- 215.
3. Математика. Множини. Логіка. Цілі числа. Практикум. В. М. Кухар. – К. Вища школа. 1989 р. с. 279, 286-294.
Практичне заняття № 3
Тема. Знаходження найбільшого спільного дільника і найменшого спільного кратного натуральних чисел. Модульний контроль.
Мета. Узагальнити та систематизувати теоретичні відомості про найбільший спільний дільник і найменше спільне кратне та їх властивості і застосувати до розв’язування вправ.
Студенти повинні знати:
· означення та властивості найбільшого спільного дільника та найменшого спільного кратного;
· алгоритм Евкліда для знаходження найбільшого спільного дільника чисел.
Студенти повинні вміти:
· знаходити найбільший спільний дільник і найменше спільне кратне двох, кількох чисел.
Література
1. Курс математики: Навч. посібник / В. Н. Боровик. – К.: Вища шк., 1995. с.
156-158, 170-171.
2. Теоретичні основи початкового курсу математики: Навч. посібник / В. М.
Кухар. – К. Вища шк., 1980. с. 153-154, 157-161.
1. Теоретичні основи початкового курсу математики: Навч. посібник / В. М.
Кухар. – К. Вища шк., 1987. с. 192 -199.
2. Основы начального курса математики: Учеб. пособие Л. П. Стойлова. - М. “Просвещение” 1988. с. 197-203, 206-215.
3. Математика. Множини. Логіка. Цілі числа. Практикум. В. М. Кухар. – К. Вища шк., с. 1989. с. 275-283, 286-294.
План та хід заняття
І. Актуалізація опорних знань
1. Сформулюйте означення спільного кратного, найменшого спільного кратного для двох чисел, його властивості та способи знаходження.
2. Сформулюйте означення спільного дільника, найбільшого спільного дільника для двох чисел, його властивості та способи знаходження.
ІІ. Розв’язування вправ
1. Знайдіть найбільший спільний дільник і найменше спільне кратне чисел: 1) 175 і 245; 2) 540 і 558; 3) 120 і 80; 4) 675 і 154.
2. Знайдіть найменше спільне кратне чисел а і b, якщо відомо, що: 1) Д(315, 385) = 35; 2) Д(47, 105) = 1.
3. Знайдіть найменше спільне кратне всіх однозначних парних чисел.
4. Найбільший спільний дільник двох чисел, одне з яких 600, дорівнює 120.
Найменше спільне кратне цих же чисел дорівнює 4800. Знайдіть друге число.
5. Знайти НСК(340, 5440, 510) і НСД (340, 5440, 510).
6. Використовуючи алгоритм Евкліда, знайти НСД (6253, 1001) та НСК (6253, 1001) чисел.
7. Найбільший спільний дільник двох чисел – 27, а їхнє найменше спільне кратне 324. Знайти ці числа, якщо одне з них становить 3/4 іншого.
8. Турист в перший день проїхав на велосипеді 80 км, а в другий – 64, а в третій – 96 км. Скільки годин велосипедист був у дорозі за три дні, якщо швидкість його була однакова і найбільша з можливих? (Вказівка. Швидкість – НСД(80, 64, 96).
9. Довжина кола переднього колеса екіпажа 2 м 25 см, заднього – 3 м 25 см. Знайти найменшу відстань, яку повинен проїхати екіпаж, щоб переднє і заднє колеса зробили по цілому числу обертів.
10. Троє суден заходять в порт після кожного рейсу. Перше судно проходить свій рейс за 6 днів, друге – за 5, третє – за 10 днів. Через скільки днів (найменше) зустрінуться в порту перше судно з другим, перше з третім, друге з третім і всі троє разом, якщо вони вийшли в рейс одночасно?
11. Знайти числа а і b, якщо а + b = 168, НСД(а, b) = 24.
12. У порту пришвартувалося 4 теплоходи. Опівдні 2 січня 1983 року вони одночасно зайшли в порт. Відомо, що перший теплохід повертається до цього порту через кожні 4 тижні, другий – через 8 тижнів, третій – через 12 тижнів, а четвертий – через 16 тижнів. Коли вперше теплоходи знов зустрінуться в цьому порту?
13. Довести, що добуток чотирьох послідовних чисел ділиться на 24, а добуток п’яти послідовних чисел ділиться на 120.
14. Довести, що різниця між кубом будь-якого числа і самим числом ділиться на 6, а різниця між кубом непарного числа і самим числом ділиться на 24.
15. Яке найбільше число неділь може бути за рік?
16. Знайти НСД(а, b), якщо:
а) а = 120, b = 144;
б) a = 275, b = 180;
ІІІ. Завдання для самостійного виконання (тести)
Варіант 1
| № п/п | Запитання | Варіанти відповідей |
| Розкладом числа 234 на прості множники є: | А. 22·3·7; Б. 32·5·7; В. 2·3·5·13; Г. 2·32·13. | |
| Найменшим числом, кратним даному числу n є: | А. n – 1; Б. n; В. 3n; Г. n:2. | |
| Кількість дільників числа 90, які є простими числами, дорівнює: | А. 4; Б. 5; В. 3; Г. 6. | |
| Парним називається число, яке: | А. ділиться на 2; Б. більше від 2; В. закінчується нулем; Г. ділиться на 2 або 5. | |
| Є 87 синіх і 116 червоних олівців. Найбільша кількість комплектів, які можна скласти з цих олівців, щоб у всіх комплектах було однакове число синіх і однакове число олівців, дорівнює: | А. 17; Б. 29; В. 43; Г. 58. | |
| На 4 не ділиться число: | А. 12345628; Б. 7030844; В. 2564097; Г. 1020304. | |
| З кінцевої зупинки одночасно виїжджають за різними маршрутами два тролейбуси. Тривалість маршруту першого тролейбуса 39 хв., а другого – 1 год. 5 хв. Після виїзду тролейбуси знову зустрінуться на кінцевій зупинці через: | А. 3 год.25хв.; Б. 2 год.45хв.; В. 3 год.15хв.; Г. 4 год.20хв. | |
| Щоб число 23*91 було кратне 9, замість * необхідно записати цифру: | А. 0; Б. 1; В. 3; Г. 9. | |
| Взаємно простими є числа: | А. 615 і 390; Б. 25 і 170; В. 12 і 27; Г. 14 і 33. | |
| Найбільшим трицифровим числом, яке складається з різних цифр і одночасно ділиться на 5 і на 9 є число: | А. 981; Б. 945; В. 985; Г. 890. |
Варіант 2
| № п/п | Запитання | Варіанти відповідей |
| Усі дільники числа 18 – це числа: | А. 2, 3, 6, 18; Б. 1, 2, 3, 6, 18; В. 1, 2, 3, 4, 6, 12; Г. 18, 36, 54. | |
| Дільниками числа 2·5·11 є числа: | А. 1,2,5,10,11,22,55,110; Б. 1,2,5,7,10,22,55; В. 2,5,10,11,22,55; Г. 110,220,330. | |
| Спільними дільниками чисел 16 і 24 є числа: | А. 2, 3, 4, 6, 8, 12; Б. 2, 3, 4; В. 48, 96, 144; Г. 1, 2, 4, 8. | |
| Найбільшим спільним дільником чисел 28, 84 і 98 є число: | А. 28; Б. 14; В. 7; Г. 2. | |
| На 3 і 5 ділиться число: | А. 84650791; Б. 7342510; В. 941028; Г. 64305. | |
| Відомо, що а=2·32·5, b=2·3·52. Тоді НСД(а;b) дорівнює: | А. 45; Б. 6; В. 10; Г. 30. | |
| Простим називається число, яке: | А. ділиться на 2; Б. не ділиться на 2; В. має тільки два різні дільники; Г. має тільки один дільник. | |
| Хлопчик розтавив книжки порівну на 14 полицях, а потім переставив їх, теж порівну, на 8 полицях. Якщо відомо, що у хлопчика книжок більше за 100 і менше від 124, то книжок: | А. 120; Б. 122; В. 116; Г. 112. | |
| Взаємно простими є числа: | А. 615 і 390; Б. 25 і 170; В. 12 і 27; Г. 14 і 33. | |
| Найбільший спільний дільник чисел 12,15 і 18 менше від найменшого спільного кратного цих чисел у: | А. 60 разів; Б. 10 разів; В. 50 разів; Г. 20 разів. |
ІV. Підсумок. Домашнє завдання
МОДУЛЬ 4
1. Поняття дробу
Історично виникнення дробів зв’язано з вимірюванням величин. З’ясуємо, як, наприклад, можуть з’явитися дроби при вимірюванні довжини відрізка.
Візьмемо відрізок а. щоб знайти його довжину візьмемо в якості одиниці довжини відрізок е. При вимірюванні виявилось, що довжина відрізка а 
більше 3 е, але менше 4 е, тому її не можна виразити натуральним числом.
Але якщо розбити відрізок е на 4 рівні частини, кожна з яких рівна 
, то довжина відрізка а виявиться рівною 14 . Якщо ж повернутися до вихідної одиниці е, то ми повинні сказати, що відрізок а складається з 14 відрізків, рівних четвертій частині відрізка е, тобто, говорячи про довжину відрізка а, ми повинні оперувати двома натуральними числами 14 і 4. домовились в такій ситуації довжину відрізка записувати у вигляді 
, а символ 
називати дробом.
Означення. Нехай дано відрізок а і одиничний відрізок е, причому відрізок е являється сумою п відрізків, рівних . Якщо відрізок а складається з т відрізків, рівних , то його довжина може бути представлена у вигляді 
. Символ 
називають дробом, т і п – натуральні числа.
Повертаючись до нашого прикладу варто сказати, що ми могли взяти, наприклад, восьму частину відрізка е, яка вміщується ціле число раз у відрізок а. тоді його довжина буде рівна 
. Можна взяти шістнадцяту частину відрізка е, тоді відрізок а буде складатись з 56 таких частин і його довжина буде рівна 
і т. д.
Означення. Дроби, що виражають довжину одного і того ж відрізка при одиниці довжини е, називають рівними дробами.
Ознака рівності дробів: для того щоб дроби і 
були рівними, необхідно і досить, щоб 
.
Основна властивість дробу: якщо чисельник і знаменник дробу помножити або поділити на одне і те ж натуральне число, то отримаємо дріб, що дорівнює даному.
Скорочення дробів – це заміна даного дробу іншим, що дорівнює даному, але з меншим чисельником і знаменником.
Дріб у якого чисельник і знаменник взаємно прості, називається нескоротним.
Зведення дробів до спільного знаменника – це заміна дробів рівними їм дробами, що мають однакові знаменники. Спільним знаменником двох дробів є спільне кратне їх знаменників, а найменшим спільним знаменником – їх найменше спільне кратне.
Відношення рівності дробів є відношенням еквівалентності.
2. Додатні раціональні числа. Алгебраїчні операції над раціональними числами
О значення. Додатне раціональне число – це множина рівних між собою дробів, а кожен дріб, що належить цій множині, є записом (зображенням) цього числа. Множина додатних раціональних чисел позначається 
, 
Теорема. Для будь – якого додатного раціонального числа існує один і тільки один нескоротний дріб, що зображує це число.
Означення. Якщо додатні раціональні числа а і b зображуються дробами і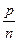 
, то сумою чисел а і b називається число, що зображується дробом 
.
Теорема. Для будь – яких додатних раціональних чисел а і b їхня сума а + b існує і при тому єдина.
Властивості операції додавання раціональних чисел:
Комутативність 
;
Асоціативність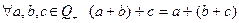 
.
Дріб 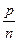називають правильним, якщо 
, і неправильним – якщо 
. Якщо 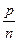- неправильний дріб, то: 
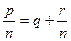, де q – ціла частина дробу (натуральне число), 
- правильний дріб.
Будь – який неправильний дріб, в якому чисельник не кратний знаменнику, можна зобразити єдиним чином у вигляді суми його цілої частини та правильного дробу з тим самим знаменником, що й даний неправильний дріб. Цю операцію називають виділенням цілої частини з неправильного дробу.
Означення. Нехай а і b – додатні раціональні числа. Тоді а менше b, якщо існує таке додатне раціональне число с, що а+с=b.
Означення. Різницею додатних раціональних чисел а і b називають таке додатне раціональне число с, що с+b=а.
Теорема. нехай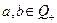 
, різниця а – b існує тоді і тільки тоді, коли 
. Якщо різниця існує, то вона єдина.
Означення. Якщо додатні раціональні числа зображені дробами і , то їх добуток є число, що зображується дробом 
.
Теорема. Для будь – яких додатних раціональних чисел а і b існує добуток аb і при тому єдиний.
Властивості множення:
Комутативність 
Асоціативність 
Дистрибутивність відносно додавання 
Монотонність 
Означення. Часткою двох додатних раціональних чисел а і b називається таке число с, що 
.
Нехай 
, 
. Покажемо, що число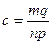 
і є часткою.
За означенням частки а = bc =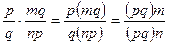 
.
Скоротимо одержаний дріб на натуральне число pq:
.
Отже, частку двох раціональних чисел знаходять за формулою:
а:b= 
.
Риску дробу в записі 
можна розглядати як знак дії ділення m: n.
Термін «раціональне число» виник від латинського слова ratio, що в перекладі на українську мову означає «відношення» (частка).
3. Десяткові дроби
В практичній діяльності людина користується десятковою системою числення. Нові одиниці величин одержують із стандартних, зменшуючи їх в 10, 100, 1000 і т.д. разів. Тому для практики важливо мати ці дроби, знаменники яких є степенями числа 10. Наприклад 
. Такі дроби називаються десятковими.
Порівняння десяткових дробів і виконання дій над ними зводиться до порівняння і виконання дій над натуральними числами. Наприклад, 0,3472 < 0,3480, так як при однакових десятих і сотих частин тисячних частин у першого числа менше, ніж у другого.
Чи будь-який звичайний дріб можна перетворити в десятковий?
Теорема. Для того, щоб нескоротний дріб дорівнював десятковому дробу, необхідно і достатньо, щоб в розкладі його знаменника на прості множники входили лише числа 2 або 5.
Прпиклад. 
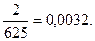
Серед десяткових дробів виділяють дріб 0,01. Його називають відсотком і позначають 1%. На практиці використовують це так: ціни на товари знизились на 20%, цукрова тростина містить 15% цукру.
Розрізняють скінченні десяткові дроби і нескінченні десяткові дроби. З нескінченних десяткових дробів виділяють періодичні і неперіодичні, чисті періодичні – в них період починається зразу після коми і змішані періодичні дроби – в них між комою і періодом є інші десятизначні знаки. Наприклад, 0,(857142) – чистий періодичний дріб, а 3,27(346) – змішаний періодичний дріб.
Теорема. Якщо дріб 
нескоротний і в розкладі знаменника на прості множники є простий множник відмінний від 2 і 5, то дріб подається у вигляді нескінченного періодичного дробу.
Щоб записати додатне раціональне число у вигляді нескінченного періодичного дробу, потрібно чисельник поділити на знаменник.
Як виконати обернене перетворення?
Теорема. Чистий періодичний нескінченний десятковий дріб дорівнює такому звичайному дробу, в якого чисельник дорівнює періоду, а знаменник містить стільки дев’яток, скільки цифр в періоді дробу.
0,282828…= 
Змішаний періодичний дріб з нулем в цілій частині дорівнює такому звичайному дробу, чисельник якого дорівнює різниці між числом, записаним цифрами, які стоять до початку другого періоду, і числом, записаним цифрами, що стоять до початку першого періоду, а знаменник містить стільки дев’яток, скільки цифр в періоді, і стільки нулів, скільки цифр стоїть до початку першого періоду.
0,86161= 
4. Множина додатних ірраціональних чисел. Додатні дійсні числа
Як відомо, дії над додатними раціональними числами зручно виконувати, якщо вони представлені десятковими дробами. Тому слід і результати вимірювання величин, в тому числі і відрізків, представляти у вигляді десяткових дробів.
Нехай а – відрізок, довжину якого слід виміряти, відрізок е – одиниця довжини. І нехай відрізок а складається з п відрізків, рівних е, і відрізка 
, який коротший відрізка е, тобто 
. Числа п і п +1 називаються наближеними значеннями відрізка а при одиниці довжини е з недостачею і з надлишком з точністю до одиниці.
Щоб отримати відповідь з більшою точністю, візьмемо відрізок 
- десяту частину відрізка е і спробуємо вмістити його у відрізок . Можливі два випадки:
1) відрізок буде містити 
відрізків . Тоді довжина відрізка а виражається десятковим дробом: 
.
2) відрізок буде складатися з відрізків, рівних , і відрізка 
, який коротший за відрізок . Тоді 
, де 
і 
- наближені значення довжин відрізка а з недостачею і з надлишком з точністю до 0,1.
Зрозуміло, що у випадку 2 можна взяти новий одиничний відрізок 
, і продовжити вимірювання. В даному випадку можливі 2 варіанти:
а) на деякому k – му кроці процес вимірювання закінчиться. Тоді довжина відрізка а виразиться скінченим десятковим дробом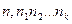 
.
б) описаний процес не скінчений. Тоді довжина відрізка а запишеться у вигляді символу 
, який називають нескінченним десятковим дробом.
Отже, в процесі вимірювання відрізків можна отримати нескінченні десяткові дроби. Причому існують відрізки, довжини яких не можна виразити нескінченними десятковими періодичними дробами (тобто додатними раціональними числами) при даній одиниці довжини.
Покажемо, що коли за одиницю довжини взяти сторону квадрата, то довжина діагоналі цього квадрата не може бути виражена додатнім раціональним числом.
Припустимо супротивне, тобто що довжина діагоналі а квадрата зі стороною е виражається нескоротним дробом : 
. За теоремою Піфагора 
, або 
. Звідси 
. Отже 
(т – парне). Нехай 
. Тоді 
, або 
, отже п – парне число, наприклад 
. Тобто 
. А це суперечить тому, що вихідний дріб нескоротний.
Отримане протиріччя доводить існування відрізків, довжини яких неможливо виразити додатними раціональними числами. Тому виникає необхідність розширити множину додатних раціональних чисел, доповнивши її так званими додатними ірраціональними числами.
Означення. Нескінченний неперіодичний десятковий дріб називають ірраціональним числом.
Згідно з цим, нескінченні неперіодичні десяткові дроби зображують довжини відрізків, несумірних з одиничним відрізком. Оскільки довжина відрізка є число додатне для будь – якого відрізка, то означене вище ірраціональне число називається додатними ірраціональним числом. Множину додатних ірраціональних чисел позначають 
. Дана множина нескінченна.
Означення. Об’єднання множин і називають множиною додатних дійсних чисел і позначають 
. Причому множини і не перетинаються. Множина нескінченна.
Множину можна розглядати як множину нескінченних десяткових дробів, відмінних від 0,00…0… і тих, що є періодичними з періодом 9.
Означення. Нехай задано два додатні числа α і β:
говорять, що число α дорівнює числу β, і пишуть α=β, якщо 
.
говорять, що число α менше від числа β, або число β більше за число α, і пишуть відповідно α<β, або β>α, якщо 
або знайдеться таке натуральне число k, що 
але 
.
Система 
лінійно впорядкована множина, у множині немає ні найменшого, ні найбільшого числа і між будь – якими двома різними додатними дійсними числами міститься безліч додатних раціональних чисел.
