1) менший 22м; 2) більший 17 м?
ІІІ. Самостійне розв’язування вправ
Варіант 1
1 Обгрунтуйте, чи рівносильні рівняння:
1) 
і 
2) 
і 
3) 
і 
4) 
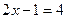і 
2. Знайдіть область визначення та множину розв’язків рівняння
3. Розв’яжіть задачу алгебраїчним способом:
В двох пачках було 30 зошитів. Якщо з першої пачки переклали в другу 2 зошити, то в першій пачці стало в два рази більше зошитів, ніж в другій. Скільки зошитів було в кожній пачці?
4. Знайти найбільше ціле число, яке задовольняє нерівність 
5. Розв'яжіть нерівність 
і поясніть, які теоретичні положення були при цьому використані.
Варіант 2
1. Обгрунтуйте, чи рівносильні рівняння:
1) 
і 
2) 
і 
3) 
і 
4) 
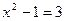і 
2. Знайдіть область визначення та множину розв’язків рівняння
3. Розв’яжіть задачу алгебраїчним способом:
У більший бідон вміщається на 2 л молока більше, ніж у менший. А в два більших бідони вміщається стільки молока, скільки в три менших бідони. Скільки літрів молока входить у більший та менший бідони окремо?
4. При яких цілих значеннях 
значення різниці виразів 
і 
додатнє?
5. Розв'яжіть нерівність 
і поясніть, які теоретичні положення були при цьому використані.
Варіант 3
1. Обгрунтуйте, чи рівносильні рівняння:
1) 
і 
2) 
і 
3) 
і 
4) 
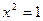і 
2. Знайдіть область визначення та множину розв’язків рівняння
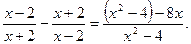
3. Розв’яжіть задачу алгебраїчним способом:
В одному кошику в 3 рази більше яблук, ніж у другому. Якщо у перший кошик покласти 4 яблука, а в другий 6 яблук, то в першому кошику їх стане у два рази більше, ніж у другому. Скільки яблук у кожному кошику?
4. Знайти множину цілих значень 
, які є розв’язком нерівності 
5. Розв'яжіть нерівність 
і поясніть, які теоретичні положення були при цьому використані.
Варіант 4
1. Обгрунтуйте, чи рівносильні рівняння:
1) 
і 
;
2) 
і 
3) 
і 
4) 
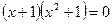і 
2. Знайдіть область визначення та множину розв’язків рівняння
3. Розв’яжіть задачу алгебраїчним способом:
Мати старша за дочку на 21 рік, а 4 роки тому вона була старша від дочки в два рази. Скільки років кожній?
4. Знайти найменше ціле число, яке задовольняє нерівність 
5. Розв'яжіть нерівність 
і поясніть, які теоретичні положення були при цьому використані.
ІV. Підсумок. Домашнє завдання.
1. 
Поняття числової функції
Багато математичних понять виникає в результаті абстрагування від властивостей об’єктів, які реально існують в природі. Відображаючи деякі сторони реальної дійсності, сприяють їх пізнанню.
Одним із понять, яке відображає властивість явищ і предметів і є поняття функції, одне з найважливіших понять математики.
Важливість і складність поняття функції вимагає від початкового курсу математики поступової і систематичної підготовки учнів до засвоєння цього поняття, тобто пропедевтики.
Розглянемо задачу: «Кілограм апельсинів коштує 10 грн. Скільки коштують 3 кг апельсинів? 4 кг? 6 кг апельсинів? Проаналізуємо цю задачу. В задачі мова йде про такі величини, як маса куплених апельсинів, їх вартість і ціна. Якщо позначити через х масу куплених апельсинів, а через у їх вартість, то залежність між ними буде виражатись формулою у=10х. За цією формулою для кожного значення х можна знайти відповідне йому значення у. встановлену залежність у від х називають функцією.
Означення. Функцією називається така залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у.
Змінну х називають незалежною змінною або аргументом, а змінну у - залежною змінною. Кажуть, також, що у є функцією від х.
Щоб задати функцію, треба задати числову множину Х (її називають областю визначення функції) і спосіб (правило), з допомогою якого для кожного числа х із множини Х можна знайти відповідне число у – значення функції.
Функцію прийнято позначати буквами f, g, h та ін. Якщо f- функція, то значення змінної у, відповідає аргументу х, позначають 
, тобто 
.
Найпоширеніші способи завдання функцій такі: аналітичний, табличний та графічний. Частіше всього функції задають за допомогою формул яку вказують, як по даному значенню аргументу знайти відповідне значення функції. Наприклад, якщо довжина сторони квадрата дорівнює х дм, а площина у дм2, то формула у=х2 задає функцію, областю визначенняякої є множина додатних дійсних чисел.
Якщо купили х зошитів, по 3к. кожний, а у к. – ціна всієї покупки, то формула у=3х задає функцію, областю визначення ділення якої є множина цілих невід’ємних чисел.
Іноді функцію задають таким чином:
Тобто на різних ділянках значення х функція задається різними формулами.
Часто при заданні функції за допомогою формули її область визначення не вказується. В таких випадках рахують, що область визначення складається із всіх значеннях змінної, при якій ця формула не має смислу. Наприклад, якщо задана функція 
, то вважають, що її область визначення – множина тих значень х, при яких має смисл вираз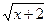 
,тобто множина 
.
Табличний спосіб завдання функції полягає в написанні таблиці відповідних значень аргументу та функції (таблиці кубів, квадратів чисел).
В початковому курсі математики пропедевтика поняття функції здійснюється при заданні таких вправ, в яких розглядаються різні функціональні залежності між змінними. При цьому немає відповідних термінологій, символіки, увага звертається на взаємозв’язки, відношення.
Наведемо приклади декількох завдань:
1. 39+а. Знайти значення суми, якщо а приймає значення: 0, 6, 15, 31, 46, 52.
При розв’язуванні цього завдання встановлюється залежність значення суми 39+а від значень змінної а. Ця залежність – функція з областю визначення 
2. Заповни таблицю:
| b | ||||
| 16 + b |
3. Склади всі можливі приклади на склад однозначних чисел з відповіддю 12.
При виконанні вправи можна скласти таблицю:
За допомогою таблиці встановлюється функціональна залежність значень другого доданка від значення першого. Областю визначення цієї функції є числа 3, 4, 5, 6, 7, 8, 9.
4. Знайди площу квадратів, якщо один квадрат має довжину сторони 1см, другої 2см, третьої 3см.
При розв’язанні цієї задачі встановлюється залежність між довжиною сторони і площею квадрата. Ця залежність – функція, так як кожному значенню довжини сторони квадрата співпадає єдине значення його площі:
- якщо довжина сторони 1см, то площа дорівнює 1см2;
- якщо довжина сторони 2см, то площа дорівнює 4см2;
- якщо довжина сторони 3см, то площа дорівнює 9см2.
Щоб розглянути графічний спосіб завдання функції, розглянемо означення графіка функції.
Графіком функції f, заданій на множині Х, називають множину таких точок координатної площини які мають координати х і f(x) для всіх х із множин Х.
Графіком функції у=х при умові, що областю її визначення є множина дійсних чисел, є множина точок координатної площини, абсциса і ордината яких рівна між собою. Множина таких точок є бісектриса першого і третього координатних кутів. Ця пряма і є графіком функції у=х.
3. Побудуємо графік функції у=х2, рахуючи, що її область визначення є множина дійсних чисел.
Зобразимо кожну пару знайдених значень х і у точкою на координатній площині (мал. 139). Ця лінія називається параболою.
Для аналізу залежності між змінними важливо розуміння суті зростаючої і спадаючої функції.
Функція f називається зростаюча на деякому проміжку Х, якщо для будь-яких значень х1, х2 із множини Х виконується умова 
.
Особливість графіка функції, зростаючому на проміжку Х: при русі вздовж осі Ох зліва направо на проміжку Х ордината графіка збільшується (мал. 140).
Функція f називається спадаючою на деякому проміжку Х, якщо для любих х1, х2 із множини Х виконується умова 
.
Особливість графіка спадаючої на проміжку Х: при русі вздовж осі Ох зліва направо по проміжку Х ордината графіка зменшиться (мал. 141).
Вправи
1. Виміряючи температуру повітря на протязі суток, отримали таку таблицю:
| Х1 | |||||||||||||
| у°С | -2 | -3 | -2 | 3,5 | 3,5 |
Побудуйте графік даної залежності. Чи є вона функцією?
Кожному числу, яке належить множині 
, поставлений належний йому модуль. Покажіть, що дана залежність – функція та побудуйте її графік.
3. Побудуйте графік функції у=х, якщо її областю визначення є множина: 1) 
; 2) 
.
4. Побудуйте графік функції у=2х2, якщо її областю визначення є множина: 1) R; 2) 
; 3) 
.
5. Доведіть, що всі точки графіка функції у=4х2 проходить через точку А(-0,5; -3) і не проходить через точку В(1, -4).
6. Доведіть, що всі точки графіка функції у=102х знаходяться в першій і третій координатній чверті.
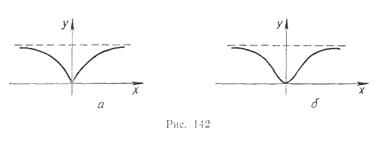
7. В чому ви бачите схожість в поведінці функцій, графіки яких зображені на малюнку 142?
8. Графіки на малюнку 143 розбиті на класи: 
Які властивості відповідних функцій покладені в основу цієї класифікації?
9. Розбийте графіки, наведені на малюнку 144, на три класи, так, щоб графіки а), б), е) опинилися в різних класах. Які властивості даних функцій Ви поклали в основу виконаної класифікації?
10. Формуванню яких представлених про функції і її властивості сприяють наступні вправи які виконуються в початкових класах:
1) Заповни таблицю:
| B | ||||
| 16+b |
|
|
Як змінюються доданки і як змінюється сума?
2) В семи однакових ящиках 42 кг помідорів. Скільки кілограмів помідорів в с таких ящиках? Склади по задачі вираз і знайди його значення при с=6, с=8, с=9, с=10.
3) На лісовій ділянці було 112 беріз і х осин. Обґрунтуй, що означають наступні вирази: 112+х, 112-х, х-112.
Лінійна функція
Якщо учень купив х олівців по 4к. за кожен і зошити по 13 к., то ціна (у к.) його покупки може бути визначена так: у=4х+13. Залежність між кількістю куплених олівців і ціною всієї покупки є функція, так як кожному значенню х відповідає єдине значення у. Ця функція називається лінійною.
Лінійною функцією називається функція, яку можна задати з допомогою формули виду y=kх+b, де х – незалежна змінні, а k і b – задані дійсні числа.
Якщо k=0, то виходить функція виду у=b, її називають постійною функцією.
Областю визначення лінійної функції є множина дійсних чисел. Графіком лінійної функції y=kх+b є пряма. Положення цієї прямої на площині визначають коефіцієнти k і b. Покажемо це.
Роздивимося спочатку графіки функції, заданих формулами 
(мал. 145).
В даних виразах коефіцієнт k приймає різне значення, а коефіцієнт b постійне. Якщо позначити через 
кут між віссю ОХ і графіком лінійної функції і виміряти його проти часової стрілки, то можна побачити, що величина цього кута залежить від коефіцієнта k. Якщо 
, то кут гострий (мал. 146); якщо ж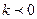 
, то кут тупий (мал. 147). Із малюнка 145 видно, що, чим більше модуль числа k, тим ближче пряма y=kx+b до осі Оу.
|
Так, як коефіцієнт k зв’язаний з кутом , то k називають кутовим коефіцієнтом.
Розглянемо тепер функції, задані формулами у=х+3 та у=х-3 (мал. 148).
|
В них коефіцієнт k один і той же, а коефіцієнт b приймає різне значення, Порівнюючи побудовані на малюнку 148 прямі, підмічаємо, що при зміні b графік переміщується паралельно самому собі. Якщо х=0, то у= b, тобто точка (0, b) належить графіку функції у= k х+ b, тому, коефіцієнт b є значенням довжини відрізка, відтинаючого прямою на осі Оу. Так, для функції у=х+3 та у=х-3 цей відрізок складає 3 одиниці.
Якщо звернути увагу до малюнку 145, то можна побачити, що при k>0 функція у= k х+ b зростає, а при k<0 спадає по всій області визначення. Дійсно, нехай х1<х2. Тоді у1= k х1+ b, у2= k х2+ b. Порівняємо у1 та у2: у2- у1= (k х2+ b)- (k х1+ b)= k(х2-х1).
По умові х2-х1>0, значить знак рівності у2 - у1 залежить від знака коефіцієнта k. Якщо k>0, то у2- у1>0, і поступово, із того, що х1<х2, виходить, що у1 < у2, тобто функція у= k х+ b зростаюча на множині дійсних чисел. Якщо k<0, то у2- у1<0, звідки у1 >у2 та виходячи із того, що х1<х2 виходить, що у1 > у2, тобто функція у= k х+ b спадаюча на множині дійсних чисел.
Вправи
1. Побудуйте графік функції у=2х-3 при умові, що її областю визначення є: а) R; б) 
; в) 
.
2. Відомо, що графік функції у=2х+ b проходить через точку (1,4). Чи пройде вона через точку (3,8)?
3. Знайти коефіцієнти k і b, яка функція задана формулою: а) х-2х=-3; б)2х-3у=-10; в) х-3у=0.
4. Залежність маси (у) ящика з деталями від числа деталей (х) виражається формулою у=0,3х+1,5. Обчисліть масу ящика із деталями при наступних значеннях.
| х | ||||
| у |
Яким буде графік даної залежності?
5. До привалу туристи пройшли 12км. Після привалу вони йшли х годин зі швидкістю 2,5км/год. Складіть формулу, яка виражає залежність між часом руху (х) і всією пройденою відстанню (у). Яку функцію задає ця формула? Яка область визначення даної функції, якщо весь пройдений туристами шлях не перевищує 25 км?
6. Залежність ціни (у) телеграми від числа слів (х) в ній виражається формулою у=5х+20. Обчисліть ціну телеграми при наступних значеннях х:
| х(слів) | ||||
| у(копійок) |
Яка область визначення даної залежності, якщо ціна телеграми не перевищує 1грн. 20к.?
7. Із населеного пункту в місто, яке знаходиться на відстані 20км, зі швидкістю 5км/год відправився пішохід. На якій відстані (s км) від міста буде пішохід через t годин? Які значення може приймати t?
Пряма пропорційність
Якщо t – час руху пішохода (в годинах), s – пройдений ним шлях (в кілометрах) і він рухається рівномірно зі швидкістю 4км/год, то кожному значенню t відповідає єдине значення s, отримане по формулі s=4t. Потім формула s=4 t задає функцію.
Розглянемо ще один приклад. Якщо ціна одного пакета молока 16к., то ціна у (в копійках) х пакетів може бути підрахована так: у=16х. Так як кожному значенню х відповідає єдине значення у, то формула у=16х задає функцію.
В наведених прикладах ми маємо справу з функцією, яку називають прямою пропорційною.
Прямою пропорційністю називається функція, яку може бути задана за допомогою формули виду у=kх, де х – незалежна змінні, а k – не рівне нулю дійсне число.
Число k у формулі у=kх називають коефіцієнтом пропорційності; а про змінну говорять, що вона пропорційна змінній х.
Областю визначення функції у=kх являється множина дійсних чисел.
Пряма пропорційність – частковий випадок лінійної функції у=kх+b, отримане при b=0. Тому:
1) графіком прямої пропорційності являється пряма прохідна через початок координат;
2) k>0 функція у=kх зростає на всій області визначення, а при k<0 спадає.
Наприклад, пряма пропорційність у=2х являється функцією, зростаючою на множині дійсних чисел: якщо значення х зростають, то зростають і значення функції (мал. 149). Функція у=-3х спадаюча на множині дійсних чисел: якщо значення х зростають, то значення функції зменшується (мал. 150).
|
Якщо функція f – пряма пропорційність і (х1, у1), (х2, у2) – пари належних значень х і у, причому х2≠0, то 
. Іншими словами, якщо у= kх, то відношення двох значень змінної х рівне відношенню належних значень у.
Дійсно, якщо f – пряма пропорційність, то вона може бути задана формулою у= kх, і тоді для двох різних значень х1 і х2 маємо, що у1= kх1 і у2= kх2. Так як х2≠0 і k≠0, то у2≠0, то .
Якщо значення змінних х і у є додатні числа, то доведення значення прямої і пропорційності можна сформулювати так:
Із збільшенням (зменшенням) змінної х в декілька раз відповідне значення змінної у збільшується (зменшується) в стільки ж раз.
Пряма пропорційність в початкових класах спеціально не вивчається, але при рішенні текстових задач студенти зустрічаються з різними залежностями між величинами, в тому числі і з прямою пропорційністю. Наведемо приклади таких задач:
1.Метр полотна коштує 4 грн. Скільки коштують 2м полотна?3м?5м? 8м?
В цій задачі розглядається залежність ціни від якості купленого полотна, ціна 1м полотна постійна. Так як ця залежність може бути виражена формулою у=4х, де х – число метрів купленого полотна, а у – його ціна, тоді маємо пряму пропорційність. Коефіцієнт пропорційності 4 заданий в умові задачі, також як і значення, яке приймає х.
2. Із куска тканини довжиною 24м в майстерні пошили 8 однакових костюмів. Скільки потрібно тканини на 20 таких костюмів?
В задачі розглядається залежність витрати тканини від кількості костюмів.
Ця залежність прямо пропорційна, тому може бути задана формулою у=3х, де 3 – кількість метрів тканини для одного костюма, х – число пошитих костюмів, у – кількість тканини, потраченої на ці костюми. Коефіцієнт пропорційності знаходять, знаючи відповідні значення змінних х і у: 24:8=3(м).
Вправи
1. Вкажіть серед наступних функцій, заданих табличним способом, прямі пропорційності:
1)
| х | |||||
| у |
2)
| х | |||||
| у |
3)
| х | |||||
| у | 0,2 | 0,4 | 0,6 | 0,8 |
4)
| х | |||||
| у | -3 | - 
| -9 | - 
| -15 |
2. Побудуйте графіки функцій у=-2х і у=10х і покажіть, що перша із них спадаюча на множині дійсних чисел, а друга зростаюча на тій множині.
3. Обчисліть, яка залежність існує між величинами, даними в задачі і розв’яжіть задачу:
