Этот метод предусматривает движение от точки к точке внутри области допустимых решений одним из градиентных методов. Но при выходе точки за пределы ограничений производится процедура возврата очередного приближения на допустимое множество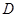 
. Т. е. если была задача
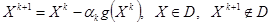
то проекция – ближайшая точка множества 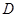, лежит на границе области 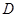. Точка 
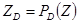называется проекцией точки 
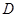на область , если расстояние 
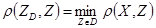. Очевидно, что если точка 
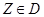, то проекция совпадает с . Таким образом, в методе проекции градиента любая последующая точка вычисляется как:
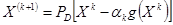
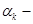коэффициент определяющий длину шага, который определяется так же, как и в методе наискорейшего спуска. Такую задачу можно решить методом «Золотого сечения Ньютона».
Если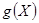 
на множестве 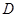удовлетворяет условию Липтица, означающего ограничения но крутизну изменения функции, т. е. 
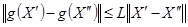, тогда полагают, что 
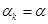, которая выбирается как любое число из интервала 
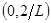если известна минимальная константа Липтица, то 
берут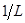 
.
Определение проекции точки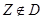 
является самостоятельной задачей НЛП.
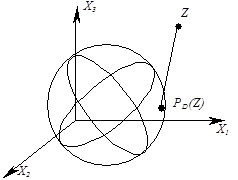
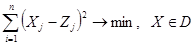
Eсли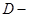 
область определённая линейными ограничениями, то это будет задачей квадратичного программирования. Во многих случаях определение проекции возможно из практических соображений, например, если 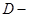шар.
Иногда, как в примере с шаром, нахождение кратчайшего расстояния приводит к задаче на условный экстремум:
 |
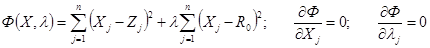В случае с шаром:
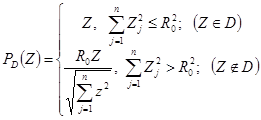
Методы возможных направлений Гаус-Зойтендейка.
В методах возможных направлений переход от точки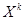 
к точке 
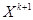осуществляется по направлению 
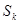, необязательно вдоль градиента. При этом движение вдоль 
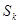должно быть таким, что бы новая точка принадлежала области 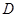. Направление, удовлетворяющее этому условию, называется возможным или допустимым:
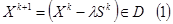
Таких направлений множество; среди возможных направлений выбирают такое, для которого скалярное произведение градиентов в точке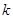 
и этого направления меньше нуля. Такое направление называется подходящим. Таких направлений в общем случае так же множество. Зойтендейк предложил выбирать то, которое максимально уменьшает значение целевой функции:
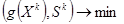
Ограничение нашей задачи
В общем случае, на каждом шаге анализируется не только значение градиентов целевой функции, но и значение градиентов активных ограничений. Активными называются те ограничения, которые находятся вблизи 
ой точки.
В какой-то начальной точке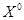 
определяем множество индексов 
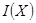, таких что 
. Пусть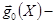 
градиент целевой функции, 
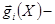градиент функции ограничений, 
номер ограничения. Тогда ищут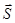 
, такое, что 
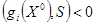. Тогда надо найти 
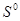, такое, что 
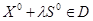. Для этого сначала определяют 
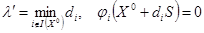, где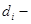 
корень уравнения 
. 
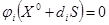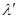выбирается из условия прохода до противоположной границы. Это разумно, когда точка вне области. Затем вычисляется 
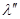, где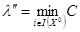 
, здесь 
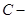корень уравнения 
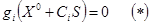. Т. е. 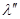определяет длину шага до точки, где градиент равен нулю. Если нет решения выражения (*), то 
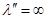, и 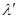выбирается из условия не выхода из области, а 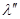выбирается из условия попадания в экстремум.
Кроме этого, при решении вспомогательной задачи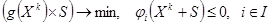 
, используются различные условия нормировки:
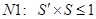
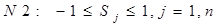
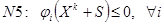– самое распространённое.
Метод Зойтендейка для выпуклой задачи не гарантирует сходимость за конечное число шагов; для квадратичной задачи гарантируется сходимость за конечное число шагов с применением условия сопряжённости градиентов.
Методы экспертных оценок.
Во многих практических задачах при принятии решения возникает принципиальная сложность оценить альтернативы. Например, надо дать оценку качества конкретной физической системы: компьютера, станка. Количество параметров, которые влияют на оценку системы так велико и они настолько разнообразны, что невозможно раз и навсегда задать какой-то способ установки соответствия между качеством системы и числом. В этом случае прибегают к методу экспертных оценок. В этом методе решаются следующие задачи:
· Необходимо построить множество возможных и допустимых альтернатив решения;
· Сформировать набор аспектов, существующих для оценки альтернатив;
· Определяется критериальное пространство;
· Необходимо упорядочить альтернативы по аспектам;
· Получит оценку альтернатив по критериям (отобразить множество допустимых решений в критериальном пространстве.
Все эти задачи – часть общей задачи оценивания – сопоставления числа некоторой альтернативе.
Метод основан на использовании экспертных процедур. Общая схема экспертизы такова: саму оценку выполняют люди, специалисты в предметной области, которые называются экспертами. Для проведения самой экспертизы привлекается консультант. Он определяет множество альтернатив, а иногда и вспомогательное множество для экспертизы. Каждый эксперт выбирает свою оценку и передаёт её консультанту. Эта оценка обрабатывается по очень сложной схеме и получается единая для всех экспертов оценка для каждой альтернативы. Затем по определённому правилу выбирается оптимальная оценка консультантом. В схеме экспертизы заложен блок, который отвечает за оценку согласованности мнения экспертов или оценку компетентности экспертов.
Эксперты могут взаимодействовать друг с другом в одних видах экспертизы, либо наоборот, отделяются друг от друга в других методах. В известном методе экспертизы Делфи, экспертам «вновь» предлагаются результаты экспертизы и просят посмотреть на них и призадуматься. В методе Делфи устанавливается «обратная связь» при экспертизе.
Типы задач оценивания.
Оценивание – составление альтернатив какого-то вектора евклидова пространства.
1) Пусть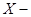 
некоторая альтернатива в множестве альтернатив. 
. Имеется 
критериев, тогда требуется каждой альтернативе сопоставить некоторый вектор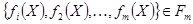 
. Это общая задача оценивания.
2) Пусть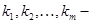 
критерии, учитываемые при выборе. Эти критерии надо установить по возможности, т. е. здесь оценивается система критериев. Система этих критериев сопоставляется перестановке натуральных чисел. Это задачи раипсирования.
3) Пусть некоторое множество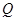 
разбито на 
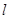подмножеств и для какой-то альтернативы 
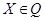необходимо указать, какому подмножеству она принадлежит, т. е. 
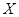сопоставляется конкретное подмножество. Это задача классификации.
4) Пусть 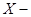отрезок, длину которого надо измерить; т. е. отрезку надо сопоставить действительное число. Это самая простая и самая распространённая задача оценивания.
Обозначим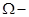 
исходное множество допустимых оценок; 
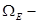множество допустимых оценок для экспертов; 
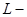тип взаимодействия между экспертами; 
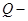наличие обратной связи; 
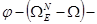алгоритм обработки. Все методы обработки экспертной информации можно разбить на три вида:
1) Статистический метод
2) Алгебраический метод
3) Методы шкалирования.
1) Оценка каждого эксперта рассматривается, как случайная величина. Обработка производится на основе методов математической статистики, которая позволяет определить согласованность методов экспертов и значимость, т. е. качество экспертизы.
Экспертиза 1: численная оценка. Каждой альтернативе ставится в соответствие одно число.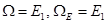 
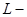; эксперты изолированы; 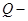обратная связь отсутствует; 
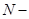количество экспертов:
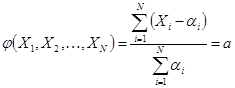
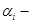веса экспертов; при отсутствии информации компетентности 
; 
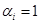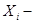числовые оценки экспертов. Степень согласованности определяется выражением:
Дисперсия
Применяется экспертиза.
Экспертиза 2: 
каждый эксперт даёт три оценки для числа:
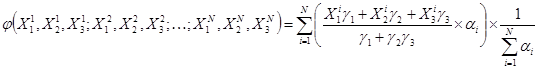
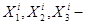соответственно, оптимистическая, наиболее вероятная и пессимистическая оценка эксперта; 
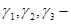веса, которые можно доверять данной оценкой. Обычно 
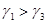и степень согласованности определяется дисперсией:
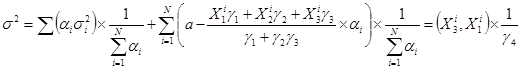
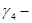коэффициент неуверенности эксперта в своём ответе.
