Игровая модель представляет собой особый вид модели ТПР. До сих пор мы считали, что решение принимается на основе критерия, отражающего эффективность по отношению «к нам». Оказывается, встречается довольно много ситуаций в экономике, особенно в военных операциях, где действует несколько сторон, преследующих различные интересы. И поэтому, невозможно оценить результат принимаемого решения единообразно. Такого рода ситуации называются конфликтными. Теория, описывающая конфликтные ситуации с количественной стороны, называется теорией игр. Интересы между сторонами могут быть полностью противоположными. Такие модели называются антагонистическими играми. Но во многих ситуациях в игре могут принимать участие три и более сторон. Такие игры называются множественными. Некоторые стороны могут объединяться по интересам. Такие игры называются коалиционными.
Игра – модель ситуации, некоторая упрощённая схема, где зафиксированы сами игроки, правила игры, определённые выигрыши после каждого хода, правила окончания игры. В более сложных играх совокупность ходов определяют некоторую стратегию. Мы будем рассматривать только парные игры, в которых есть два игрока, и интересы которых полностью противоположны – антагонистические парные игры. Если игрок 
выиграл 
, то игрок 
выиграл 
(потерял ). Поэтому такие игры называются так же играми с нулевой суммой.
Главным в игровой модели является то, что другая сторона – противник, активно противодействует вам в выборе оптимального решения. Поэтому мы должны объективно оценивать противника, т. е. становиться на его сторону, и считать, что противник не менее разумен чем мы. При этом меняется само понятие оптимального решения. В дальнейшем мы покажем, что принцип согласованного оптимума является основой игры.
Ходы в игре могут быть личные и случайные. Личный ход зависит от сознательного решения стороны, а случайный ход – результат случайного механизма, который иногда применяется специально, а иногда случайно вовлекается в игру.
Например, часто азартные игры состоят из одних случайных ходов. Стратегией игрока называется совокупность правил, определяющих выбор вариантов действий при каждом личном ходе игрока в зависимости от сложившейся ситуации. Если количество стратегий конечно – игра конечная, в противном случае – бесконечная игра.
Задачей теории игр является обоснование оптимальных стратегий обоих игроков. В теории игр считается, что игра повторяется многократно и игроков интересует средний выигрыш. К сожалению, при подходе к выработке оптимального решения приходится применять тот или иной принцип оптимальности.
Платёжная матрица.
Рассмотрим конечную игру в которой у игрока 
стратегий, а у 
. Пусть при применении этих стратегий известен выигрыш 
, тогда говорят, что задана платёжная матрица. Т. е. применение в каждой игре стратегии однозначно определяет исход игры. Если есть случайные ходы, то выигрыш так же случае, и можно взять математическое ожидание выигрыша. Построить матрицу можно не всегда из-за её большого размера (игра в шахматы). Для игр с полной информацией, т. е. когда один игрок знает, как поступил второй, всегда можно построить платёжную матрицу. Рассмотрим простейшие примеры игр:
1) Игра поиск. Игрок прячется в 
первом или втором месте. Игрок ищет его. Если игрок находит , то платит ему один рубль, если же не находит , то платит один рубль . Построим платёжную матрицу.
Решение этой игры: 
.
2) Игра три пальца. 
игроки и одновременно показывают один, два или три пальца. Выигрыш равен сумме, причём если получилось чётное число очков, выигрывает , а если нечётное, то . Строим платёжную матрицу.
Решение у этой игры: 
.
3) 
Игра вооружение – самолёты. У стороны есть три вида вооружения: зенитка, ракета и автомат. У – три типа средств нападения. Известны вероятности, с которыми каждый 
ый тип вооружения сбивает каждое 
ое средство противника . Построим платёжную матрицу.
Решение для этой игры: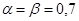 
. Такое решение называется седловой точкой.
Рассмотрим принципы, на основе которых можно обосновать оптимальные решение.
Принцип минимакса.
Рассмотрим игру 
. При анализе игр применяют принцип осторожности (пессимиста). Он требует, чтобы мы больше всего реагировали на плохие ходы со стороны противника (плохие для нас).
Будем рассуждать со стороны игрока : если игрок идет по 
, то мы просматриваем всю строку и фиксируем самую меньшую . И так по всем строкам. 
. После этого мы можем выбрать 
так, чтобы было лучшее из худших: 
– нижняя цена игры (применяя принцип минимакса, меньше величины 
ты не получишь).
Теперь рассмотрим игру со стороны игрока : если игрок рассмотрит столбец 
, то самый худший для него – максимальный в этом столбце. 
. Затем выбираем такую стратегию , которая обеспечивает минимум по максимальным 
: 
верхняя цена игры.
Итак, мы можем сразу найти и 
анализируя матрицы.
Принцип чистых стратегий.
Если игра имеет седловую точку, то говорят, что игра решается в чистых стратегиях. Такое решение обладает свойством устойчивости, т. е. если один игрок придерживается своей оптимальной стратегии, то другому игроку невыгодно отклоняться от своей оптимальной стратегии. Это свойство устойчивости полагается в основу понятия оптимальной игры. В игре может быть несколько седловых точек. Но как правило таких точек нет, и нельзя найти решение в чистых стратегиях.
